Wenn in mehrstimmigen Sätzen mehrere Stimmen neben einander und zugleich melodisch sich bewegen sollen, so wird im Allgemeinen die Regel festgehalten werden müssen, daß dieselben Konsonanzen mit einander bilden müssen. Denn nur wenn sie konsonant sind, findet eine ungestörte Mischung der ihnen entsprechenden Gehörempfindungen statt; sobald sie dissonant werden, stören sich die einzelnen Klänge gegenseitig und hemmen jeder den ungestörten Abfluß des anderen. Zu diesem mehr ästhetischen Motiv kommt noch das andere rein sinnliche, daß die konsonanten Zusammenklänge eine angenehme Art sanfter und gleichmäßiger Erregung der Gehörnerven geben, welche durch größere Mannigfaltigkeit sich von der eines einzelnen Klanges auszeichnet, während die Dissonanzen durch ihre Intermittenzen eine den Gehörnerven quälende und erschöpfende Art der Erregung zu Wege bringen.

Indessen die Regel, daß die verschiedenen Stimmen eines mehrstimmigen Satzes mit einander Konsonanzen zu bilden haben, ist nicht ohne Ausnahme. Das ästhetische Motiv für diese Regel kann nicht dagegen sprechen, daß unter gewissen Bedingungen und für kurze Zeit die verschiedenen Stimmen dissonierend werden, wenn nur übrigens durch die Art der Stimmführung dafür gesorgt ist, daß die Führung der neben einander hergehenden Stimmen durchaas klar bleibe. Es kommen also dann zu dem allgemeinen Gesetze der Tonleiter und Tonart, dem die Führung jeder Stimme unterworfen ist, noch besondere Gesetze für die Führung der Stimmen in dissonanten Akkorden. Ferner kann auch das sinnliche Motiv der größeren Annehmlichkeit der Konsonanzen die Dissonanzen nicht ganz ausschließen. Denn wenn auch das sinnlich Angenehme ein wichtiges Unterstützungsmittel der ästhetischen Schönheit ist, so ist es damit doch nicht identisch. Im Gegenteil brauchen wir in allen Künsten vielfach seinen Gegensatz, das sinnlich Unangenehme, teils um durch den Kontrast die Lieblichkeit des ersteren heller hervorzuheben, teils am einen kräftigeren leidenschaftlichen Ausdruck zu erreichen. In demselben Sinne werden die Dissonanzen in der Musik gebraucht. Teils sind sie Mittel des Kontrastes, am den Eindruck der Konsonanzen hervorzuheben, teils Mittel des Ausdrucks, und zwar nicht bloß für besondere und einzelne Gemütsbewegungen, sondern sie dienen ganz allgemein dazu, den Eindruck des Forttreibens und Vorwärtsdrängens in der musikalischen Bewegung zu verstärken, indem das von Dissonanzen gequälte Ohr sich nach dem ruhigen Dahinfließen des Stromes der Töne in reinen Konsonanzen zurücksehnt. In diesem letzteren Sinne finden sie namentlich unmittelbar vor dem Schlusse eine hervortretende Art der Anwendung, und hier sind sie auch von den alten Meistern der polyphonen Musik des Mittelalters schon regelmäßig gebraucht worden. Aber auch dieser Zweck ihres Gebrauchs fordert, daß die Stimmbewegung so eingeleitet sei, daß der Hörer von vorn herein bemerke, wie die Stimmen einem konsonanten Schlusse zudrängen, der zwar verzögert oder auch vereitelt werden kann, dessen Vorgefühl aber doch das einzige rechtfertigende Motiv für die Existenz der Dissonanzen ist.

Die Zahl der möglichen dissonanten Akkorde wäre unendlich groß, weil alle möglichen irrationalen Tonverhältnisse dissonant sind, und nur die Zahl der Konsonanzen beschränkt ist, wenn nicht die einzelnen Stimmen, welche einen dissonanten Akkord zusammensetzen, aus den angeführten Rücksichten dem Gesetze der melodischen Bewegung folgen, d. h. sich innerhalb der Tonleiter bewegen müßten. Konsonanzen. haben ein selbständiges Recht zu existieren, nach ihnen haben sich unsere modernen Tonleitern gebildet. Dissonanzen aber sind nur als Durchgangspunkte für Konsonanzen erlaubt. Sie haben kein selbständiges Recht der Existenz, und die Stimmen in ihnen bleiben deshalb demselben Gesetze des Fortschritts in den Stufen der Tonleiter unterworfen, welches zu Gunsten der Konsonanzen festgestellt ist.

Indem wir zur Aufzahlung der einzelnen dissonanten Intervalle übergehen, bemerke ich, daß man in der theoretischen Musik gewöhnlich diejenige Lage der dissonanten Akkorde als die normale betrachtet, in welcher ihre einzelnen Töne eine Reihe von Terzen mit einander bilden. Namentlich ist dies die Regel bei den Septimenakkorden, welche aus dem Grundton, dessen Terz, dessen Quinte und dessen Septime bestehen. Die Quinte bildet mit der Terz, die Septime mit der Quinte wiederum ein Terzintervall. So können wir uns die Quinten aus zwei Terzen, die Septimen aus drei Terzen zusammengesetzt denken. Durch Umkehrung der Terzen erhalten wir die Sexten, durch Umkehrung der Quinten die Quarten, durch Umkehrung der Septimen die Sekunden. Wir finden also auf diesem Wege alle in der Tonleiter vorkommenden Intervalle.

Wenn wir die von uns modifizierte Hauptmann'sche Bezeichnungsweise der Töne anwenden, ergibt sich auch leicht, wie die verschiedenen Intervalle gleichen Namens sich in der Größe unterscheiden. Wir müssen nur beachten, daß  um ein Komma höher ist als c, c um zwei Kommata tiefer als , um eines tiefer als c. Ein Komma aber ist etwa der fünfte Teil eines halben Tons.

Um gleichzeitig eine anschauliche Übersicht zu geben, teils über die Größe, teils über die Rauhigkeit der einzelnen dissonanten Intervalle, habe ich die Fig. 61 konstruiert, in welcher die Kurve der Rauhigkeit aus Fig. 60 A (S. 318) kopiert ist. Die Grundlinie X Y bedeutet das Intervall einer Oktave, in welches die einzelnen konsonanten und dissonanten Intervalle nach ihrer Breite in der Skala eingetragen sind. Auf der unteren Seite der Grundlinie sind die zwölf gleichen Halbtöne der temperierten Skale abgeteilt, auf der oberen die konsonanten und dissonanten Intervalle, welche in den natürlichen Tonleitern vorkommen. Die Breite dieser Intervalle ist immer von dem Punkte X bis zu der betreffenden senkrechten Linie hin zu nehmen. Die Lothe, welche den Konsonanzen entsprechen, sind bis zum oberen Rande der Zeichnung verlängert, die der Dissonanzen dagegen kürzer gehalten. Die Höhe dieser Lothe bis zu dem Punkte hin, wo sie die Rauhigkeitskurve schneiden, entspricht der Rauhigkeit, welche der betreffende Zusammenklang, in der Klangfarbe der Violinen ausgeführt, etwa erzeugen würde.

Die verschiedenen Terzen, Quinten und Septimen der Tonart finden wir, wenn wir die Töne der Leiter nach Terzen ordnen.

                                                                                       H   —   d   |  f   —   a   —   c   —   c   —   g   —   h   —   d   |  f   —   a
                                                                                                                            ^6/₅      ³²/₂₇   ⁵/₄       ⁶/₅       ⁵/₄       ⁶/₅        ⁵/₄        ⁶/₅    ³²/₂₇  ⁵/₄

                                                                                     H  —    d    |  f   —    —   c   —    —   g   —   h   —   d   |  f   —   as
                                                                                                                        ⁶/₅       ³²/₂₇    ⁶/₅         ⁵/₄         ⁶/₅         ⁵/₄        ⁵/₄      ⁶/₅    ³²/₂₇   ⁶/₅.

In der natürlichen Dur- und Molltonleiter kommen, wie man in der obigen Aufstellung sieht, dreierlei Arten von Terzen vor, welche umgekehrt eben so viele Arten von Sexten geben, nämlich:

l) Die natürliche große Terz ⁵/₄ und ihre Umkehrung, die kleine Sexte ⁸/₅ beide konsonant.

2) Die natürliche kleine Terz ⁶/₅ und ihre Umkehrung, die große Sexte ⁵/₃ ebenfalls beide konsonant.

3) Die Pythagoräische kleine Terz ³²/₂₇ zwischen den Grenztönen der Tonart d und f. Führte man die Stimmung d statt d ein, so würde dasselbe Intervall sich zwischen h und d zeigen. Vergleicht man diese dissonante Terz d — f mit der konsonanten kleinen Terz d — f der Größe nach, so ist erstere um ein Komma enger als letztere, da d um ein Komma höher als d ist. Die Pythagoräische kleine Terz steht der natürlichen kleinen Terz an Wohlklang etwas nach, aber ihr Unterschied in dieser Beziehung ist nicht so groß, wie der der entsprechenden beiden großen Terzen. Der Unterschied beruht einmal darin, daß die große Terz eine vollkommenere Konsonanz ist als die kleine Terz, und jener Verstimmung daher mehr schadet, als dieser. Dann findet sich aber auch in den Kombinationstönen ein Unterschied. Die reine kleine Terz d"' — f "' bildet den Kombinationston b, ergänzt sich also zum reinen B-Dur-Dreiklange. Die Pythagoräische Terz d'" — f '" gibt den Kombinationston a, ergänzt sich also zu dem Akkorde d — f — a, der kein ganz richtiger Mollakkord ist. Da aber die unrichtige Quinte a nur schwach in den tiefen Kombinationstönen liegt, merkt man den Unterschied kaum. Außerdem ist es auch praktisch fast unmöglich, das Intervall so genau zu stimmen, daß der Kombinationston a und nicht a wird. Bei der Pythagoräischen großen Terz c" — e" ist aber der Kombinationston cis, was natürlich viel störender ist, als die nicht ganz reine Quinte a bei dem Zusammenklänge d — f.

Die Pythagoräische große Terz kommt in den von der harmonischen Musik geforderten Stimmungen der Tonleitern nicht vor. Wenn man in der Molltonleiter die kleine Septime b statt  benutzen wollte, würde b — d eine solche Terz sein.

Die Umkehrung der Terz d — f ist die Pythagoräische große Sexte f — d, ²⁷/₁₆ um ein Komma größer als die natürliche große Sexte, der sie an Wohlklang sehr bedeutend nachsteht, wie Fig. 61 deutlich zeigt.

Die Quinten setzen sich einfach aus je 2 Terzen zusammen; je nach der Art der Terzen, welche wir zusammensetzen, erhalten wir die verschiedenen Arten der Quinten.

4) Die reine Quinte ³/₂, bestehend aus einer natürlichen großen und einer eben solchen kleinen Terz. Ihre Umkehrung ist die reine Quarte ⁴/₃ beide sind konsonant. Beispiele in der Durtonleiter: f — c, a — e, c — g, e — h, g — d.

5) Die unreine Quinte d — a, ⁴⁰/₂₇, um ein Komma kleiner als die reine Quinte d — a, besteht aus der großen und der Pythagoräischen kleinen Terz. Sie klingt wie eine schlecht gestimmte Quinte, und macht deutlich zu unterscheidende Schläge. In der eingestrichenen Oktave ist die Zahl dieser Schläge 11 in der Sekunde. Ihre Umkehrung ist die unreine Quarte a — d, ²⁷/₂₀, welche ebenfalls entschieden dissonant ist. Die Quarte a — d macht eben so viel Schläge wie die Quinte d — a', wenn in beiden der Ton d der gleiche ist.

6) Die falsche Quinte h — f, ⁶⁴/₄₅, besteht aus einer natürlichen und einer Pythagoräischen kleinen Terz h — d und d — f, und ist deshalb, wie die Notenschrift schon andeutet, um etwa einen halben Ton kleiner als die reine Quinte. Sie ist eine ziemlich rauhe Dissonanz, an Rauhigkeit etwa der großen Secunde gleichstehend. Ihre Umkehrung, die falsche Quarte oder der Tritonus, f — h (drei Ganztöne umfassend f — g, g — a, a — h),⁴⁵/₃₂, ist ihr an Rauhigkeit nahe gleich, und etwa um ein Komma kleiner. Nämlich nahehin ist die falsche Quinte h — f gleich ces — f, und wenn man dieses Intervall um ein Komma kleiner macht, erhält man ces — f, welches eine falsche Quarte ist. Genau genommen, da ces nicht vollkommen gleich ist mit h, ist der Unterschied zwischen beiden Intervallen etwas kleiner als ein Komma, ⁸¹/₈₀, nämlich ²⁰⁴⁸/₂₀₂₅ oder abgekürzt ⁸⁹/₈₈. Auf den Tasteninstrumenten fallen beide zusammen.

7) Die übermäßige Quinte der Molltonart  — h, ²⁵/₁₆, besteht aus zwei großen Terzen  — g und g — h. Sie ist nahehin um zwei Kommata kleiner als die kleine Sexte, wie man sieht, wenn man statt h das nahehin gleich hohe ces setzt. Es ist  — h also gleich  — ces, die konsonante kleine Sexte ist aber es — ces und  ist um zwei Kommata höher als es. Die übermäßige Qninte ist merklich rauher als die natürliche kleine Sexte, mit der sie auf den Tasteninstrumenten zusammenfällt. Das umgekehrte Intervall, die verminderte Quarte h — , ³²/₂₅, ist dem entsprechend um zwei Kommata höher als die natürliche große Terz, und beträchtlich rauher als diese, fällt aber auf den Tasteninstrumenten mit ihr zusammen.

Zwei natürliche kleine Terzen oder zwei Pythagoräische kommen in der natürlichen Terzenfolge der Dur- und Molltonleiter nicht neben einander zu stehen. Im Septimen- und Quartengeschlecht können allerdings die Intervalle a —  und e —, ³⁶/₂₅, sich bilden, aus je zwei natürlichen kleinen Terzen zusammengesetzt; diese sind um ein Komma größer als die gewöhnlichen fälschen Quinten h — f’ (oder a — es in b-Dur, e — b in f-Dur), und sind merklich rauher als diese.

Je drei Terzen zusammengefaßt geben Septimen; von den kleinsten anfangend, erhalten wir folgende verschiedene Größen derselben: Die verminderte Septime der Molltonart h —  == (h — d') + (d' — f' ) + (f ' — ), zwei natürliche und eine Pythagoräische kleine Terz umfassend. Ihr Zahlenverhältnis ist ¹²⁸/₇₅, sie ist um etwa zwei Kommata größer als die große Sexte, wie man sieht, wenn man setzt h —  == ces — . Das Intervall ces — , welches um zwei Kommata enger ist, würde eine reine große Sexte sein. Ihre Dissonanz ist ziemlich scharf und rauh, ähnlich der der Pythagoräischen großen Sexte, welche um ein Komma kleiner ist. Ihre Umkehrung dagegen, die übermäßige Secunde—h, ist nicht viel rauher als die natürliche kleine Terz. Ihr Zahlenverhältnis ⁷⁵/₆₄ ist sehr nahe dem Verhältnis ⁷/₆ gleich . Erweitert man diese Secunde zur None ⁷/₃, so wird sie ziemlich wohlklingend, ungefähr so wie die allerdings recht unvollkommene Konsonanz der kleinen Decime ¹²/₅.

9) Die engere kleine Septime g —f', h — a' oder d — c, ¹⁶/₉, besteht aus einer großen, einer natürlichen und einer Pythagoräischen kleinen Terz, g — f ' == (g — h) + (h — d') + (d' — f' ). Sie ist eine verhältnismäßig milde Dissonanz, milder als die verminderte Septime, was für die Wirkung des Dominantseptimenakkordes, in welchem diese Septime vorkommt, von Wichtigkeit ist. Es ist diese engere kleine Septime von allen Septimenintervallen der natürlichen Septime ⁷/₄ am nächsten, doch nicht so nahe, wie das später zu erwähnende Intervall der übermäßigen Sexte. Daß sich die natürliche Septime im Wohlklang den Konsonanzen anschließt, habe ich schon früher erörtert. Die Umkehrung dieser Septime ist der große Ganzton c — d, a — h, f — g, ⁹/₈, der eine kräftige Dissonanz bildet.

10) Die weitere kleine Septime e — d', a — g',⁹/₅, um ein Komma größer als die vorige, klingt merklich schärfer, weil sie sich der Oktave mehr nähert; sie ist der verminderten Septime an Rauhigkeit fast gleich. Sie besteht aus einer großen und zwei natürlichen kleinen Terzen; e — d' = (e — g) + (g — h) + (h — d'). Die vorher genannte engere kleine Septime muß ihren Grundton auf der Oberdominantseite, ihre Septime auf der Unterdominantseite der Tonart haben, weil sie die Pythagoräische Terz d — f in ihre Grenzen einfaßt. Die weitere kleine Septime hat umgekehrt ihre Septime auf der Oberdominantseite. Ihre Umkehrung, der kleine Ganzton, ¹⁰/₉ d — e, g — a, ist etwas schärfer im Zusammenklange, als der große Ganzton.

11) Die große Septime f— e', c — h,¹⁵/₈, besteht aus zwei großen und einer natürlichen kleinen Terz c — h == (c — e) + (e — g) + (g — h). Sie ist eine scharfe Dissonanz, etwa eben so scharf, wie der kleinere Ganzton. Ihre Umkehrung, die kleine Secunde oder der Halbton ¹⁶/₁₅ ist von allen Dissonanzen der Tonleiter die schärfste.

Eine etwas abweichende große Septime könnte im Quarten- oder Septimengeschlecht entstehen, — a', welche um ein Komma kleiner wäre als die gewöhnliche große Septime, und deshalb im Klange etwas milder.

Zu erwähnen ist endlich noch ein eigentümliches Intervall des dorischen Sextengeschlechts, nämlich

12. Die übermäßige Sexte — h, welche durch Verbindung der diesem Geschlechte eigentümlichen kleinen Secunde  mit dem Leittone h entsteht. Der Wert des Intervalls ist ²²⁵/₁₂₈; es ist um etwa ein Komma kleiner als die kleine Septime des Dominantseptimenakkordes, wie man sieht, wenn man setzt  — h ==  — ces'; eine engere kleine Septime würde des — ces' sein;  ist aber ein Komma höher als des. Man kann die übermäßige Sexte zusammengesetzt denken aus zwei großen Terzen und einem ganzen Ton:

Ihr Wohlklang ist dem der kleinen Sexte gleich, weil sie nämlich fast genau dem natürlichen Intervalle ⁷/₄ entspricht. Es ist nämlich . Sie kann also allein genommen nicht als Dissonanz betrachtet werden, aber sie läßt. keine anderen konsonanten Verbindungen zu, und kann also nicht konsonante Akkorde bilden. Wenn sie umgekehrt wird, in die verminderte Terz ²⁵⁶/₂₂₅ oder annähernd ⁸/₇, so verschlechtert sie sich bedeutend, wie schon früher bemerkt wurde; dagegen verbessert sie sich, wenn der höhere Ton h eine Oktave höher gelegt wird, wo sie nahehin das Intervall ⁷/₂ darstellt. Die nahe Übereinstimmung mit der natürlichen Septime und der verhältnismäßige Wohlklang scheint es zu sein, der dieses sonderbare und unserem jetzigen Tonsystem widersprechende Intervall in den Cadenzen erhalten hat, und charakteristisch ist es hierfür, daß seine Umkehrung in die verminderte Terz, welche den Wohlklang vermindert, verboten ist, wohl aber die Erweiterung in die entsprechende Terzdezime erlaubt ist. Auf den Tastaturinstrumenten fällt dieses Intervall mit der kleinen Septime zusammen.

Überhaupt wird ein Blick auf die Fig. 61 lehren, wie außerordentlich verschiedene Intervalle auf den Tastaturinstrumenten verschmolzen werden. Auf der unteren Seite der Grundlinie X — Y sind die Orte der Töne der gleichschwebenden Temperatur angegeben, und die kleinen Klammern längs der Linie X Y umfassen diejenigen Tonstufen, welche durch den entsprechenden Ton der temperierten Skala ausgedrückt zu werden pflegen. Das Intervall h — wird auf dem Klaviere ebenso gegriffen wie eine große Sexte ces — as, das Intervall  — h dagegen wird um einen halben Ton weiter gegriffen, und doch ist das letztere vom ersten kaum mehr unterschieden, als das erste von der großen Sexte. Und namentlich zeigt die Figur auch sehr gut, welcher große Unterschied in dem Wohlklange zwischen dem Intervalle c — a und dem f — d' oder h — ' bestehen sollte, während diese alle durch den ziemlich scharfen Klang des temperierten Intervalls c — a ausgedrückt werden. Das Harmonium mit doppelter Tonreihe erlaubt dagegen, alle diese Intervalle rein zu greifen, wobei die Unterschiede ihres Klanges äußerst auffallend sind. Hierin liegt offenbar eine der größten Unvollkommenheiten der temperierten Stimmung.

Dissonante Dreiklänge mit je einer Dissonanz erhalten wir, wenn wir zu demselben Grundtone je zwei Konsonanzen hinzusetzen, die mit einander aber dissonant sind. Also

1) Quinte und Quarte: c — f — g.

2) Terz und Quarte: c — e — f oder c —  — f.

3) Quinte und Sexte: c — g — a oder c — g — .

4) Ungleichartige Terz und Sexte: c —  — a oder c — e — .

In allen diesen ist c zu beiden anderen Tönen konsonant. Nur der erstgenannte Akkord spielt namentlich in der älteren polyphonen Musik als sogenannter Vorhaltsakkord eine wichtige Rolle. Die übrigen werden wir später als Teile von Septimenakkorden wiederfinden.

Die unter 4 genannten Akkorde können eine Umlagerung erfahren, wobei sie als Dreiklänge mit verminderten oder übermäßigen Quinten erscheinen, nämlich:

Der erste derselben ist aus zwei reinen kleinen Terzen zusammengesetzt, der zweite aus zwei reinen großen Terzen; beide sind wegen der veränderten Quinte dissonant, obgleich die Dissonanz des zweiten auf den Tastaturinstrumenten wie die Konsonanz gis — e gegriffen wird. Der erste beider Akkorde kann nur im Terzengeschlecht vorkommen, der obige würde in das von F gehören; der zweite dagegen gehört zu F-Moll.

Denken wir uns die Reihe dieser Töne fortgesetzt

   —   c'   —   e'   —    —   c"   —   e",
           ⁵/₄          ⁵/₄        ³²/₂₅        ⁵/₄        ⁵/₄

ein, welches ein wenig (nahehin zwei Kommata) größer ist als eine reine große Terz. Durch kleine Änderungen der Tonhöhe bilden sich andere Akkorde, die anderen Tonarten angehören:

   —   c   —   e   —   in F-Moll
            ⁵/₄           ⁵/₄         ³²/₂₅      —   c   —   e   —    in A-Moll
             ³²/₂₅      ⁵/₄         ⁵/₄      —   c   —      —   in -Moll.
              ⁵/₄        ³²/₂₅          ⁵/₄   Die Grundtöne dieser drei Molltonarten — F — A

Wichtiger sind in der neueren Musik die Dreiklänge mit zweiDissonanzen, welche die Grenztöne der Tonart zusammenfassen.

In dem Akkordsystem der Tonart folgen sich wechselnd große und kleine Terzen, von denen zwei benachbarte zusammengefaßt konsonante Dreiklänge geben. Zwischen den Grenztönen d und f aber beträgt das Intervall eine Pythagoräische kleine Terz, und wenn diese mit einer der nächstanschließenden Terzen zu einem Dreiklange vereinigt wird, wird dieser dissonant:

Das Dursystem gibt zwei Dreiklänge der Art:  
h   —   d   —   f   und   d   —   f   —   a,
        ⁶/₅       ³²/₂₇                 ³²/₂₇     ⁵/₄,

h — d — f und d — f — 
      ⁶/₅   ³²/₂₇        ³²/₂₇  ⁶/₅

d — f — ,

d — ,

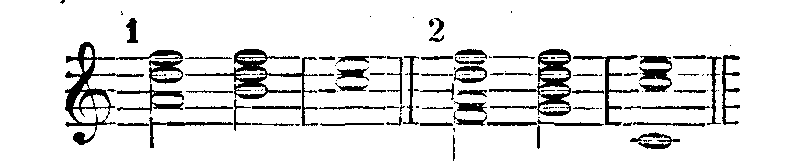
Diese Akkorde, und zwar am entschiedensten und deutlichsten der Akkord h — d — f, haben nun noch für die Musik die besondere Wichtigkeit, daß sie die Grenztöne der Tonart, durch welche diese von den nächstverwandten geschieden ist, zusammenfassen, und somit sehr bestimmt die Tonart bezeichnen, in welcher sich die Harmonie zur Zeit bewegt. Schritte sie nach G-Dur oder G-Moll fort, so würde statt des f ein fis eintreten müssen. Schritte sie nach F-Dur fort, so würde statt d ein d oder in F- Moll ein  eintreten. Außerdem würde sich in dem h enthaltenden Akkorde ein b einstellen. Also:

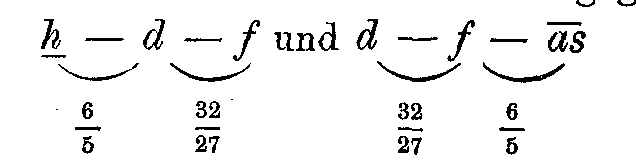
leicht verwechselt werden mit

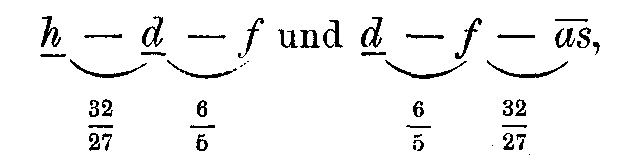
von denen der erstere zu a-Moll und der letztere zu -Dur oder -Moll gehört. a-Moll ist die dem c-Dur nächstverwandte Molltonart, -Dur die dem c-Moll nächstverwandte Durtonart.

Und endlich, wenn man berücksichtigt, daß die kleine Pythagoräische Terz ³²/₂₇ noch weniger von der übermäßigen Secunde ⁷⁵/₆₄ geschieden ist, als von der normalen kleinen Terz (³²/₂₇ == ⁶/₅× ⁸⁰/₈₁ und ³²/₂₇ == ⁷⁵/₆₄ × ²⁰⁴⁸/₂₀₂₅ oder nahehin ³²/₂₇ == ⁷⁵/₆₄× ⁸⁹/₈₈), so kann der Dreiklang h — d — f durch verhältnismäßig kleine Änderungen der Intonation übergehen in

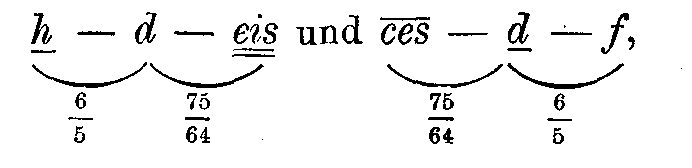
die zu fis-Moll und es-Moll gehören. Es kann also der verminderte Dreiklang h — d — f bei Änderungen seiner Intonation um nur ⁸¹/₈₀ zu den Tonarten

Konsonante vierstimmige Akkorde lassen sich nicht bauen, wie früher gezeigt ist, ohne einen der Töne in der Oktave zu verdoppeln, aber dissonante Akkorde lassen sich vierstimmig bauen. Die am wenigsten dissonante Art dieser Akkorde ist diejenige, wo nur ein einziges Intervall dissonant ist, alle übrigen konsonant. Man bildet sie am einfachsten, wenn man zwei konsonante Dreiklänge vereinigt, die je zwei gemeinsame Töne enthalten. Bei der Vereinigung sind dann die nicht gemeinsamen Töne dissonant, alles übrige ist konsonant, so daß die Dissonanz zwischen der Menge der übrigen konsonanten Töne sich verhältnismäßig wenig bemerkbar macht. Also die Akkorde

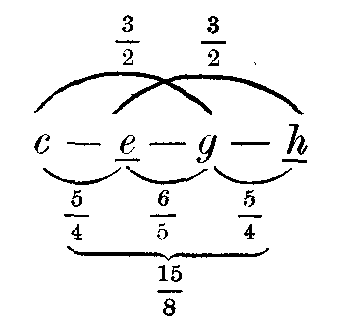
Diese aus der engsten Lage der Dreiklänge abgeleitete Lage des Septimenakkords wird als die fundamentale Lage desselben betrachtet. Die Intervalle zwischen den einzelnen Tönen erscheinen als Terzen, und wenn wir die Septimenakkorde aus den konsonanten Dreiklängen der Tonleiter bilden, müssen diese Terzen abwechselnd große und kleine sein, weil in den konsonanten Dreiklängen immer eine große Terz mit einer kleinen vereinigt ist. Hauptmann nennt diese Septimenakkorde, welche in der natürlichen Terzenfolge der Tonart

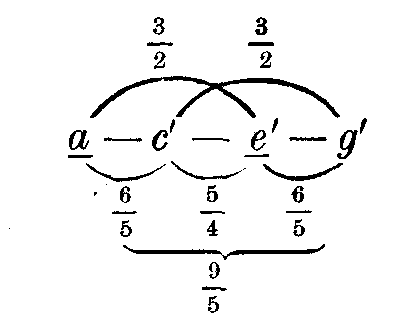
und dem ähnlichen Dreiklange e — g — h — d aus der C-Durleiter und f —  — c —  aus C-Moll. Diese letzteren haben als Dissonanz die kleine Septime, welche viel milder ist als die Dissonanz der großen Septime.

c —  — g — h — d   ½  f —  — c

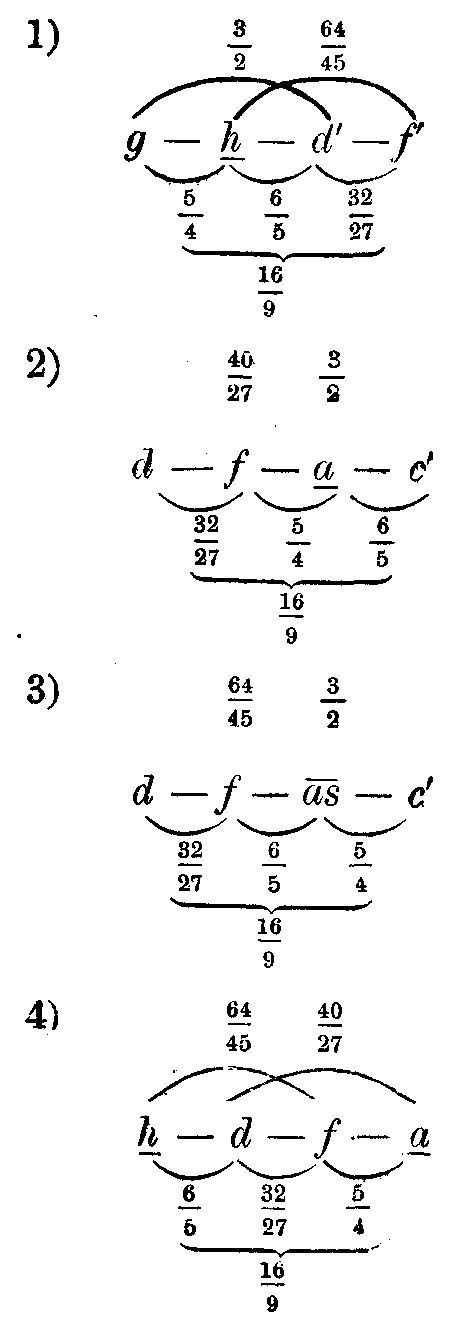
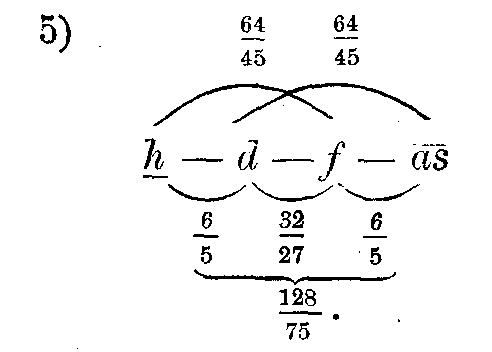
Die Septimen in diesen Akkorden, welche alle der natürlichen Septime — ziemlich nahe kommen, sind sämtlich kleiner als die der aus konsonanten Akkorden zusammengesetzten Septimenakkorde. Die Hauptdissonanzen dieser Akkorde sind die falschen und unreinen Quinten h — f, d — a und d — , also die Intervalle ⁶⁴/₄₅ und ⁴⁰/₂₇. Die drei ersten Septimenakkorde g — h — d — f, d — f — a — c und d — f —  — c, welche nur je eine dieser unreinen Quinten enthalten, sind deshalb milder dissonant als die beiden letzten mit je zwei unreinen Quinten. Unter diesen Akkorden stehen die, welche einen Durakkord enthalten, nämlich

Der Septimenakkord dagegen, welcher eine falsche Quinte und einen Mollakkord enthält,

schließt sich in der Rauhigkeit den Akkorden des unverwendeten Systems mit großer Septime an:

Dabei ist auffallend, daß der genannte Akkord genau dieselben Intervalle, nur in umgekehrter Lage hat wie g — h — d — f,
denn

Auch hier ist der Grund wieder in den Kombinationstönen zu suchen, von denen die tief liegenden der engeren Intervalle am deutlichsten sind. Diese sind für
 
 

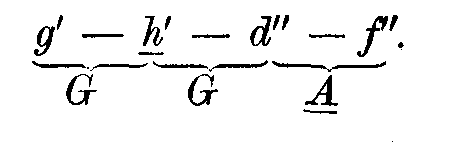
und für

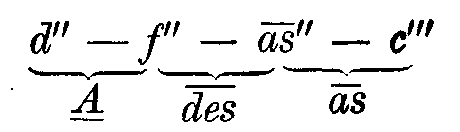
Der erstere enthält unter den angegebenen Kombinationstönen nur einen, der zum Akkorde nicht paßt, der zweite zwei.

Die rauhesten sind die Septimenakkorde mit je zwei falschen Quinten, h — d — f' — a' und h — d' — f' —', von denen der erstere aber wieder mittels einer kleinen Änderung seiner Stimmung ziemlich weich gemacht werden kann. Wenn man nämlich angibt h — d — f' — a', so enthält der Akkord lauter Töne des G-Klanges, und diese klingen ziemlich gut zu einander.

Die Akkorde des verwendeten Systems spielen nun eine wichtige Rolle in modulatorischen Bewegungen, um die Tonart fortdauernd genau zu bezeichnen. Am entschiedensten wirkt in dieser Beziehung der Septimenakkord auf der Dominante der Tonart, also für die Tonica C der Akkord g — h — d — f. Wir sahen, daß der verminderte Dreiklang h — d — f durch kleine Änderungen der Intonation angepaßt werden kann den Tonarten

Von diesen enthalten aber nur die beiden ersten noch den Ton G, so daß der Akkord g — h — d — f nur der Tonica C angehört.

Der unreine Molldreiklang d — f — a, welcher bei genauer Intonation nur der C-Durleiter angehört, ließ die Verwechselung mit d — f — a zu, welcher zu A-Moll, F-Dur und B-Dur gehören kann. Durch die Hinzufügung des Tones C wird diesen Verwechselungen nicht vorgebeugt, so daß der Septimenakkord d — f — a — c nur in Abwechselung mit dem Dominantseptimenakkorde in der Kadenz gebraucht zu werden pflegt, wo er dann G-Dur von C-Moll unterscheidet. Wohl aber ist die Hinzufügung des Tones h zu dem Dreiklange d — f — a charakteristisch, weil dieser höchstens noch die Verwechselung mit dem Akkorde h — d —f — a, der zu A-Moll gehört, zuläßt. Der Akkord h — d —f — a, zwischen Durakkorden gebraucht, klingt aber verhältnismäßig rauh, namentlich in jeder Umlagerung, in der a nicht der oberste Ton bleibt, und findet deshalb nur eine beschränkte Anwendung. Oft wird er mit dem Dominantseptimenakkorde vereinigt, als Nonenakkord g — h — d' — f ' — a', wo aber g und a' seine äußersten Töne bleiben müssen. Darüber unten mehr.

In der C-Molltonart kann der Dreiklang d — f — , der in seiner reinen Intonation an sich charakteristisch wäre, auch mit anderen leicht vertauscht werden. Es gehört:

d — f —  zu C-Moll
   ³²/₂₇ ⁶/₅   d — f — as zu Es-Dur und Es-Moll
      ⁶/₅ ³²/₂₇   d —  — gis zu A-Moll
     ⁶/₅ ⁷⁵/₆₄   — eis — gis zu Fis-Moll.
      ⁷⁵/₆₄    ⁶/₅  

d — f —  — c

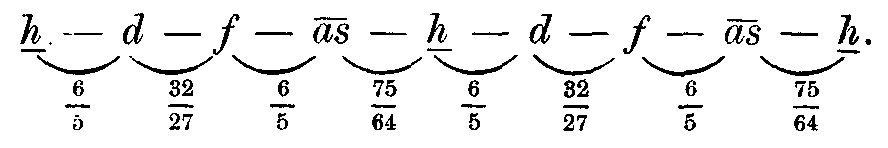
Da die drei Intervalle ⁶/₅, ³²/₂₇und ⁷⁵/₆₄ nur sehr wenig verschieden sind, so können sie leicht mit einander verwechselt werden, und wir erhalten folgende Tonreihen, die nahe gleich sind:

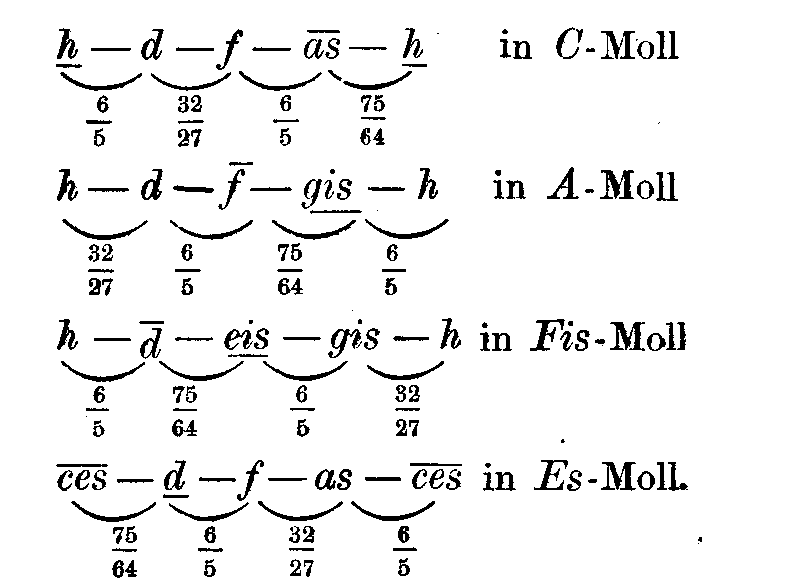
Diese verminderten Septimenakkorde stechen in der Molltonart nicht so scharf gegen die konsonanten Akkorde ab, wie der entsprechende Akkord in der Durtonart, obgleich sie bei reiner Stimmung immer eine sehr einschneidende Dissonanz geben. Wenn sie gefolgt werden von dem Dreiklange der Tonica, so enthalten diese beiden Akkorde zusammen sämtliche Töne der Tonart, bezeichnen diese also sehr vollständig. Die Hauptverwendung findet übrigens der verminderte Septimenakkord durch seine Veränderlichkeit, um schnell in eine neue entferntere Tonart überzuleiten. Durch bloße Hinzufügung des Molldreiklanges von Fis-, A-, C- oder Es-Moll wird dann diese neue Tonart selbst ganz vollständig festgestellt. Man bemerkt leicht, daß die Reihe dieser Tonarten selbst einen verminderten Septimenakkord bildet, dessen Töne um einen halben Ton höher liegen als die des angegebenen Akkordes. Dadurch sind die Tonarten, zu denen er gehört, leicht zu merken.

Das Zusammenschließen der Tonart durch diese Akkorde ist besonders wichtig in der Kadenz am Schlusse einer Komposition, oder einer Hauptperiode derselben. Dazu müssen wir nun noch feststellen, welche Grundklänge durch die hierher gehörigen Septimenakkorde repräsentiert werden können.

In dieser Beziehung ist aber zu bemerken, daß die Töne eines dissonanten Akkordes nie alle, oder dann wenigstens nur unvollkommen, einen einzigen Klang repräsentieren; einige von ihnen kann man aber in der Regel als Bestandteile eines Klanges auffassen. Dadurch entsteht ein praktisch wichtiger Unterschied zwischen den verschiedenen Tönen eines solchen Akkordes. Diejenigen Töne nämlich, welche als Bestandteile eines Klanges zusammengefaßt werden können, bilden mit einander eine in sich geschlossene und zusammengehörige Klangmasse. Ein oder zwei andere Töne des Akkordes dagegen, welche in diese Klangmasse nicht hineingehören, erscheinen als vereinzelte und zufällig nebenher laufende Töne. Diese letzteren werden von den Musikern die Dissonanzen oder die dissonanten Noten des Akkordes genannt. An und für sich ist in einem dissonanten Intervall der eine Ton natürlich ebenso gut dissonant gegen den anderen, wie der zweite gegen den ersten, und wenn keine anderen hinzukommen, hat es keinen Sinn, nur einen von ihnen allein für die dissonante Note erklären zu wollen. In der Septime c — h z. B. ist c gegen h und h gegen c dissonant, jedes nur in Beziehung auf das andere. In dem Akkorde c — e — g— h dagegen bildet c — e — g eine einzige Klangmasse, die dem Klange des C entspricht, und h ist ein vereinzelt nebenher gehender Ton. Die drei Töne c — e — g treten deshalb mit selbständiger Sicherheit auf, sich gegenseitig unterstützend und haltend. Die vereinzelte Septime h dagegen muß sich ohne Unterstützung gegen die Übermacht der anderen halten, was sie sowohl in der Aasführung durch den Sänger, wie im Verständnis des Hörers, nur kann, wenn ihr melodischer Fortschritt sehr einfach und leicht verständlich gehalten ist. Deshalb sind für diese eine Note besondere Regeln der Stimmführung zu beobachten, während der Einsatz des c, welches seine hinreichende Sicherheit in dem Akkorde selbst findet, ganz frei und ungehindert erfolgt. Dieser praktische Unterschied in den Gesetzen der Stimmführung wird von den Musikern dadurch ausgedrückt, daß sie in diesem Falle h allein als den dissonanten Ton des Akkordes bezeichnen. Wenn auch diese Bezeichnung nicht gerade sehr passend gewählt ist, so können wir sie doch ferner unbedenklich gebrauchen, nachdem wir hier auseinandergesetzt haben, was ihr eigentlicher Sinn ist.

Wir gehen nun dazu über, für die einzelnen von uns gefundenen Septimenakkorde festzustellen, welchen Klang sie vertreten, und welches ihre dissonanten Töne sind.

l. Der Dominantseptimenakkord g — h — d — f enthält drei Töne, welche dem Klange G angehören, nämlich g, h und d, während die Septime f der dissonante Ton ist. Indessen ist zu bemerken, daß diese kleine Septime g — f dem Verhältnis 4:7, welches fast genau durch das Intervall g — f hergestellt wäre, schon so nahe liegt, daß der Ton f allenfalls als siebenter Partialton des Klanges G gelten kann. Genauer wäre dieser Klang darzustellen durch g — h — d — f. Sänger wandeln auch wohl leicht das f des Septimenakkordes in f um, teils weil es in der Regel nach unten auf e fortschreitet, teils weil sie durch diese Umwandlung einen milder klingenden Akkord erzielen. Das wird namentlich leicht geschehen, wenn in dem vorausgegangenen Akkorde der Klang des f nicht mittels einer nahen Verwandtschaft festgestellt ist. Also z. B. wenn zu dem schon liegenden konsonanten Akkorde g — h — d später noch ein f hinzutreten soll, wird dieses leicht ein f werden, weil f mit keinem der Töne g, h oderd nahe verwandt ist. Trotzdem also der Dominantseptimenakkord ein dissonanter Akkord ist, so liegt doch selbst sein dissonanter Ton dem entsprechenden Partialton im Klange der Dominante so nahe, daß der ganze Akkord sehr wohl als Vertreter des Klanges der Dominante angesehen werden kann. Eben deshalb ist denn auch die Septime dieses Akkordes von manchen Beschränkungen der Stimmführung befreit, denen man die dissonanten Septimen sonst unterwirft. Man erlaubt namentlich, daß sie frei und sprungweise einsetzen darf, was in anderen Fällen nicht erlaubt ist. In modernen Kompositionen (Richard Wagner) tritt auch nicht ganz selten ein Septimenakkord als Schlußakkord untergeordneter Abschnitte des Satzes ein.

Der Dominantseptimenakkord spielt in der neueren Musik deshalb nächst dem tonischen Akkorde die wichtigste Rolle. Er bezeichnet genau die Tonart, genauer als der einfache Dreiklang der Dominante g — h — d und genauer als der verminderte Dreiklang h — d — f. Als Dissonanzakkord drängt er zur Auflösung in den tonischen Akkord, was der einfache Dreiklang der Dominante nicht tut. Dazu kommt endlich noch, daß sein Wohlklang außerordentlich wenig getrübt ist, so daß er der mildeste aller dissonanten Akkorde ist. Wir sind deshalb in der neueren Musik kaum noch im Stande ihn zu entbehren. Erfunden ist er im Anfange des 17. Jahrhunderts durch Monteverde, wie es scheint.

2. Der Septimenakkord auf der Secunde der Durtonart, d — f — a — c, enthält drei Töne, welche dem Klange F angehören, nämlich f, a und c. D ist bei genauer Intonation dissonant zu allen drei Tönen des Akkordes, und als die dissonante Note desselben zu betrachten. Die fundamentale Lage dieses Akkordes ist also die, welche schon Rameau als solche aufgefaßt hat, und worin F als Grundton erscheint: f — a — c' — d', also die Quintsextenlage, oder wie Rameau sie nennt, der Akkord der großen Sexte. In dieser Lage pflegt der Akkord auch in der Kadenz der C-Durtonart zu erscheinen. Seine Deutung und Beziehung zur Tonart ist wiederum sicherer, als die des früher besprochenen falschen Mollakkordes d — f — a, welcher in der Ausführung durch den Sänger und bei ungenauer Stimmung der Verwechselung mit d — f — a aus der A-Molltonart unterworfen ist. Wir gelangen in einen konsonanten Akkord, wenn wir d — f — a in d — f — a verwandeln. Die Neigung dazu wird sehr groß sein, sobald in der melodischen Fortschreitung die Verwandtschaft des d zum G nicht sehr stark hervorgehoben ist. Wollten wir aber auch in dem Akkorde d — f — a — c das d in d verwandeln, so würden wir es dadurch zwar gegen f und a konsonant machen, aber nicht gegen c. Im Gegenteile ist die Dissonanz d — c schärfer als d — c, und es würde immer nur der Ton a in den Klang des d eintreten, so daß trotz dieser Änderung f, welches drei Töne des Akkordes in seinen Klang vereinigt, das Übergewicht als Grundton behalten würde über d, welches nur zwei vereinigt. Ich finde dem entsprechend, daß auf dem natürlich gestimmten Harmonium der Akkord f — a — c — d, als Subdominantenakkord von C-Dur, eine bessere Wirkung macht, als f — a — c — d.

3. Der entsprechende Septimenakkord auf der Secunde der Molltonartd — f —  — c enthält nur den Ton c, welcher als Bestandteil entweder des Klanges f oder des Klanges  betrachtet werden kann. Da aber c der dritte Partialton von f und erst der fünfte von  ist, so hat auch hier in der Regel f das Übergewicht als Grundton, und der Akkord ist zu betrachten als Subdominantenakkord f —  — c mit Zusatz des dissonanten Tones d. Zur Veränderung des d in d ist hier noch weniger Veranlassung als in dem entsprechenden Durakkorde,

4. Der Septimenakkord auf der Septime der Durtonart h — d — f — a enthält zwei Töne h und d, welche dem Klange der Dominante G angehören, und zwei, nämlich f und a, welche in den Klang F gehören. Der Akkord zerfällt also in zwei gleich gewichtige Hälften. Indessen ist zu bemerken, daß die beiden Töne f und a den beiden nächsten Partialtönen des G-Klanges außerordentlich nahe kommen. Die Töne des G- Klanges vom vierten ab können nämlich geschrieben werden:

Vorausgesetzt, daß man die Ordnung der Töne möglichst bewahrt, namentlich a als höchsten Ton erhalt, wird der Akkord immer noch als G-Klang wiedererkannt werden können, und diesen vertreten.

Hierin scheint mir einfach der Grund zu liegen, warum die Musiker es wünschenswert finden, daß a des Akkordes h — d — f — a den obersten Ton bilden zu lassen. Hauptmann stellt dies sogar unbedingt als Regel auf, indem er eine ziemlich künstliche Begründung dieser Regel gibt. Es wird dadurch die Zweiheit dieses Akkordes, so weit es möglich ist, aufgehoben, und er bekommt eine deutlich verständliche Beziehung zur Dominante der C-Durtonart, während bei anderen Lagen desselben Akkordes die Verwechselung mit dem Subdominantenakkord von A-Moll nahe liegen wird. Übrigens klingt nun auch bei reiner Stimmung der aus den Partialtönen des G-Klanges zusammengestellte Akkord g — h — d — f' — a' sehr weich und wenig dissonant. Der Nonenakkord der G-Durtonart g — h — d' — f' — a' und der Septimenakkord in der Lage h — d' — f' — a' klingen etwas rauher, wegen der Pythagoräischen Terz d' — f' und der unreinen Quinte d' — a', aber sie sind nicht sehr scharf. Dagegen werden sie sehr rauh, wenn man das a' tiefer legt.

Der Septimenakkord h — d — f — a mit dem darauf folgenden Dreiklange c — e — g enthält, wie schon vorher bemerkt ist, sämtliche Töne der C-Durtonleiter, so daß diese Akkordverbindung die Tonart sehr kurz und vollständig feststellt.

5. Der verminderte Septimenakkord h — d — f —  teilt die letztere Eigenschaft mit dem entsprechenden Akkorde der Durtonart, er wird deshalb und wegen seiner großen Veränderlichkeit in der neueren Musik außerordentlich viel, vielleicht übermäßig viel zu Modulationen benutzt. Er enthält keinen Ton, der zu dem Klange irgend einer anderen Note des Akkordes gehörte, wohl aber kann man die drei Töne h — d — f als dem Klange der Dominante G angehörig betrachten, daher er auch als Nonenakkord in der Zusammensetzung

                                                        g — h — d — f — 

6. Die Septimenakkorde mit großer Septime im unverwendeten Akkordsysteme der Tonart f — a — c — e und c — e — g — h in C-Dur,  — c — — g in C-Moll repräsentieren, wie schon früher bemerkt wurde, hauptsächlich einen Durakkord mit der großen Septime als dissonantem Tone. Die große Septime bildet eine ziemlich harte Dissonanz, und steht in sehr entschiedenem Widerspruche mit dem unterliegenden Klange, in welchen sie ganz entschieden nicht hineinpaßt.

7. Die Septimenakkorde mit kleiner Septime im unverwendeten Systeme, a — c — e — g und e — g — h — d, lassen allerdings den Klang ihrer Terz am meisten hervortreten, dem ihr Grundton als beigefügt erscheint, c — e — g — a ist der C-Klang mit zugefügtem a, g — h — d — e der G-Klang mit zugefügtem e. Da aber c — e — g und g — h — d die oft wiederkehrenden Hauptakkorde der Tonart sind, so macht die Anfügung des a oder e in jenen Septimenakkorden durch den Kontrast einen verhältnismäßig stark hervortretenden Eindruck; außerdem sind die Grundtöne jener Septimenakkorde nicht so isoliert, wie der des Akkordes d — f — a — c, welcher keine reine Quinte im Akkorde hat. Das a in a — c — e — g hat die Quinte e und allenfalls auch die Septime g, die seinem Klange angehören; ebenso kann man in e, — g — h — d das h und d dem Klange e zurechnen. Daher sind die Töne a, im ersten und e im zweiten auch nicht notwendig den Stimmführungsgesetzen der Dissonanzen unterworfen.

Die Harmoniker pflegen als normale Lage aller dieser Akkorde immer die des Septimenakkordes zu betrachten, und dessen Grundton als Hauptton des Akkordes. Vielleicht wäre es natürlicher, c — e — g — a als Hauptlage des Akkordes a — c — e — g zu betrachten, und C als Fundamentalton. Letzterer Akkord ist aber ein C-Klang mit Hinneigung zum a, und in den Modulationen wird gerade diese Einmischung des a-Klanges benutzt, um nach den Verwandten von a, die nicht mit dem Akkorde c — e — g verwandt sind, hinzuschreiten, nämlich nach d — f — a. Ebenso kann man von g — h, — d — e nach a — c — e schreiten, was von g — h — d aus immer ein Sprung wäre. Für die Modulation sind also allerdings a und e wesentliche Bestandteile des Akkordes, und in dieser praktischen Rücksicht kann man ihnen auch wohl den Namen der Fundamentaltöne der betreffenden Akkorde lassen.

8. Der Septimenakkord auf der Tonica der Molltonart c —  — g — h wird selten gebraucht, weil das h wesentlich der aufwärtsschreitenden Bewegung in der Molltonart angehört, die regelmäßig sich auflösende Septime aber sinken muß. So würde es immer besser sein, den Akkord c —  — g —  zu bilden, der dann den unter 7. genannten Akkorden ähnlich ist.