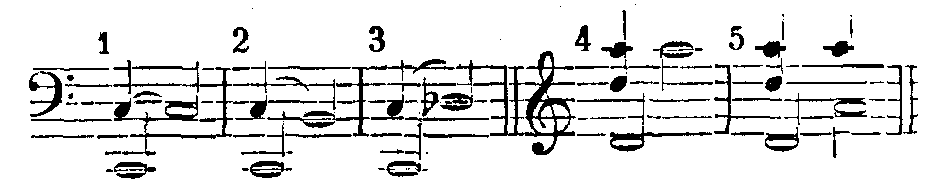
Schwebungen der Obertöne.
Wir haben bisher nur solche Schwebungen betrachtet, welche von je zwei einfachen Tönen hervorgerufen werden, ohne daß sich Obertöne oder Kombinationstöne einmischen. Es konnten dergleichen Schwebungen nur entstehen, wenn die beiden angegebenen Töne um ein verhältnismäßig kleines Intervall von einander entfernt sind. Wenn ihre Entfernung auch nur zur Größe einer kleinen Terz anwächst, werden ihre Schwebungen undeutlich. Nun ist es aber bekannt, daß Schwebungen auch entstehen können durch je zwei Töne, welche um viel größere Intervalle von einander abstehen, und wir werden später sehen, daß diese Schwebungen eine Hauptrolle bei der Feststellung der konsonanten Intervalle unserer musikalischen Tonleiter spielen; daher wir hier auf ihre Untersuchung näher eingehen müssen. Dergleichen Schwebungen von solchen Klängen, die in der Tonleiter weiter als eine kleine Terz von einander entfernt sind, kommen zu Stande durch den Einfluß der Obertöne und der Kombinationstöne. Wenn die Klänge mit deutlich hörbaren Obertönen versehen sind, sind die Schwebungen, welche durch diese entstehen, meistens viel stärker und deutlicher als die der Kombinationstöne, auch ist der Grund dieser Schwebungen viel leichter nachzuweisen. Wir beginnen deshalb die Untersuchung der Schwebungen weiterer Intervalle mit den Schwebungen, welche durch Hilfe der Obertöne hervorgebracht werden. Aber allerdings ist zu bemerken, daß Schwebungen der Kombinationstöne viel all gemeiner vorkommen, bei allen Arten von Klängen, Schwebungen der Obertöne dagegen natürlich nur bei Klängen mit deutlich ausgesprochenen Obertönen. Da aber die musikalisch brauchbaren Klänge mit wenigen Ausnahmen reichlich mit kräftigen Obertönen versehen sind, so haben in der Musik die Schwebungen der Obertöne verhältnismäßig eine viel größere praktische Wichtigkeit, als die Schwebungen der schwachen Kombinationstöne.
Wenn zwei mit Obertönen versehene Klänge angegeben werden, so ist es nach dem Bisherigen leicht ersichtlich, daß Schwebungen entstehen können, so oft je zwei Obertöne beider Klänge einander hinreichend nahe liegen, oder auch wenn der Grundton des einen Klanges einem der Obertöne des anderen Klanges sich nähert. Die Zahl der Schwebungen ist natürlich wieder der Differenz der Schwingungszahlen der beiden betreffenden Teiltöne gleich, durch welche die Schwebungen hervorgerufen werden. Ist die Differenz der Schwingungszahlen klein, sind also die Schwebungen langsam, so sind sie, wie ähnlich langsame Schwebungen primärer Töne, verhältnismäßig am deutlichsten zu hören, zu zählen, und überhaupt ihrer ganzen Natur nach zu erkennen. Sie sind ferner desto deutlicher, je stärker diejenigen Teiltöne sind, durch welche sie entstehen; und das sind bei den gewöhnlich gebrauchten Klangfarben der musikalischen Instrumente die Teiltöne von niedriger Ordnungszahl, da in der Regel die Intensität der Teiltöne mit wachsender Ordnungszahl abnimmt.
Man beginne also mit Beispielen etwa folgender Art auf einer Orgel im Prinzipal- oder Geigenregister oder auf einem Harmonium:
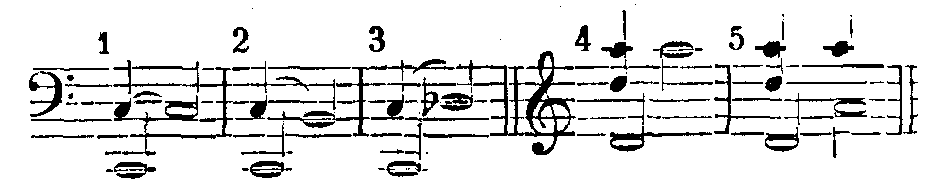
In Beispiel 4 und 5 wird man bei der gewöhnlichen temperierten Stimmung der Tastaturinstrumente Schwebungen hören, und zwar bei genauer Stimmung eine in der Sekunde, weil die Note a'' welche das Instrument angibt, nicht genau übereinstimmt mit dem. a", welches dritter Partialton des Klanges d' ist. Dagegen ist die Note a" des Instruments genau übereinstimmend mit dem a", welches zweiter Partialton der Note a' im fünften Beispiele ist, daher wir im Beispiele 4 und 5 auf einem gut gestimmten Instrumente gleich viel Schwebungen erhalten müssen.
Da der erste Oberton doppelt so viel Schwingungen macht als sein Grundton, so ist im ersten Beispiele das direkt angegebene c mit dem ersten Oberton des tieferen C identisch, wenn das c genau doppelt so viel Schwingungen macht als das C. Nur bei diesem Verhältnisse der Schwingungszahlen von l zu 2 können beide Klänge zusammenklingen, ohne Schwebungen zu geben. Die kleinste Abweichung des Intervalls Cc von dem angegebenen Zahlenverhältnis wird sich durch Schwebungen verraten müssen. Im vierten Beispiele werden die Schwebungen nur dann aufhören, wenn wir das a" des Instruments so stimmen, daß es dem dritten Partialtone des Klanges d genau gleich wird, und dies wird nur dann der Fall sein, wenn die Schwingungszahl des a" genau dreimal so groß ist, als die des d'. Im fünften Beispiele werden wir die Schwingungszahl a' genau halb so groß machen müssen als die des a", welches drei mal so viel Schwingungen macht als d', d. h. die Schwingungszahlen von d' und a' werden sich genau wie 2 zu 3 verhalten müssen, wenn keine Schwebungen eintreten sollen. Jede Abweichung der zusammenklingenden Töne von diesem Zahlenverhältnisse wird sich durch Schwebungen zu erkennen geben.
Daß die Schwingungszahlen zweier Klänge, die das Intervall einer Oktave mit einander bilden, im Verhältnisse von l zu 2, die einer Quinte im Verhältnisse 2 zu 3 stehen, haben wir schon oben angeführt. Es waren diese Zahlenverhältnisse längst gefunden, indem man bloß dem Ohre folgte und die angenehmsten Zusammenklänge je zweier Töne suchte. Hier haben wir nun den Grund gefunden warum diese nach den einfachen Zahlenverhältnissen gestimmten Intervalle allein einen ruhigen Zusammenklang geben, während schon ganz geringe Abweichungen von der mathematischen Stimmung sich verraten durch die unruhig auf und ab wogenden Schwebungen. Das d' und a' des letzten Beispiels, zu einer reinen Quinte gestimmt, machen 2931/3 und 440 Schwingungen, ihr gemeinsamer Oberton a" hat 3 x 2931/3 = 2 x 440 = 880 Schwingungen. In der temperierten Stimmung macht das d' nur 2932/3 Schwingungen, sein zweiter Oberton wird 881 und diese außerordentlich kleine Differenz verrät sich dem Ohre durch eine Schwebung in der Sekunde. Den Orgelbauern ist das Faktum, daß unreine Oktaven und unreine Quinten Schwebungen geben, längst bekannt, und es wird von ihnen benutzt, um schnell und sicher die verlangte reine oder temperierte Stimmung herstellen zu können, da es in der Tat kein empfindlicheres Mittel gibt, die Reinheit der Intervalle zu prüfen.
Zwei Klänge also, welche im Verhältnisse einer reinen Oktave, einer reinen Duodecime oder reinen Quinte stehen, ertönen neben einander in ungestörtem, gleichmäßigem Abflusse, und unterscheiden sich dadurch von ihren nächst benachbarten Intervallen, den unreinen Oktaven oder Quinten, bei denen ein Teil der Klangmaße in einzelne Stöße zerfällt, so daß die beiden Klänge nicht angestört neben einander hinfließen können. Deshalb nennen wir die reine Oktave, Duodecime und Quinte konsonante Intervalle im Gegensatz zu den ihnen nächst benachbarten Intervallen, welche wir dissonant nennen. Obgleich diese Namen längst gegeben waren, ehe man von den Obertönen und ihren Schwebungen etwas wußte, bezeichnen sie doch das Wesen der Sache, ungestörtes oder gestörtes Zusammenklingen, ganz richtig.
Da die hier beschriebenen Erscheinungen die wesentliche Grundlage für die Feststellung der normalen musikalischen Intervalle bilden, so wollen wir sie nach allen Richtungen hin experimentell fest begründen.
Zunächst habe ich behauptet, die Schwebungen seien Schwebungen derjenigen Partialtöne beider Klänge, welche nahehin zusammentreffen. Nun ist es nicht immer ganz leicht, wenn man eine schwach verstimmte Quinte oder Oktave hört, mit unbewaffnetem Ohre deutlich zu erkennen, welche Teile des Gesamtklanges in Schwebung begriffen sind. Es macht leicht den Eindruck, als höre man Verstärkungen und Schwächungen der ganzen Klangmaße. Indessen wird ein Ohr, welches geübt ist die Obertöne zu unterscheiden, wenn es seine Aufmerksamkeit auf den betreffenden gemeinsamen Oberton fixiert, doch leicht die starken Schwebungen gerade dieses Tones hören, während die Grundtöne kontinuierlich fortklingen. Man gebe die Note d' an, richte die Aufmerksamkeit auf ihren Oberton a", lasse die temperierte Quinte a' hinzukommen, so wird man deutlich die Schwebungen des a" hören können. Für ein ungeübtes Ohr sind in diesem Falle die früher beschriebenen Resonatoren von großem Nutzen. Setzt man den Resonator für a" an das Ohr, so hört man die Schwebungen dieses Tones sehr einschneidend. Nimmt man dagegen einen Resonator für einen der Grundtöne d' oder a', so hört man die Schwebungen im Gegenteile schwächer, weil dadurch der kontinuierliche Teil des Tones verstärkt wird.
Diese Behauptung soll natürlich nicht so weit gehen, daß gar keine anderen Töne als das a" des letzten Beispiels Schwebungen gäben. Im Gegenteile, es gibt noch höhere schwächere Obertöne, welche Schwebungen geben, und außerdem werden wir im nächsten Abschnitte die Schwebungen der Kombinationstöne kennen lernen, welche sich zu den hier beschriebenen Schwebungen der Obertöne gesellen. Die Schwebungen des tiefsten gemeinsamen Obertones spielen nur gewöhnlich die Hauptrolle, weil sie von allen die stärksten und die langsamsten sind.
Zweitens mag ein direkter experimenteller Beweis wünschenswert erscheinen, daß die von uns aus den Schwingungszahlen der Obertöne hergeleiteten Zahlenverhältnisse wirklich diejenigen sind, welche keine Schwebungen geben. Dieser Beweis kann am leichtesten durch die oben beschriebene Doppelsirene, Fig. 56, gegeben werden. Man setze die Scheiben in Rotation und öffne an der unteren Scheibe die Reihe von 8, an der oberen von 16 Löchern, so erhält man beim Anblasen zwei Klänge, welche mit einander das Intervall einer Oktave bilden. Sie klingen zusammen ohne Schwebungen, so lange der obere Kasten nicht gedreht wird. So wie man aber anfängt den oberen Kasten langsam umzudrehen, wodurch der Ton der oberen Scheibe etwas erhöht oder erniedrigt wird, hört man Schwebungen. So lange der obere Windkasten stillsteht, ist das Verhältnis der Schwingungszahlen genau l:2, weil bei jeder Umdrehung der Scheibe der untere Kasten genau 8, der obere genau 16 Luftstöße gibt. Durch eine langsame Drehung der Kurbel kann man dieses Verhältnis um so wenig, als man will, verändern, aber bei jeder noch so langsamen Drehung hört man die Schwebungen, welche die Verstimmung des Intervalls ankündigen.
Ähnlich ist es mit der Quinte. Man öffne oben die Reihe mit 12, unten mit 18 Löchern, man wird eine ganz ruhig fortklingende Quinte hören, so lange der obere Windkasten nicht gedreht wird. Das Verhältnis der Schwingungszahlen, gegeben durch die Zahlen der Löcher beider Reihen, ist genau 2 zu 3. So wie man den Windkasten dreht, hört man Schwebungen. Wir haben oben gesehen, daß je eine Umdrehung der Kurbel die Anzahl der Schwingungen des Tones von 12 Löchern um 4 vergrößert oder verkleinert. Wenn wir an der unteren Scheibe ebenfalls den Ton von 12 Löchern erzeugten, erhielten wir 4 Schwebungen. Bei der Quinte von 12 und 18 Löchern erhalten wir dagegen bei jeder Umdrehung der Kurbel 12 Schwebungen, weil die Schwingungszahl des 3ten Partialtones für je eine Umdrehung der Kurbel um 3 x 4 = 12 wächst, wenn die des Grundtones um 4 wächst, und wir es hier mit Schwebungen des genannten Partialtones zu tun haben. Die Sirene hat bei diesen Untersuchungen den großen Vorzug vor allen anderen musikalischen Instrumenten, daß die Stimmung der Intervalle nach den einfachen Zahlenverhältnissen durch ihren Mechanismus selbst in unveränderlicher und fester Weise hergestellt ist, und daß wir deshalb der außerordentlich mühsamen und schwierigen Messungen der Schwingungszahlen überhoben sind, welche dem Beweise unseres Gesetzes vorhergehen müßten, wenn wir andere tönende Instrumente gebrauchen wollten. Das Gesetz war übrigens schon früher durch dergleichen Messungen festgestellt worden, und es hatte sich eine desto genauere Übereinstimmung mit den einfachen Zahlenverhältnissen herausgestellt, je mehr die Methoden, Schwingungszahlen zu messen und rein zu stimmen, vervollkommnet waren.
Wie uns die Koinzidenzen der ersten beiden Obertöne zu den natürlich
bestimmten Konsonanzen der Oktave und Quinte geführt haben, können
wir eine weitere Reihe natürlich bestimmter konsonanter Intervalle
auffinden, indem wir Koinzidenzen der höheren Obertöne hervorbringen.
Nur ist zu bemerken, daß in dem Maße, als diese höheren
Obertöne schwächer werden, auch die Schwebungen weniger vernehmlich
sind, wodurch die verstimmten Intervalle von den rein gestimmten sich unterscheiden.
Die Abgrenzung dieser Intervalle, welche auf Koinzidenzen höherer
Obertöne beruhen; wird deshalb für das Ohr immer schwächer
und unbestimmter, je höhere Obertöne dazu beitragen. In der folgenden
Tabelle enthält die erste Horizontalreihe und die erste Vertikalreihe
die Ordnungszahlen der koinzidierenden Partialtöne, und wo die entsprechende
vertikale und horizontale Reihe zusammentreffen, ist die Benennung und
das Schwingungsverhältnis des entsprechenden Intervalls der Grundtöne
angegeben. Das letztere Zahlenverhältnis ist immer unmittelbar gegeben
durch die Ordnungszahlen der beiden koinzidierenden Partialtöne.
| Koinzidierende Partialtöne. | 1 | 2 | 3 | 4 | 6 |
|
|
|
l:3 |
l:2 |
2:3 |
Terz 5:6 |
|
|
|
|
|
|
|
|
|
l:4 |
|
3:4 |
|
|
|
|
l:3 |
|
|
|
|
|
|
l:2 |
|
|
|
|
Die beiden untersten Reihen dieser Tafel enthalten die schon besprochenen Intervalle der Oktave, Duodecime und Quinte. In der dritten von unten kommt durch den Ton 4 hinzu das Intervall der Quarte und der Doppeloktave. Durch den Ton 5 bestimmt sich die große Terz teils einfach, teils vermehrt um eine oder zwei Oktaven und die große Sexte. Der sechste Ton bringt noch die Heine Terz hinzu. Ich habe die Tabelle hiermit abgebrochen, weil der siebente Partialton auf denjenigen musikalischen Instrumenten, deren Klangfarbe man innerhalb gewisser Grenzen verändern kann, wie zum Beispiel auf dem Klaviere, fortgeschafft, oder sehr geschwächt ist. Auch der sechste Ton ist dann meistens sehr schwach, während man bis zum 5ten hin die Entstehung der Partialtöne zu begünstigen sucht. Wir werden auf die Intervalle, welche durch die Zahl 7 charakterisiert werden, und auf die kleine Sexte, welche durch die Zahl 8 bestimmt wird, später noch einmal zurückkommen. Die Ordnung der konsonanten Intervalle, anfangend von den entschieden charakterisierten, übergehend zu den durch schwächere Schwebungen höherer Obertöne weniger gut begrenzten, ergibt sich hiernach folgendermaßen:
2. Duodecime ..... 13
3. Quinte ... ...... 23
4. Quarte ............. 34
5. Große Sexte .... 35
6. Große Terz .... 45
7. Kleine Terz .... 56

Oktave Duodecime Quinte Quarte Gr. Sexte Gr. Terz Kl. Terz.
1:2 1:3 2:3 3:4 3:5 4:5 5:6
Wir haben bisher immer nur von solchen Fällen gesprochen, wo das angegebene Intervall sehr wenig abweicht von einem der natürlichen konsonanten Intervalle. Bei einer geringen Differenz sind in der Tat die Schwebungen langsam, daher leicht zu bemerken und leicht zu zählen. Natürlich sind sie auch vorhanden, wenn die Abweichung der koinzidierenden Obertöne größer wird. Aber freilich, indem sie zahlreicher werden, verbirgt sich ihr eigentlicher Charakter unter der überwiegenden Klangmaße der stärkeren Grundtöne noch leichter, als dies bei den schnelleren Schwebungen dissonanter Grundtöne selbst geschieht. Die schnelleren Schwebungen erscheinen dann wieder als eine Rauhigkeit der ganzen Klangmaße, ohne daß das Ohr so leicht erkennt, worin diese Rauhigkeit ihren Grund hat. Doch lassen sich die Versuche so einrichten, daß man durch allmählich wachsende Verstimmung eines harmonischen Intervalls die Schwebungen allmählich schneller und schneller werden läßt, wobei man denn alle Zwischenstufen zwischenzählbaren Schwebungen einerseits und der Rauhigkeit einer Dissonanz andererseits verfolgen und sich überzeugen kann, daß beide nur dem Grade nach verschieden sind.
Wir haben bei den Versuchen mit je zwei einfachen Tönen gesehen, daß teils der Abstand derselben in der Skala, teils ihre Anzahl Einfluß hatte auf die Deutlichkeit und die Rauhigkeit ihrer Schwebungen, in der Weise, daß bei den höheren Tönen namentlich die wachsende Zahl der Schwebungen es war, welche selbst bei verhältnismäßig ziemlich engen Intervallen ihre Deutlichkeit beeinträchtigte und sie in der Empfindung verwischte. Hier, wo wir es mit Schwebungen der Obertöne zu tun haben, welche meist dem höheren Teile der Skala angehören, wenn die Grundtöne m den mittleren liegen, hat daher ebenfalls namentlich die Anzahl der Schwebungen einen überwiegenden Einfluß auf ihre Schärfe.
Das Gesetz, welches bei gegebener Verstimmung die Anzahl der Schwebungen
eines konsonanten Intervalls bestimmt, ergibt sich leicht aus dem oben
angeführten Gesetze für die Schwebungen einfacher Töne.
Wenn zwei einander nahe einfache Töne Schwebungen hervorbringen, ist
die Anzahl der Schwebungen in der Sekunde gleich der Differenz ihrer Schwingungszahlen.
Nehmen wir jetzt als Beispiel an, daß ein Grundton 300 Schwingungen
in der Sekunde mache. Zu diesem bestimmen sich nun die Schwingungszahlen
der harmonischen Intervalle folgendermaßen:
|
|
|
| Höhere Oktave .......... = 600 | Tiefere Oktave .......... = 150 |
| Höhere Quinte ........... = 450 | Tiefere Quinte ........... = 200 |
| Höhere Quarte ........... = 400 | Tiefere Quarte ........... = 225 |
| Höhere große Sexte ... = 500 | Tiefere große Sexte.... = 180 |
| Höhere große Terz ..... = 375 | Tiefere große Terz ..... = 240 |
| Höhere kleine Terz .... = 360 | Tiefere kleine Terz .... = 250 |
Wenn wir nun annehmen, der Grundton 300 sei verstimmt worden um eine Schwingung, so daß er 301 Schwingungen in der Sekunde mache, so ergibt sich die Zahl der Schwebungen, welche bei den verschiedenen konsonanten Intervallen dadurch entsteht, wenn man die Schwingungszahlen der koinzidierenden Obertöne berechnet und deren Differenz nimmt, wie folgt:
|
|
|
Zahl der Schwebungen | |
| Prime ...... | 1.300 = 300 | 1.301 = 301 | l |
| Oktave ...... | 1.600 = 600 | 2.801 = 602 | 2 |
| Quinte ...... | 2.450 = 900 | 3.301 = 903 | 3 |
| Quarte . .. | 3.400 = 1200 | 4.301 = 1204 | 4 |
| Große Sexte ... | 3.500 = 1500 | 5.301 = 1505 | 5 |
| Große Terz ... | 4.375 = 1500 | 5.301 = 1505 | 5 |
| Kleine Terz ... | 5.360 = 1800 | 6.301 = 1806 | 6 |
|
|
|
Zahl der Schwebungen | |
| Prime | 1.300 = 300 | 1.301 = 301 | 1 |
| Oktave ..... | 2.150 = 300 | 1.301 = 301 | l |
| Quinte ...... | 3.200 = 600 | 2.301 = 602 | 2 |
| Quarte ..... | 4.225 = 900 | 3.301 = 903 | 3 |
| Große Sexte ... | 5.180 = 900 | 3.301 = 903 | 3 |
| Große Terz ... | 5.240 = 1200 | 4.301 = 1204 | 4 |
| Kleine Terz ... | 6.250 = 1500 | 5.301 = 1505 | 5 |
Die Anzahl der Schwebungen, welche bei der Verstimmung eines Tones in einer der angeführten Konsonanzen um eine Schwingung in der Sekunde entsteht, wird also immer gegeben durch die beiden Zahlen, welche das Intervall charakterisieren, und zwar gibt die kleinere Zahl die Zahl der Schwebungen an, welche entstehen, wenn der höhere Ton eine Schwingung mehr macht, die größere Zahl dagegen, gehört der Verstimmung des tieferen Tones an. Diese Regel ist allgemein gültig. Nehmen wir also die Sexte c a, deren Zahlenverhältnis 3:5 ist, und lassen a in einer bestimmten Zeit eine Schwingung mehr ausführen, so bekommen wir für dieselbe Zeit drei Schwebungen des Zusammenklanges, und lassen wir c in der gleichen Zeit eine Schwingung mehr machen, so erhalten wir fünf Schwebungen u. s. w.
Unsere Berechnung und die darauf gegründete Regel ergeben nun,
daß bei gleicher Verstimmung eines Tones die Zahl der Schwebungen
der konsonanten Intervalle in dem Maße steigt, als diese Intervalle
durch größere Zahlen ausgedrückt werden. Bei den Sexten
und Terzen muß man deshalb dem normalen Schwingungsverhältnis
sich viel genauer anschließen, wenn man langsame Schwebungen vermeiden
will, als bei den Oktaven und den Einklängen. Andererseits aber kommt
man auch bei geringer Verstimmung der Terzen viel eher an die Grenze, wo
die Schwebungen wegen zu großer Anzahl sich zu verwischen beginnen
und ihre Deutlichkeit verlieren. Wenn ich den Einklang c" c"
durch Verstimmung des einen Tones verändere in den Halbton h'
c", so erhalte ich beim Zusammenklang die scharfe Dissonanz von
33 Schwebungen, welche Anzahl, wie ich früher angeführt habe,
etwa das Maximum der Rauhigkeit gibt. Will ich die Quinte f' c" auf
33 Schwebungen verstimmen, so darf ich das c" nur um 1/4
Ton verändern. Verändere ich es um 1/2
Ton, so daß f' c' zu f' h' wird, so erhalte ich
66 Schwebungen, deren Schärfe schon beträchtlich verwischt ist.
In der Quinte c" g" darf ich das c" sogar nur um
1/6 Tonstufe ändern, wenn ich 33 Schwebungen
behalten will, in der Quarte c" f'' um 1/8,
in der großen Terz c"e" und in der Sexte c"a" um
1/10, und in der kleinen Terz c" es" um 1/12
Tonstufe. Umgekehrt, wenn ich in jedem dieser Intervalle das c"
um 33 Schwingungen verändere, so daß es h' oder des"
wird, so erhalte ich folgende Schwingungszahlen:
| Das Intervall der | geht über in | oder in | und gibt Schwebungen |
| Oktave ..................... c" - c'" | h' - c'" | des" - c'" | 66 |
| Quinte .................... c" - g" | h' - g" | des" - g" | 99 |
| Quarte ................... c" - f" | h' - f" | des" - f" | 132 |
| Großen Terz.......... c" - e" | h' - e" | des" - e" | 165 |
| Kleinen Terz.......... c" - es" | h ' - es" | des" - es" | 198 |
Wenn nun 99 Schwebungen schon unter günstigsten Umständen bei einfachen Tönen sehr schwach wirken, 132 an der Grenze des Wahrnehmbaren zu liegen scheinen, so dürfen wir uns nicht wandern, wenn solche Zahlen von Schwebungen, hervorgebracht durch schwächere Obertöne und überdeckt von den stärkeren Grundtönen, keinen merklichen Eindruck mehr machen und dem Ohre verschwinden. Dieses Verhältnis ist aber für die musikalische Praxis von sehr großer Wichtigkeit, denn in unserer letzten Tabelle finden wir als verstimmte Quinte vor das Intervall h'g", welches unter dem Namen der kleinen Sexte als unvollkommene Konsonanz gebraucht wird. Ebenso finden wir als verstimmte Quarte die große Terz des" f", als verstimmte große Terz die Quarte h e" vor u. s. w. Daß wenigstens in dieser Gegend der Tonleiter die große Terz nicht die Schwebungen einer verstimmten Quarte, und die Quarte nicht die Schwebungen einer verstimmten großen Terz hören läßt, erklärt sich aus der großen Zahl der Schwebungen. Es klingen vielmehr die genannten Intervalle in der angegebenen Lage vollkommen gleichmäßig abfließend, ohne eine Spur wahrnehmbarer Schwebungen und Rauhigkeiten, wenn sie rein gestimmt sind.
Wir kommen hiermit zur Erörterung derjenigen Umstände, welche auf die Vollkommenheit der Konsonanz in den verschiedenen Intervallen Einfluß haben. Wir haben die Konsonanzen dadurch charakterisiert, daß irgend welche zwei Partialtöne beider Klänge zusammenfallen. Wenn dies geschieht, können die beiden Klänge zusammen keine langsamen Schwebungen ausführen. Wohl aber ist es möglich, daß gleichzeitig irgend welche andere zwei Obertöne beider Klänge einander so nahe kommen, daß sie schnelle Schwellungen mit einander hervorbringen. Fälle dieser Art haben sich schon in den letzten Notenbeispielen gezeigt. Unter den Obertönen der großen Terz FA kommen nebeneinander f' und e' vor, unter denen der kleinen Terz F As die Töne a' und as', welche mit einander die Dissonanz eines halben Tones bilden, und dieselben Schwebungen hervorrufen müssen, wie wenn die betreffenden Obertöne direkt als einfache Grundtöne angegeben würden. Obgleich nun solche Schwebungen teils wegen ihrer Anzahl, teils wegen der Schwäche der sie hervorbringenden Töne, teils wegen des gleichzeitigen Erklingens der gleichmäßig daneben hertönenden Grundtöne und übrigen Partialtöne keinen sehr hervortretenden Eindruck machen können, so werden sie doch nicht ganz ohne Einfluß auf den Wohlklang des Intervalls sein. Der vorige Abschnitt hat uns gezeigt, daß in gewissen Klangfarben, wo die hohen Obertöne sehr entwickelt sind, selbst innerhalb eines einzigen Klanges Dissonanzen entstehen können, deren Rauhigkeit dem Ohre fühlbar wird. Sobald je zwei Klänge solcher Art zusammenkommen, werden zu den dissonanten Intervallen zwischen den Obertönen jedes einzelnen Klanges auch noch solche hinzukommen können zwischen je einem Obertone des einen und einem Obertone des zweiten Klanges, wodurch notwendig eine gewisse Vermehrung der Rauhigkeit entstehen muß.
Eine Methode, um für jedes konsonante Intervall diejenigen Obertöne leicht aufzufinden, welche Dissonanzen mit einander bilden, ergibt sich aus dem, was wir über stärkere Verstimmung der konsonanten Intervalle schon beigebracht haben. Wir haben dort die Terz als eine verstimmte Quarte, die Quarte als eine verstimmte Terz auftreten sehen. Wenn wir die Höhe eines Klanges um einen halben Ton verändern, verändern wir auch die Höhe aller seiner Obertöne um einen halben Ton. Diejenigen Obertöne, welche in dem Quartenintervall zusammenfallen, treten um einen Halbton auseinander, wenn wir die Quarte um einen halben Ton verändern, so daß sie große Terz wird, und umgekehrt, diejenigen, welche in der Terz zusammenfallen, müssen um einen Halbton auseinander treten in der Quarte, wie folgendes Beispiel zeigt:
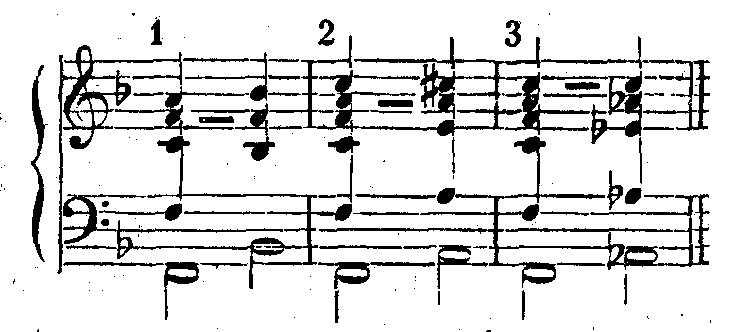
In jedem konsonanten Intervalle dissonieren also diejenigen Obertöne, welche in den benachbarten Intervallen zusammenfallen, und man kann in diesem Sinne sagen, daß jede Konsonanz durch die Nähe der in der Tonleiter benachbarten Konsonanzen gestört wird, und zwar um so mehr gestört wird, je niedriger und stärker die Obertöne sind, welche das störende Intervall durch ihre Koinzidenz charakterisieren, oder was dasselbe sagt, je kleinere Zahlen das Schwingungsverhältnis desselben ausdrücken.
Folgende Tabelle gibt nun eine Übersicht dieses Einflusses der
verschiedenen Konsonanzen auf einander. Es sind die Obertöne bis zum
neunten aufgenommen und den durch Koinzidenz der höheren Obertöne
entstehenden Intervallen entsprechende Namen beigelegt worden. Die dritte
Columne enthält das Verhältnis ihrer Schwingungszahlen, welches
zugleich die Ordnungszahlen der koinzidierenden Partialtöne angibt.
Die vierte Columne gibt den Abstand der einzelnen Intervalle von einander
an, und die letzte gibt ein Maß für die relative Stärke
der Schwebungen, welche durch Verstimmung des betreffenden Intervalls entstehen,
berechnet für die Klangfarbe der Violine1). Je größer
die hierin enthaltene Zahl ist, desto mehr stört das betreffende Intervall
die benachbarten.
| Intervalle | Notation | Verhältnis der Schwingungszahlen | Gegenseitiger Abstand | Stärke des Einflusses |
| Prime |
|
1:l | 8:9
63:64 48:49 35:36 24:25 35:36 27:28 20:21 14:15 15:16 24:25 20:21 35:36 9:10 |
100 |
| Sekunde ....... | D | 8:9 | 1,4 | |
| Übermäßige Sekunde . | D+ | 7:8 | 1,8 | |
| Verminderte Terz . . . | Es | 6:7 | 2, 4 | |
| Kleine Terz ...... | Es | 5:6 | 3,3 | |
| Große Terz ...... | E | 4:5 | 5,0 | |
| Übermäßige Terz . . | E+ | 7:9 | 1,6 | |
| Quarte ........ | F | 3:4 | 8,3 | |
| Verminderte Quinte . . | Ges | 5:7 | 2,8 | |
| Quinte ........ | G | 2:3 | 16,7 | |
| Kleine Sexte ..... | As | 5:8 | 2,5 | |
| Große Sexte ..... | A | 3:5 | 6,7 | |
| Verminderte Septime . | B | 4:7 | 3,6 | |
| Kleine Septime .... | B | 6:9 | 2,2 | |
| Oktave ........ | C | 1:2 | 50 |
Ähnlich verhält es sich mit der Oktave. Sämtliche Partialtöne der höheren Note dieses Intervalls fallen mit den geradzahligen Partialtönen der tieferen Note zusammen und verstärken diese, so daß auch in diesem Falle keine Dissonanz der Obertöne entstehen kann, die nicht, wenn auch schwächer, schon in dem tieferen Klange an sich enthalten wäre. Ein Klang, der von seiner Oktave begleitet wird, erhält dadurch eine etwas schärfere Klangfarbe, indem die hohen Partialtöne, welche die Schärfe der Klangfarbe bedingen, durch die hinzugesetzte Oktave zum Teil verstärkt werden, diese Wirkung würde aber in ähnlicher Weise eintreten, wenn man den Grundton des Intervalls einfach an Stärke wachsen ließe, ohne die Oktave hinzuzufügen; nur würde in diesem Falle die Verstärkung auf die verschiedenen Obertöne sich etwas anders verteilen.
Dasselbe gilt von der Duodecime und zweiten Oktave, überhaupt von allen den Fällen, wo der höhere Klang mit einem Oberton des tieferen zusammenfällt, nur daß bei zunehmender Entfernung beider Klänge der Unterschied zwischen Konsonanz und Dissonanz sich immer mehr verwischt.
Die bisher betrachteten Fälle, wo der höhere Klang mit einem der Partialtöne des tieferen zusammenfällt, können wir absolute Konsonanzen nennen. Der zweite Klang bringt hier nichts Neues hinzu, er verstärkt nur einen Teil des ersten Klanges.
Prime und Oktave stören nun die ihnen zunächst liegenden Intervalle beträchtlich, so daß die kleine Sekunde CDes und die große Septime C H, welche um einen Halbton beziehlich von der Prime und Oktave abstehen, die schärfsten Dissonanzen unserer Tonleiter sind. Auch die große Sekunde CD und die kleine Septime C B, bei denen die Entfernung von den störenden Intervallen einen ganzen Ton beträgt, muß man zu den Dissonanzen rechnen, doch sind sie wegen des größeren Abstandes der dissonierenden Töne viel milder, als die erstgenannten. Namentlich in den h oberen Gegenden der Tonleiter nimmt ihre Rauhigkeit sehr ab, wegen der großen Zahl ihrer Schwebungen. Da die kleine Septime ihre Dissonanz dem ersten Obertone verdankt, welcher in den meisten musikalischen Klangfarben schwächer ist als der Grundton, so ist ihre Dissonanz noch milder als die der großen Sekunde, und sie steht an der Grenze der Dissonanzen.
Neue gute Konsonanzen müssen wir also in der Mitte des Oktavenintervalls suchen, und hier ist es zunächst die Quinte, welche uns begegnet. Unmittelbar neben sich in der Entfernung eines Halbtones hat sie in unserer letzten Tabelle nur die Intervalle 5:7 und 5:8, welche wenig oder gar nicht stören können, weil bei den besseren musikalischen Klangfarben der siebente und achte Ton sehr schwach ausfallen oder ganz fehlen. Die nächsten Intervalle mit stärkeren Obertönen sind die Quarte 3:4 und die große Sexte 3:5. Indessen hier ist der Abstand ein ganzer Ton, und wenn bei dieser Entfernung schon die Töne l und 2 des Oktavenintervalls nur wenig stören in der kleinen Septime, so ist natürlich die Störung durch die Töne 2 und 3 oder durch die Nachbarschaft der Quinte für die Quarte und große Sexte unbedeutend, und ganz zu vernachlässigen ist die Rückwirkung beider Intervalle mit den Tönen 3 und 4 oder 3 und 5 auf die Quinte. So bleibt die Quinte eine vollkommene Konsonanz, in welcher so gut wie gar keine Störung durch Dissonanzen eng zusammenliegender Obertöne merklich wird; nur bei scharfen Klangfarben (Harmonium, Contrabaß, Violoncell, Zungenregister der Orgel) mit hohen Obertönen und in sehr tiefer Lage, wenn die Zahl der Schwebungen gering ist, bemerkt man, daß die Quinte etwas rauher klingt, als die Oktave. Daher ist die Quinte auch seit ältester Zeit und bei allen Musikern als Konsonanz anerkannt worden. Dagegen sind die der Quinte zunächst benachbarten Intervalle diejenigen, welche nächst den der Oktave benachbarten die schärfsten Dissonanzen bilden, und zwar die zwischen Quinte und Quarte liegenden, die von der einen Seite durch die Töne 2 und 3, von der anderen durch die Töne 3 und 4 gestört werden, noch entschiedener als diejenigen, welche zwischen Quinte und großer Sexte liegen, weil bei den letzteren statt der Störung durch den Ton 4 die durch den schwächeren Ton 5 eintritt. Die zwischen Quinte und Quarte liegenden Intervalle werden deshalb in der musikalischen Praxis stets als Dissonanzen betrachtet; zwischen Quinte und großer Sexte liegt dagegen das Intervall der kleinen Sexte, welches als unvollkommene Konsonanz behandelt wird, und diesen Vorzug weniger seinem Wohlklange verdankt, als dem Umstande, daß es die Umkehrung der großen Terz ist, wie denn auch auf den Tastaturinstrumenten je nach der Tonart derselbe Anschlag bald die Konsonanz GAs bald die Dissonanz C Gis repräsentieren muß.
Auf die Quinte folgen zunächst die Konsonanzen der Quarte 3:4 und großen Sexte 3:5, deren Hauptstörung von der Quinte auszugeben pflegt. Die Quarte liegt der Quinte etwas ferner (Abstand gleich dem Intervall 8:9) als die Sexte (Abstand 9:10), daher letztere eine unvollkommenere Konsonanz als die Quarte ist. Doch hat diese die große Terz mit den koinzidierenden Obertönen 4 und 5 dicht neben sich, und wenn die Obertöne 4 und 5 stark entwickelt sind, kann deshalb jener Vorteil der Quarte wieder aufgehoben werden. Auch ist bekannt, daß ein langer Streit über die Natur der Quarte, ob sie Konsonanz oder Dissonanz sei, von den älteren theoretischen Musikern geführt worden ist. Die bevorzugte Stellung, welche der Quarte neben der großen Sexte und großen Terz gegeben wird, verdankt sie mehr dem Umstände, daß sie die Umkehrung der Quinte ist, als ihrem hervorstechenden Wohlklange. Die Quarte sowohl wie die große und kleine Sexte verschlechtern sich, wenn sie um eine Oktave erweitert werden, weil sie dann in die Nähe der Duodecime zu liegen kommen und daher sowohl die Störung durch die charakteristischen Töne der Duodecime l und 3 stärker wird, als durch die nebenliegenden Intervalle 2:5 und 2:7, welche mehr stören als 4:5 und 4:7 in der unteren Oktave.
Alsdann folgen in der Reihe der Konsonanzen die große und die kleine Terz. Die letztere ist in solchen Fällen, wo der sechste Ton des Klanges schwach entwickelt ist, wie auf den neueren Pianofortes, nur noch sehr unvollkommen abgegrenzt, da ihre Verstimmung kaum noch deutlich wahrnehmbare Schwebungen hervorruft. Die kleine Terz ist der Störung durch den Grundton noch merklich ausgesetzt, die große Terz der Störung durch die Quarte; beide stören sich außerdem gegenseitig, wobei die kleine Terz schlechter wegkommt als die große. Für den Wohlklang beider Intervalle ist es daher wesentlich, daß die Zahl der Schwebungen, durch welche ihr Wohlklang verunreinigt wird, groß sei. In höheren Teilen der Tonleiter klingen sie vollkommen rein und gut, in niederen dagegen rauh. Das ganze Altertum hat sich daher geweigert, die Terzen als Konsonanzen anzuerkennen, erst seit der Zeit Franco's von Köln (Ende des zwölften Jahrhunderts) begann man sie als unvollkommene Konsonanzen zuzulassen. Der Grund hiervon mag darin zu suchen sein, daß die Theorie der Musik bei den klassischen Völkern und im Mittelalter sich hauptsächlich am Gesange der Männerstimmen entwickelt hat und in so tiefer Lage die Terzen in der Tat nicht besonders gut klingen. Damit hängt es denn wohl zusammen, daß man auch die richtige Stimmung der Terzen nicht fand, und die sogenannte pythagoräische Terz 64:81 bis gegen das Ende des Mittelalters als die normale betrachtet wurde.
Ich habe oben schon hervorgehoben, welchen wichtigen Einfluß auf den Wohlklang der Konsonanzen, namentlich der unvollkommeneren, die Anzahl der schwachen Schwebungen der dissonanten Obertöne hat. Wenn wir die Intervalle alle über denselben Grundton legen, so ist die Zahl ihrer Schwebungen sehr verschieden, bei den unvollkommenen viel größer, als bei den vollkommenen. Wir können aber allen von uns bisher aufgeführten Intervallen eine solche Lage in der Tonleiter geben, daß die Anzahl der Schwebungen gleich groß ist. Da wir für einfache Töne gefunden haben, daß 33 Schwebungen in der Sekunde etwa das Maximum der Rauhigkeit geben, so habe ich in dem hier folgenden Notenbeispiel die Intervalle in der Lage zusammengestellt, wo sie 33 Schwebungen geben. Es ist die Stimmung der reinen C-Dur-Tonleiter vorausgesetzt. Der Ton b soll die verminderte Septime von c (4:7) bedeuten.

Die Töne dieses Beispiels sind alle Obertone des C1 von 33 Schwingungen, also ihre eigenen Schwingungszahlen und die ihrer Obertöne alle gleich der Zahl 33 multipliziert mit ganzen Zahlen; die Differenzen dieser Schwingungszahlen, welche die Zahlen der Schwebungen angeben, müssen daher selbst immer wieder 33, 66 oder ein höheres Multiplum von 33 sein.
In der hier angegebenen niedrigen Lage sind. nun die von dissonanten Obertönen herrührenden Schwebungen so wirksam, als sie ihrer Intensität nach sein können, und hier sind die Sexten, Terzen und selbst die Quarte ziemlich rauh; doch zeigen die große Sexte und große Terz ihre Überlegenheit über die kleine Terz und kleine Sexte darin, daß sie etwas weiter in der Skala herabsteigen und doch noch etwas weicher klingen als jene. Es ist auch eine allgemein bekannte praktische Regel der Musiker, daß sie in tiefer Lage diese engen Intervalle vermeiden, wenn sie weich klingende Akkorde haben wollen, eine Regel, für welche in den bisherigen theoretischen Darstellungen der Akkordlehre die Rechtfertigung fehlte.
Die von mir hingestellte Theorie des Hörens mittels der mitschwingenden elastischen Nervenanhänge würde erlauben, die Intensität der Schwebungen verschiedener Intervalle zu berechnen, wenn die Intensität der Obertöne in der betreffenden Klangfarbe des gebrauchten Instruments gegeben ist und man die Intervalle so legt, daß die Anzahl ihrer Schwebungen die gleiche ist. Doch fällt eine solche Berechnung je nach den verschiedenen Klangfarben sehr verschieden ans, und hat nur Wert für den einzelnen Fall.
Für Intervalle, welche über demselben Grundton aufgebaut sind, kommt nun noch ein neuer Faktor hinzu, nämlich die Zahl der Schwebungen, deren Einfluß auf die Rauhigkeit der Empfindung sich noch nicht direkt durch ein feststehendes Gesetz ausdrücken läßt. Um aber eine übersichtliche graphische Darstellung der hier zusammenwirkenden verwickelten Verhältnisse geben zu können, welche in einem solchen Falle in einem Überblicke mehr lehrt, als die kompliziertesten Beschreibungen, habe ich eine solche Berechnung durchgeführt und danach die Fig. 60 A und B konstruiert. Um sie durchführen zu können, mußte ich allerdings für die Abhängigkeit der Rauhigkeit von der Anzahl der Schwebungen ein einigermaßen willkürliches Gesetz annehmen. Ich wählte dazu die einfachste mathematische Formel, welche ausdrückt, daß die Rauhigkeit verschwindet, wenn die Anzahl der Schwebungen gleich Null ist, daß sie ein Maximum wird für 33 Schwebungen, und dann bei steigender Anzahl derselben wieder abnimmt. Dann habe ich für die Klangfarbe der Violine die Intensität und Rauhigkeit der Schwebungen berechnet, welche die einzelnen Obertöne paarweise zusammengenommen geben, und nach den Resultaten schließlich die Figuren 60 A und B konstruiert. Die Grundlinien c'c" und c"c'" bedeuten das zwischen den gleichnamigen Noten gelegene Stück der musikalischen Skala, aber so genommen, daß die Tonhöhe kontinuierlich darin steigt, nicht stufenweise. Es ist ferner angenommen, daß die den einzelnen Punkten der Skala entsprechenden Klänge zusammenklingen mit dem Tone c', der den konstanten Grundton aller Intervalle bildet. Fig. 60 A zeigt also die Rauhigkeit der Intervalle, welche kleiner sind als eine Oktave, Fig. 60 B die derjenigen, welche weiter als eine, enger als zwei Oktaven sind. Über den horizontalen Grundlinien sind Hügel aufgetragen, mit den Ordnungszahlen je zweier Obertöne bezeichnet. Die Höhe dieser Hügel an jeder Stelle ihrer Breite ist gleich gemacht der Rauhigkeit, welche die durch die Ziffern angegebenen beiden Obertöne hervorbringen, wenn der Klang von entsprechender Tonhöhe zusammen mit dem c' erklingt. Die Rauhigkeiten, welche die verschiedenen Obertöne hervorbringen, sind über einander getürmt. Man sieht, wie die verschiedenen Rauhigkeiten, die von den verschiedenen Obertönen herrühren, über einander greifen, und daß nur wenige schmale Täler übrig bleiben, entsprechend dem Orte der vorzüglichsten Konsonanzen in denen die Rauhigkeit des Zusammenklanges verhältnismäßig klein wird. Die tiefsten Täler gehören in der ersten Oktave c' c" der Oktave c" und Quinte g' an, darauf folgt die Quarte f', die große Sexte a', die große Terz e' in der Ordnung, wie wir schon vorher diese Intervalle gefunden haben. Die kleine Terz es' und kleine Sexte as' zeigen schon höher liegende Talsohlen, entsprechend der größeren Rauhigkeit dieser Intervalle, Ihnen sehr nahe stehen die mit der 7 gebildeten Intervalle 4:7, 5:7, 6:7.
In der zweiten Oktave verbessern sich im Allgemeinen diejenigen Intervalle der ersten Oktave, in deren Zahlenausdruck die kleinere Zahl eine gerade ist; nämlich die Duodecime l:3, die Dezime 2:5, die verminderte Septime 2:7 und die verminderte Terz 3:7 sind reiner als die Quinte 2:3, als die große Terz 4:5 und die Intervalle 4:7 und 6:7. Die anderen Intervalle sind relativ verschlechtert. Die Undecime oder erweiterte Quarte tritt entschieden zurück gegen die Decime, die Tredecime oder erweiterte große Sexte, ebenso gegen die verminderte Septime; noch ungünstiger stellen sich die kleine Terz und kleine Sexte bei ihrer Erweiterung um eine Oktave wegen der verstärkten Störung durch die Nebenintervalle. Diese hier aus der Berechnung sich ergebenden Folgerungen bestätigen sich leicht beim Versuche an rein gestimmten Instrumenten; daß sie auch in der musikalischen Praxis berücksichtigt werden, trotzdem nach der gewöhnlichen musikalischen Theorie die Natur eines Akkordes als unverändert betrachtet wird, wenn man einzelne seiner Töne um ganze Oktaven verlegt, werden wir später bei der Lehre von den Akkorden und ihren Umlagerungen sehen.
Daß besondere Beschaffenheit einzelner Klangfarben die Reihenfolge des Wohlklanges der Intervalle mannigfach verändern kann, ist schon erwähnt worden. Die Klangfarbe der jetzt gebräuchlichen musikalischen Instrumente ist natürlich ausgesucht und verändert worden mit Rücksicht auf ihre Brauchbarkeit zu harmonischen Verbindungen. Die Untersuchung der Klangfarben unserer Hauptinstrumente hat gezeigt, daß wir für eine gute musikalische Klangfarbe es lieben, wenn die Oktave und Duodecime des Grundtones kräftig, der vierte und fünfte Ton mäßig mitklingen, die höheren Obertöne aber schnell an Stärke abnehmen. Eine solche Klangfarbe vorausgesetzt, können wir die Resultate des vorliegenden Abschnittes wie folgt zusammenfassen:
Wenn zwei musikalische Klänge neben einander erklingen, ergeben sich im Allgemeinen Störungen ihres Zusammenklingens durch die Schwebungen, welche ihre Partialtöne mit einander hervorbringen, so daß ein größerer oder kleinerer Teil der Klangmaße in getrennte Tonstöße zerfällt und der Zusammenklang rauh wird. Wir nennen dies Verhältnis Dissonanz.
Es gibt aber gewisse bestimmte Verhältnisse zwischen den Schwingungszahlen, bei denen eine Ausnahme von dieser Regel eintritt. wo entweder gar keine Schwebungen sich bilden, oder diese Schwebungen so schwach in das Ohr fallen, daß sie keine unangenehme Störung des Zusammenklanges veranlassen; wir nennen diese Ausnahmefälle Konsonanzen.
1. Die vollkommensten Konsonanzen sind diejenigen, welche wir absolute Konsonanzen genannt haben, bei denen der Grundton des einen Klanges mit einem Partialtone des anderen Klanges zusammenfällt. Dahin gehören die Oktave, Duodecime, Doppeloktave.
2. Demnächst folgen die Quinte und die Quarte, welche wir vollkommene Konsonanzen nennen können, weil sie in jedem Teile der Tonleiter ohne erhebliche Störung des Wohlklanges gebraucht werden können. Die Quarte ist von beiden die unvollkommenere Konsonanz, sie nähert sich den Konsonanzen der folgenden Gruppe, und erhält ihren Vorzug in der musikalischen Praxis wesentlich nur dadurch, daß sie in der Akkordbildung die Ergänzung der Quinte zur Oktave bildet, worauf wir in einem späteren Abschnitte zurückkommen werden.
3. Die folgende Gruppe wird gebildet von der großen Sexte und großen Terz, welche wir mittlere Konsonanzen nennen können. Den alten Harmonikern galten sie nur als unvollkommene Konsonanzen. Die Störung des Wohlklanges ist in tiefen Lagen schon sehr merklich, in hohen Lagen verschwindet sie, weil die Schwebungen durch ihre große Zahl sich verwischen. Beide sind bei guten musikalischen Klangfarben aber noch selbständig charakterisiert, indem jede kleine Verstimmung derselben deutliche Schwebungen der Obertöne hervorruft, und so sind beide Intervalle von allen benachbarten scharf geschieden.
4. Die unvollkommenen Konsonanzen der kleinen Terz und kleinen Sexte sind meist nicht mehr selbständig bestimmt, weil die sie begrenzenden Obertöne in guten Klangfarben für die Terz oft, für die Sexte gewöhnlich fehlen, und deshalb kleine Verstimmungen dieser Intervalle nicht notwendig Schwebungen hervorbringen. Sie sind noch weniger in tiefen Lagen anwendbar als die vorigen und verdanken ihren Vorzug als Konsonanzen vor manchen anderen Intervallen, die auf der Grenze zwischen Konsonanzen und Dissonanzen stehen, wesentlich dem Umstande, daß sie notwendig sind in der Akkordbildung als Ergänzungen der großen Sexte und Terz zur Oktave oder Quinte. An Wohlklang ist die verminderte Septime 4:7 sehr häufig der kleinen Sexte überlegen, nämlich immer dann, wenn der dritte Partialton des Klanges, verglichen mit dem zweiten, verhältnismäßig stark ist, wobei dann die Quinte auf die um einen halben Ton von ihr entfernten Intervalle stärker störend einwirkt, als die Oktave auf die von ihr um einen ganzen Ton entfernte kleine Septime. Diese verminderte Septime aber mit anderen Konsonanzen zu Akkorden verbunden, bringt lauter schlechtere Intervalle hervor als sie selbst ist, 6:7, 5:7, 7:8 u. s. w., und wird deshalb in der heutigen Musik nicht als Konsonanz gebraucht.
5. Bei der Erweiterung der Intervalle um eine Oktave verbessern sich unter den genannten Intervallen die Quinte und große Terz als Duodecime und große Decime. Schlechter werden Quarte und große Sexte als Undecime und Tredecime, am schlechtesten die kleine Terz und Sexte als kleine Decime und Tredecime, so daß die letztgenannten bei Weitem durch die Intervalle 2:7 und 3:7 an Wohlklang übertroffen werden.
Die hier aufgestellte Reihenfolge der Konsonanzen berücksichtigt nur den Wohlklang jedes einzelnen Intervalls, wenn dasselbe an und für sich ohne Verbindung mit anderen angegeben wird; es sind dabei alle Beziehungen auf Tonart, Tonleiter und Modulationen unberücksichtigt geblieben. Fast alle musikalischen Theoretiker haben dergleichen Reihenfolgen für die Konsonanzen aufgestellt, die auch in ihren Hauptzügen unter einander und mit der von uns aus der Theorie der Schwebungen hergeleiteten gut übereinstimmen. Namentlich wird von allen der Einklang und die Oktave vorangestellt, als die vollkommensten aller Konsonanzen; demnächst folgt die Quinte ebenfalls bei allen, die Quarte bei denjenigen wenigstens, welche die modulatorischen Eigenschaften der Quarte nicht mit hineingezogen und sich auf die Beobachtung des Wohlklanges des isolierten Intervalls beschränkt haben. In der Anordnung der Sexten und Terzen dagegen herrscht große Verschiedenheit, Bei den Griechen und Römern wurden diese Intervalle überhaupt nicht als Konsonanzen anerkannt, vielleicht weil in der ungestrichenen Oktave, wo sich ihre überwiegend für Männerstimmen berechneten Gesänge bewegten, diese Intervalle in der Tat schlecht klingen, vielleicht weil ihr Ohr überhaupt zu empfindlich war, um auch nur die schwache Zunahme der Rauhigkeit zu ertragen, welche zusammengesetzte Klänge geben, wenn sie in Terzen und Sexten zusammenklingen. Noch in gegenwärtiger Zeit, versichert der Erzbischof Chrysanthus von Dyrrhachium, hätten die Neugriechen kein Gefallen an mehrstimmiger Musik, weshalb er es verschmäht, in seinem Buche über Musik überhaupt sich darauf einzulassen, und die, welche ans Neugierde etwa diese Regeln kennen lernen wollten, auf die abendländischen Schriften verweist2). Ähnlich denken auch die Araber nach den Berichten aller Reisenden.
2) ![]()
1832. Zitiert bei Coussemaker, Histoire de l'Harmonie, p. 5.
Diese Regel blieb bestehen auch während der ersten Hälfte des Mittelalters, als man schon anfing die ersten Versuche mit zweistimmigen Sätzen zu machen. Erst gegen das Ende des 12. Jahrhunderts nahm Franco von Köln die Terzen unter die Konsonanzen auf. Er unterscheidet:
1. Vollkommene Konsonanzen: Einklang und Oktave.
2. Mittlere Konsonanzen: Quinte und Quarte.
3. Unvollkommene Konsonanzen: Große und kleine Terz.
4. Unvollkommene Dissonanzen: Große und kleine Sexte.
5. Vollkommene Dissonanzen: Kleine Sekunde, übermäßige
Quarte, große und kleine Septime3). Erst im 13. und 14. Jahrhundert fing man an, auch die Sexten unter die Konsonanzen zu setzen. Philipp de Vitry und Jean de Muris4) führen als vollkommene Konsonanzen auf den Einklang, die Oktave und Quinte, als unvollkommene die Terzen und Sexten. Die Quarte ist gestrichen. Übrigens werden von dem ersteren Schriftsteller die große Terz und die große Sexte, als die vollkommeneren, den kleinen Intervallen gleiches Namens gegenübergestellt. Dieselbe Ordnung findet sich in Dodecachordon des Glareanus 1557, der nur noch die um eine Oktave erweiterten Intervalle hinzufügt. Daß man die Quarte sowohl aus den vollkommenen wie aus den unvollkommenen Konsonanzen strich, hatte wohl seinen Grund in den Regeln über die Stimmführung. Vollkommene Konsonanzen durften nicht in denselben Stimmen auf einander folgen, Dissonanzen ebenso wenig, wohl aber unvollkommene Konsonanzen, wie die Terzen und Sexten. Andererseits aber konnten die vollkommenen Konsonanzen, Oktaven und Quinten in solchen Akkorden, welche Ruhepunkte bilden sollten, namentlich im Schlußakkorde, vorkommen. Da paßte aber die Quarte des Grundtones dieses Akkordes nicht hin, weil sie nicht in dessen Dreiklang liegt. Andererseits ließ man eine Folge von Quarten in zwei Stimmen auch nicht zu; dazu stand die Quarte der Quinte zu nahe. Also teilte die Quarte in Bezug auf die Stimmführung die Eigenschaften der Dissonanzen, und man setzte sie kurzweg unter die Dissonanzen, während es passender gewesen wäre, für sie eine Mittelstufe zwischen den vollkommenen und unvollkommenen Konsonanzen einzuschieben. Denn was den Wohlklang betrifft, kann kein Zweifel sein, daß bei den meisten Klangfarben die Quarte den großen Terzen und Sexten an Wohlklang überlegen ist, jedenfalls aber der kleinen Terz und Sexte. Die um eine Oktave vergrößerte Quarte, die Undecime, klingt aber bei einigermaßen starkem dritten Teilton. ziemlich schlecht.
3) Gerbert, Scriptores ecclesiastici de musica sacra. Saint-Blaise 1784, T. III, p. 11. Coussemaker, Histoire de l' Harmonie. Paris 1852, p. 49.
4) Coussemaker, l. c. p. 66 und 68.
Der Streit über Konsonanz oder Dissonanz der Quarte zieht sich bis in die neueste Zeit hinein. Noch in der 1840 erschienenen Harmonielehre von Dehn wird die Behauptung festgehalten, sie sei als Dissonanz zu behandeln und aufzulösen; aber freilich schiebt Dehn der Streitfrage einen ganz anderen Sinn unter, indem er die Quarte jedes Grundtones innerhalb seiner Tonart und unabhängig von den mitklingenden Intervallen als Dissonanz zu behandeln vorschreibt. Sonst ist es in der neueren Musik ja fortwährend gebräuchlich, die Verdoppelung des Grundtones als Quarte der Dominante mit dieser zusammen auch in den Schlußakkorden vorkommen zu lassen, und sie ist in diesen Akkorden sogar schon längst gebraucht worden, ehe man noch Terzen dort anzuwenden wagte, so daß sie dadurch praktisch längst als eine der besseren Konsonanzen anerkannt ist.