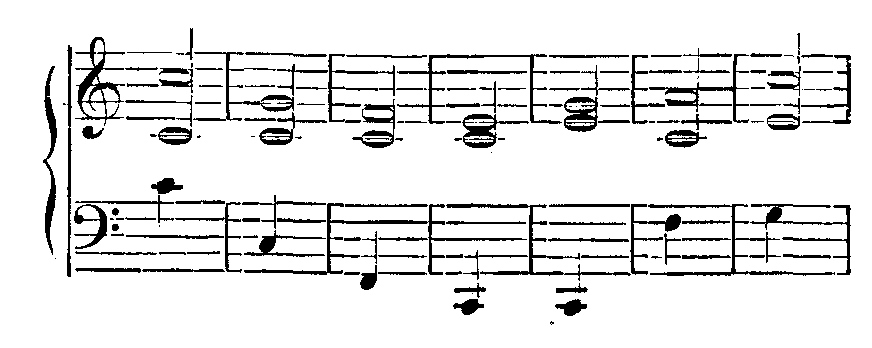
DIE STÖRUNGEN
DES
ZUSAMMENKLANGES.
KOMBINATIONSTÖNE UND SCHWEBUNGEN, KONSONANZ UND
DISSONANZ.
Siebenter Abschnitt.
Die Kombinationstöne.
In der ersten Abteilung dieses Buches ist das Gesetz ausgesprochen und fortdauernd angewendet worden, daß die schwingenden Bewegungen der Luft und anderer elastischer Körper, welche durch mehrere gleichzeitig wirkende Tonquellen hervorgebracht werden, immer die genaue Summe der einzelnen Bewegungen sind, welche die einzelnen Tonquellen hervorbringen. Dieses Gesetz ist von außerordentlicher Wichtigkeit für die Akustik, weil es die Betrachtung zusammengesetzter Fälle ganz auf die der einfachen zurückführt; aber es ist zu beachten, daß es in voller Strenge nur gilt, wo die Schwingungen an allen Stellen des Luftraumes und der tönenden elastischen Körper von unendlich kleiner Größe sind, wo also die Dichtigkeitsänderungen der elastischen Körper so klein sind, daß sie, verglichen mit der ganzen Dichtigkeit derselben Körper, nicht in Betracht kommen, und ebenso die Verschiebungen der schwingenden Teilchen verschwindend klein sind, verglichen mit den Dimensionen der ganzen elastischen Massen. Nun sind allerdings in den praktischen Anwendungen dieses Gesetzes auf tönende Körper die Schwingungen fast immer sehr klein, und dem unendlich kleinen nahe genug, daß jenes Gesetz mit sehr großer Annäherung auch für die wirklichen Schallschwingungen der musikalischen Töne richtig bleibt, und bei weitem der größte Teil der Erscheinungen aus jenem Gesetze mit der Beobachtung übereinstimmend gefolgert werden kann. Indessen gibt es doch gewisse Erscheinungen, die davon herrühren, daß jenes Gesetz für die zwar sehr kleinen, aber doch nicht unendlich kleinen Schwingungen elastischer Körper nicht ganz genau zutrifft1). Eine dieser Erscheinungen, die uns hier interessiert, sind die Kombinationstöne, zuerst entdeckt 1740 von Sorge2), einem deutschen Organisten, später allgemeiner bekannt; geworden, aber zum Teil mit irrigen Angaben über ihre Höhe, durch den italienischen Violinisten Tartini, nach welchem sie auch oft Tartini'sche Töne genannt werden.
1) Helmholtz, über Kombinationstöne in Poggendorffs Annalen Bd. XCIX, S. 497. — Monatsberichte der Berliner Akademie, 22. Mai 1856. Daraus ein Auszug in Beilage XII. [Wiss. Abh. Bd. I, S. 263.]
2) Vorgemach musikalischer Komposition.
Man hört diese Kombinationstöne, wenn zwei musikalische Töne von verschiedener Höhe gleichzeitig kräftig und gleichmäßig anhaltend angegeben werden. Die Höhe der Kombinationstöne ist im Allgemeinen verschieden sowohl von der der primären Töne, als auch von der ihrer harmonischen Obertöne. Bei Versuchen unterscheidet man sie daher von den letzteren einfach dadurch, daß die Kombinationstöne fehlen, wenn einer der primären Töne allein angegeben wird und jene erst auftreten, wenn beide primären Töne gleichzeitig angegeben werden. Die Kombinationstöne zerfallen in zwei Klassen. Die erste, von Sorge und Tartini entdeckte Klasse, welche ich Differenztöne genannt habe, ist dadurch charakterisiert, daß ihre Schwingungszahlen gleich sind den Differenzen zwischen den Schwingungszahlen der primären Töne. Die zweite Klasse, die Summationstöne, sind von mir entdeckt; ihre Schwingungszahlen sind gleich der Summe der Schwingungszahlen der primären Töne.
Sucht man die Kombinationstöne von zwei zusammengesetzten Klängen auf, so können sowohl deren Grundtöne als deren Obertöne mit einander sowohl Summationstöne als Differenztöne geben. Die Zahl der vorhandenen Kombinationstöne ist in solchem Falle also sehr groß. Doch ist zu bemerken, daß im Allgemeinen die Differenztöne stärker sind als die Summationstöne, und daß die stärkeren primären Tone auch die stärkeren Kombinationstöne geben. Ja die Kombinationstöne wachsen sogar in einem viel stärkeren Verhältnisse als die primären Töne, und nehmen auch schneller ab als diese. Da nun in musikalischen Klängen der Grundton meist an Stärke die Obertöne überwiegt, so sind es hauptsächlich die Kombinationstöne der beiden Grundtöne, und zwar deren Differenztöne, welche stärker als alle anderen in das Ohr fallen, und welche deshalb auch zuerst gefunden worden sind. Am leichtesten sind sie zu hören, wenn die beiden primären Töne um weniger als eine Oktave von einander abstehen; dann ist der Differenzton der Grundtöne tiefer als beide primären Töne. Um ihn zuerst zu hören, wähle man zwei Klänge, welche stark und anhaltend hervorgebracht werden können und ein rein gestimmtes harmonisches. Intervall bilden, das enger als eine Oktave ist. Man lasse erst den tieferen von beiden angeben, dann auch den höheren. Bei gehöriger Aufmerksamkeit wird man bemerken, daß in dem Augenblicke, wo die höhere Note hinzukommt, auch ein schwacher tieferer Ton hörbar wird, der eben der gesuchte Kombinationston ist. Bei einzelnen Instrumenten, z. B. dem Harmonium, kann man die Kombinationtöne auch durch passend abgestimmte Resonanzkugeln hörbarer machen. Hier sind sie schon in dem Luftraume des Instruments erzeugt. In anderen Fällen aber, wo sie nur im Ohre erzeugt werden, helfen die Resonanzkugeln wenig oder nichts.
Folgende Tafel gibt die ersten Differenztöne der gewöhnlichen
harmonischen Intervalle:
|
|
|
|
Kombinationston ist tiefer als der tiefere primäre Ton um |
| Oktave ..... |
|
|
Einklang |
| Quinte ...... |
|
|
Oktave |
| Quarte ...... |
|
|
Duodecime |
| Große Terz . . . |
|
|
2 Oktaven |
| Kleine Terz . . . |
|
|
2 Oktaven u. große Terz |
| Große Sexte . . . |
|
|
Quinte |
| Kleine Sexte . . . |
|
|
Grosse Sexte |
oder in Notenschrift, wobei die primären Töne durch halbe Noten, die Kombinationstöne durch Viertel angegeben sind:
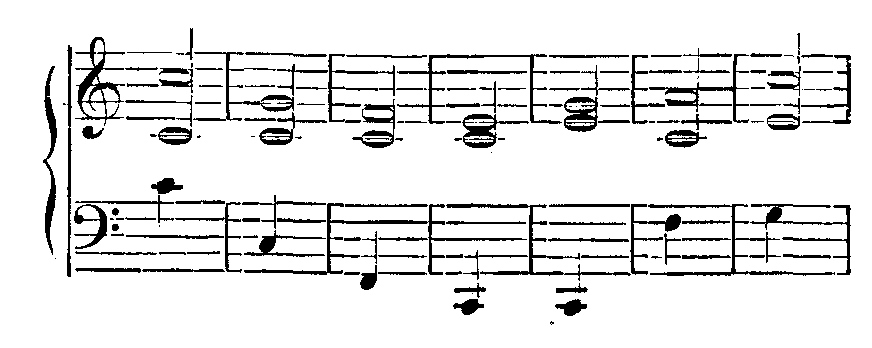
Nachdem man sich geübt hat, die Kombinationstöne reiner Intervalle und gehaltener Töne zu hören, lernt man sie auch bei disharmonischen Intervallen und bei den schnell verhallenden Tönen des Klaviers erkennen. Die der disharmonischen Intervalle werden dadurch schwerer erkennbar, daß sie in stärkeren oder schwächeren Schwebungen begriffen sind, wovon wir den Grund später erörtern werden. Die der schnell verhallenden Töne, wie die des Klaviers, sind eben nur im ersten Augenblicke stark genug, um deutlich gehört zu werden, und verhallen selbst schneller als die primären Töne. Auch sind sie im Allgemeinen bei den einfachen Tönen der Stimmgabeln und der gedackten Orgelpfeifen leichter zu hören, als bei zusammengesetzten Klängen, wo schon eine Menge anderer Nebentöne vorhanden sind. Letztere geben, wie schon erwähnt ist, auch noch eine Anzahl von Differenztönen der harmonischen Obertöne, die leicht die Aufmerksamkeit von dem Differenzton der Grundtöne ablenken. Dergleichen Kombinationstöne der Obertöne hört man namentlich bei der Violine und am Harmonium häufig.
Beispiel: Man nehme die große Terz c' e', Zahlenverhältnis 4:5. Der erste Differenzton ist l, d. h. C. Der erste harmonische Oberton von c' ist c" mit der Schwingungszahl 8. Dieser gibt mit e' die Differenz 3, d. h. g. Der erste Oberton von c' ist e" mit der Schwingungszahl 10, dieser gibt mit c' oder 4 die Differenz 6, d. h. g'. Dann geben c" und e" den Kombinationston 2, d. h. c. So erhalten wir also durch die ersten Obertöne schon die Reihe der Kombinationstöne 1, 3, 6, 2, oder C, g, g', c. Von diesen ist namentlich der Ton 3 oft leicht wahrzunehmen.
Diese mehrfachen Kombinationstöne sind gewöhnlich nur dann deutlich hörbar, wenn die primären Klänge deutlich hörbare harmonische Obertöne enthalten. Doch kann man nicht behaupten, daß erstere ganz fehlten, wo die letzteren fehlen; nur sind sie dann so schwach, daß das Ohr sie nicht leicht neben den starken primären Tönen und dem ersten Differenzton erkennt. Einmal läßt die Theorie schließen, daß sie schwach da seien; und die Schwebungen unreiner harmonischer Intervalle, von denen später zu sprechen ist, geben ebenfalls ihr Dasein zu erkennen. Man kann in diesen Fällen mit Hallstroem3) die Entstehung der mehrfachen Kombinationstöne so darstellen, als wenn der erste Differenzton, der Kombinationston erster Ordnung, mit den primären Tönen selbst wieder Differenztöne gibt, Kombinationstöne zweiter Ordnung, diese wieder neue mit den primären Tönen und den Tönen erster Ordnung und so fort.
3) Poggendorff's Annalen Bd. XXIV, S. 438.
Beispiel: Setzen wir wieder voraus, daß zwei einfache Töne im Verhältnis 4:5, nämlich c' und e' zusammenklingen, so ist der Differenzton erster Ordnung l oder C. Dieser gibt mit den primären Tönen 4 und 5 die Differenztöne zweiter Ordnung 3 und 4, g und ein zweites c'. Der neue Ton 3 gibt mit den primären Tonen 4 und 5 die Töne dritter Ordnung l und 2, C und c, mit dem Tone erster Ordnung l den Ton vierter Ordnung 2, nämlich ein zweites c u. s. w. Die Töne verschiedener Ordnung, welche in diesem Beispiele unter Voraussetzung absolut reiner Stimmung zusammenfallen, tun es nicht mehr vollständig, wenn die Stimmung des primären Intervalls nicht absolut rein ist; dann entstehen Schwebungen, wie sie durch die Anwesenheit dieser Töne gefordert werden. Davon später mehr.
Hier folgen die Systeme der Differenztöne verschiedener Ordnungen für verschiedene Intervalle. Die primären Töne sind in halben Noten, die Kombinationstöne erster Ordnung in Vierteln, die zweiter Ordnung in Achteln u. s. w. geschrieben. Dieselben Töne entstehen bei zusammengesetzten Klängen auch als Kombinationstöne der Obertöne.


Kleine Terz. Grosse Sexte. Kleine Sexte.
Die zweite Art der Kombinationstöne, welche ich Summationstöne genannt habe, ist im Allgemeinen von viel geringerer Tonstärke als die Differenztöne, und nur bei besonders günstigen Gelegenheiten, namentlich am Harmonium und an der mehrstimmigen Sirene, leichter zu hören. Es kommen fast nur die ersten derselben zur Wahrnehmung, deren Schwingungszahl gleich der Summe der Schwingungszahlen der primären Töne ist. Es können natürlich auch Summationstöne der harmonischen Obertöne existieren. Da ihre Schwingungszahl immer gleich der Summe der Schwingungszahlen der primären Töne ist, so sind sie stets höher als diese. Für die einfachen Intervalle ergeben sie sich aus folgender Übersicht:
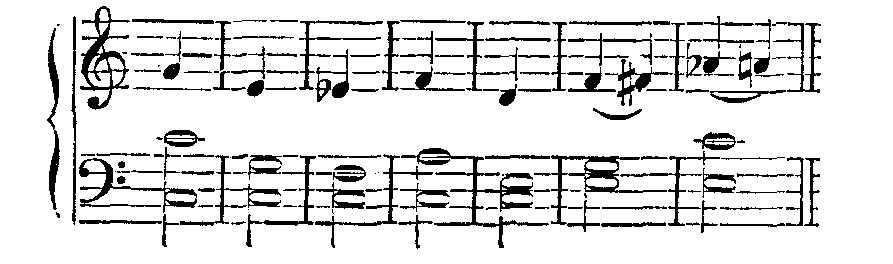
Man hat die Kombinationstöne früher für rein subjektiv gehalten und geglaubt, sie entständen erst im Ohre selbst. Man kannte nur die Differenztöne und stellte diese mit den Schwebungen zusammen, welche je zwei zusammenklingende Töne von wenig verschiedener Tonhöhe zu geben pflegen, eine Erscheinung, die wir in den nächsten Abschnitten noch näher untersuchen werden. Man glaubte, wenn solche Schwebungen schnell genug wären, könnten die einzelnen Schwellangen der Tonstärke, gerade so wie es ebenso viele gewöhnliche einfache Luftstöße tun würden, die Empfindung eines neuen Tones hervorbringen, dessen Schwingungszahl der Zahl der Schwebungen gleich sei. Diese Ansicht erklärt aber erstens nicht die Entstehung der Summationstöne, sondern nur die der Differenztöne; zweitens läßt sich nachweisen, daß unter Umständen die Kombinationstöne objektiv existieren, unabhängig vom Ohr, welches die Schwebungen zu einem neuen Tone zusammen addieren soll; und drittens läßt sich diese Ansicht nicht mit dem durch alle übrigen Erfahrungen bestätigten Gesetze vereinigen, daß das Ohr nur diejenigen Töne empfindet, welche einfachen pendelartigen Bewegungen der Luft entsprechen.
Es läßt sich in der Tat ein anderer Grund für die Entstehung der Kombinationstöne nachweisen, der schon oben im Allgemeinen bezeichnet ist. Wenn nämlich irgendwo die Schwingungen der Luft oder eines anderen elastischen Körpers, der von beiden primären Tönen gleichzeitig in Bewegung gesetzt wird, so heftig werden, daß die Schwingungen nicht mehr als unendlich klein betrachtet werden können, da müssen, wie die mathematische Theorie nachweist, solche Schwingungen der Luft entstehen, deren Tonhöhe den Kombinationstönen entspricht.
Einzelne Instrumente liefern besonders starke Kombinationstöne.
Die Bedingung für ihre Erzeugung ist, daß dieselbe Luftmasse
von beiden Tönen in heftige Erschütterung versetzt wird. Dies
geschieht am stärksten in der mehrstimmigen Sirene, in welcher dieselbe
rotierende Scheibe zwei oder mehrere Löcherreihen enthält, die
aus demselben Windkasten gleichzeitig angeblasen werden4). Die
Luft des Windkastens ist verdichtet, so oft die Löcher geschlossen
sind; wenn sie geöffnet werden, stürzt ein großer Teil
derselben in das Freie, es tritt eine beträchtliche Druckverminderung
ein. So gerät die Luftmasse im Windkasten und zum Teil selbst im Blasebalg,
wie man an diesem leicht fühlen kann, in heftige Schwingungen. Werden
zwei Löcherreihen angeblasen, so entstehen Schwingungen in der Luftmasse
des Windkastens, die beiden Tönen entsprechen; und durch jede Reihe
von Öffnungen wird nicht ein gleichmäßig zumessender Luftstrom
entleert, sondern ein Luftstrom, der durch den anderen Ton schon in Schwingungen
versetzt ist. Die Kombinationstöne sind unter diesen Umständen
außerordentlich stark, fast ebenso stark wie die primären Töne.
Daß sie hierbei objektiv in der Luftmasse existieren, kann man durch
schwingende Membranen nachweisen, welche mit den Kombinationstönen
im Einklang sind. Solche Membranen werden in Mitschwingung versetzt, sobald
man beide primäre Töne zugleich angibt, nicht aber, wenn man
nur einen oder den anderen primären Ton angibt. Namentlich sind in
diesem Falle auch die Summationstöne so stark, daß sie Akkorde,
in denen Terzen oder kleine Sexten vorkommen, äußerst widrig
machen. Statt der Membranen ist es bequemer, die Resonatoren zu gebrauchen,
welche ich oben für die Untersuchung der harmonischen Obertöne
empfohlen habe. Auch diese können nur einen Ton verstärken, dessen
entsprechende pendelartige Schwingung im Luftraum vorhanden ist, und nicht
einen Ton, der nur in der Empfindung des Ohres existiert; man kann sie
deshalb gebrauchen, um zu ermitteln, ob ein Kombinationston objektiv vorhanden
ist. Sie sind sehr viel empfindlicher als die Membranen und geeignet, auch
sehr schwache objektive Töne deutlich erkennen zu lassen.
4) Ein solches Instrument wird im nächsten Abschnitte
genauer beschrieben werden.
Ähnlich wie bei der Sirene sind die Verhältnisse im Harmonium. Auch hier ist ein gemeinsamer Windraum vorhanden, und wenn zwei Tasten angeschlagen werden, haben wir zwei Öffnungen, welche durch die Zungen rhythmisch geöffnet und geschlossen werden. Auch hier wird die Luft in dem gemeinsamen Behälter durch beide Töne stark erschüttert, und durch jede Öffnung Luft geblasen, die von der anderen Zunge her schon in schwingende Bewegung gesetzt ist. Es sind deshalb auch bei diesem Instrumente die Kombinationstöne objektiv vorhanden und verhältnismäßig sehr deutlich, aber sie sind lange nicht so stark, wie in der Sirene, wohl weil der Windkasten im Verhältnis zu den Öffnungen außerordentlich viel größer ist und deshalb während der kurzen Eröffnung eines Windlochs durch die schwingende Zunge nicht so viel Luft herausstürzen kann, um den Druck erheblich zu vermindern. Auch am Harmonium hört man die Kombinationstöne durch gleichgestimmte Resonatoren sehr deutlich verstärkt, namentlich den ersten und zweiten Differenzton und den ersten Summationston. Indessen habe ich mich durch besondere Versuche überzeugt, daß auch bei dem genannten Instrumente der größere Teil der Stärke des Kombinationstons erst im Ohre entsteht. Ich habe die Windleitungen in dem Instrumente so eingerichtet, daß ein Ton von den unteren mit dem Fuße getretenen Bälgen aus mit Luft versehen wurde, ein zweiter von dem vorher vollgepumpten und durch Ausziehen des sogenannten Expressionszuges nachher abgeschlossenen Reservebalge, und fand die Kombinationstöne nicht eben viel schwächer als bei der gewöhnlichen Anordnung. Wohl aber war der objektive Teil derselben, welcher durch die Resonatoren verstärkt werden kann, viel schwächer. Man wird nach der oben gegebenen Übersicht der Kombinationstöne leicht die Tasten finden können, welche man anschlagen muß, um einen Kombinationston hervorzubringen, der durch eine gegebene Resonanzröhre verstärkt wird.
Wenn dagegen die Erregungsstellen der beiden Töne ganz von einander getrennt sind, und keinen mechanischen Zusammenhang haben, wenn also z. B. zwei Singstimmen, oder zwei einzelne Blasinstrumente, oder zwei Violinen den Ton angeben, ist die Verstärkung der Kombinationstöne durch die Resonanzröhren schwach und zweifelhaft. Hier ist also im Luftraum eine dem Kombinationstone entsprechende pendelartige Schwingung nicht deutlich wahrnehmbar, und wir müssen schließen, daß die Kombinationstöne, die zuweilen recht kräftig sind, wirklich erst im Ohre entstehen. Aber nach der Analogie der früheren Fälle dürfen wir auch hierbei wohl annehmen, daß es zunächst die äußeren schwingenden Teile des Ohres, namentlich das Trommelfell und die Gehörknöchelchen sind, in denen die Schwingungen hinreichend kräftig zusammenwirken, um Kombinationstöne zu erzeugen, so daß also die den Kombinationstönen entsprechenden Schwingungen in diesen Teilen des Ohres wirklich objektiv bestehen mögen, ohne daß sie im Luftraum objektiv vorkommen. Eine kleine Verstärkung des Kombinationstons durch den entsprechenden Resonator kann daher wohl auch in diesem Falle dadurch entstehen, daß das Trommelfell solche Schwingungen, die dem Kombinationstone entsprechen, an die Luftmasse des Resonators abgibt.
In der Tat sind nun auch in der Konstruktion der äußeren schalleitenden Teile des Ohres gewisse Verhältnisse vorhanden, welche besonders günstig für die Erzeugung von Kombinationstönen erscheinen. Einmal kommt der unsymmetrische Bau des Trommelfells in Betracht. Die nach außen konvexen Radialfasern desselben werden eine stärkere Spannungsänderung erleiden, wenn sie eine Schwingung von mäßiger Amplitude nach innen machen, als wenn die Schwingung nach außen geht. Zu dem Ende braucht die Amplitude der Schwingung nur einen nicht allzu kleinen Bruchteil der geringen Wölbungstiefe des Bogens dieser Radialfasern auszumachen. Unter diesen Umständen entstehen Abweichungen von der einfachen Superposition der Schwingungen schon bei viel kleineren Amplituden, als dieses der Fall ist, wenn der schwingende Körper nach beiden Seiten hin symmetrisch gebaut ist5).
5) Siehe meinen oben zitierten Aufsatz über Kombinationstöne und Beilage XII. Bei asymmetrisch gebauten schwingenden Körpern sind die Störungen der ersten Potenz der Amplitude proportional, bei symmetrisch gebauten erst der zweiten Potenz dieser immerhin kleinen Größe.
Noch wichtiger erscheint mir aber namentlich bei starken Tönen, die lose Beschaffenheit des Hammer-Amboßgelenks zu sein. Wird der Hammerstiel mit dem Trommelfell einwärts getrieben, so muß der Amboß und Steigbügel dieser Bewegung unbedingt folgen, nicht aber, wenn darauf die Auswärtsbewegung des Hammerstiels folgt, wobei die Sperrzähne der beiden Knochen von einander loslassen können. Dann können die Knochen an einander klirren. Solches Klirren meine ich in meinem eigenen Ohre immer zu hören, so oft ein sehr starker, namentlich tiefer Ton meinem Ohre zugeleitet wird, auch wenn dies z. B. der Ton einer zwischen den Fingern gehaltenen Stimmgabel ist, an der sich unbedingt nichts Klirrendes befindet.
Dieses eigentümliche Gefühl mechanischen Schwirrens im Ohre ist mir schon längst auffallend gewesen, wenn zwei starke und reine Sopranstimmen Terzengänge ausführen, wobei dann der Kombinationston sehr deutlich herauskommt. Stellen sich die Phasen der beiden Töne so zu einander, daß nach jeder vierten Oszillation des tieferen, nach jeder fünften des höheren eine starke Auswärtsschwingung des Trommelfells erfolgt, stark genug, um ein momentanes Loslassen im Hammer-Amboßgelenk zu verursachen, so wird sich dadurch eine Reihe von Stößen zwischen den beiden Knochen erzeugen, welche bei fester Verbindung und regelnlässiger Schwingung fehlen würden, und welche zusammengenommen gerade den ersten Differenzton jenes Terzenintervalls erzeugen würden. Ähnlich bei anderen Intervallen.
Zu bemerken ist übrigens, daß dieselben Umstände in der Konstruktion eines schwingenden Körpers, welche ihn geeignet machen, Kombinationstöne hören zu lassen, wenn er von zwei verschieden hohen Tonwellenzügen erregt wird, auch bewirken müssen, daß ein einzelner einfacher Ton in ihm Schwingungen erregen muß, die seinen harmonischen Obertönen entsprechen, gleichsam als wenn dieser Ton dann mit sich selbst Summationstöne bildete.
Eine einfachen pendelartigen Schwingungen entsprechende einfach periodische Kraft erregt nämlich nur dann und so lange einfache Sinusschwingungen in einem elastischen Körper, auf den sie wirkt, als die durch die Abweichungen des erregten Körpers von seiner Gleichgewichtslage wachgerufenen elastischen Kräfte diesen Abweichungen selbst proportional bleiben, was bei verschwindend kleiner Größe derselben immer der Fall ist. Werden die Amplituden der Schwingungen so groß, daß merkliche Abweichungen von dieser Proportionalität eintreten, so treten zu den Schwingungen des erregenden Tones noch solche hinzu, welche seinen harmonischen Obertonen entsprechen. Daß solche harmonische Obertöne bei starker Erregung von Stimmgabeln zuweilen vorkommen, habe ich schon S. 95 angeführt. Ich habe neuerdings diese Versuche mit sehr tiefen Gabeln wiederholt. Bei einer solchen von 64 Schwingungen konnte ich mit geeigneten Resonatoren die Obertöne bis zum fünften hören, wenn sie stark angeschlagen war, wobei sie Schwingungen machte, deren Amplitude fast einen Zentimeter betrug. Bei so großer Breite der Schwingungen eines scharfkantigen Körpers, wie es die Gabelzinken sind, müssen in der umgebenden Luft Wirbelbewegungen entstehen, die erheblich von dem Gesetze der einfachen Schwingungen abweichen. Dagegen schwinden diese Obertöne beim Austönen der Gabel lange vor dem doch auch nur sehr schwach hörbaren tiefen Grundtone derselben, entsprechend der von uns gemachten Voraussetzung, daß sie auf Störungen beruhen, die von der Größe der Amplitude abhängen.
Herr R. Koenig6) hat mit einer Reihenfolge stimmbarer Gabeln, die mit entsprechenden gut resonierenden Kästen versehen waren und sehr mächtige Töne gaben, die Schwebungen und Kombinationstöne untersucht und dabei gefunden, daß diejenigen unter den letzteren am stärksten hervortreten, welche der Differenz des einen Tons mit dem nächstgelegenen Oberton des nächsten entsprechen, wobei zum Teil sich die Obertöne bis zum achten hinauf (wenigstens in der Zahl der Schwebungen) geltend machten. Er hat leider nicht angegeben, wie weit er die entsprechenden Obertöne durch Resonatoren einzeln erkennen konnte.
Welche wichtige Rolle die Kombinationstöne bei der Akkordbildung spielen, wird sich später ergeben. Ehe wir dazu übergehen können, müssen wir ein zweites Phänomen des Zusammenklanges zweier Töne untersuchen, nämlich die Schwebungen.