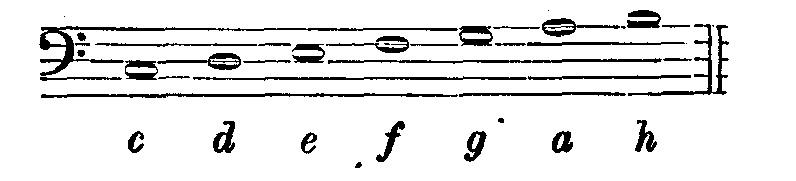
DIE ZUSAMMENSETZUNG
DER
SCHWINGUNGEN.
OBERTÖNE UND KLANGFARBEN.
Erster Abschnitt
Von der Schallempfindung im Allgemeinen.
Sinnliche Empfindungen kommen zu Stande, indem äußere Reizmittel auf die empfindlichen Nervenapparate unseres Körpers einwirken und diese in Erregungszustand versetzen. Die Art der Empfindung ist verschieden, teils nach dem Sinnesorgane, welches in Anspruch genommen worden ist, teils nach der Art des einwirkenden Reizes. Jedes Sinnesorgan vermittelt eigentümliche Empfindungen, welche durch kein anderes erregt werden können, das Auge Lichtempfindungen, das Ohr Schauempfindungen, die Haut Tastempfindungen. Selbst wenn dieselben Sonnenstrahlen, welche dem Auge die Empfindung des Lichts erregen, die Haut treffen und deren Nerven erregen, so werden sie hier doch nur als Wärme, nicht als Licht empfunden, und ebenso können die Erschütterungen elastischer Körper, welche das Ohr hört, auch von der Haut empfunden werden, aber nicht als Schall, sondern als Schwirren. Schallempfindung ist also die dem Ohre eigentümliche Reaktionsweise gegen äußere Reizmittel, sie kann in keinem anderen Organe des Körpers hervorgebracht werden, und unterscheidet sich durchaus von allen Empfindungen aller übrigen Sinne.
Da wir uns hier die Aufgabe gestellt haben, die Gesetze der Gehörempfindungen zu studieren, so wird es unsere erste Aufgabe sein zu untersuchen, wie viel verschiedene Arten von Empfindungen unser Ohr erzeugen kann, und welche Unterschiede des äußeren Erregungsmittels, nämlich des Schalls, diesen Unterschieden der Empfindung entsprechen.
Der erste und Hauptunterschied verschiedenen Schalls, den unser Ohr auffindet, ist der Unterschied zwischen Geräuschen und musikalischen Klängen. Das Sausen, Heulen und Zischen des Windes, das Plätschern des Wassers, das Rollen und Rasseln eines Wagens sind Beispiele der ersten Art, die Klänge sämtlicher musikalischen Instrumente Beispiele der zweiten Art des Schalls. Zwar können Geräusche und Klänge in mannigfach wechselnden Verhältnissen sich vermischen und durch Zwischenstufen in einander übergehen, ihre Extreme sind aber weit von einander getrennt.
Um das Wesen des Unterschieds zwischen Klängen und Geräuschen zu ermitteln, genügt in den meisten Fällen schon eine aufmerksame Beobachtung des Ohres allein, ohne daß es durch künstliche Hilfsmittel unterstützt zu werden braucht. Es zeigt sich nämlich im Allgemeinen, daß im Verlaufe eines Geräusches ein schneller Wechsel verschiedenartiger Schallempfindungen eintritt. Man denke an das Rasseln eines Wagens auf Steinpflaster, das Plätschern und Brausen eines Wasserfalls oder der Meereswogen, das Rauschen der Blätter im Walde. Hier haben wir überall einen raschen und unregelmäßigen, aber deutlich erkennbaren Wechsel stoßweise aufblitzender verschiedenartiger Laute. Beim Heulen des Windes ist der Wechsel langsam, der Schall zieht sich langsam und allmälig in die Höhe und sinkt dann wieder. Mehr oder weniger gut gelingt die Trennung verschiedenartiger unruhig wechselnder Laute auch bei den meisten anderen Geräuschen; wir werden später ein Hilfsmittel kennen lernen, die Resonatoren, mittels dessen diese Unterscheidung dem Ohre beträchtlich erleichtert wird. Ein musikalischer Klang dagegen erscheint dem Ohre als ein Schall, der vollkommen ruhig, gleichmäßig und unveränderlich dauert, so lange er eben besteht, in ihm ist kein Wechsel verschiedenartiger Bestandteile zu unterscheiden. Ihm entspricht also eine einfache und regelmäßige Art der Empfindung, während in einem Geräusche viele verschiedenartige Klangempfindungen unregelmäßig gemischt und durch einander geworfen sind. In der Tat kann man Geräusche ans musikalischen Klängen zusammensetzen, wenn man z. B. sämtliche Tasten eines Klaviers innerhalb der Breite von einer oder zwei Oktaven gleichzeitig anschlägt. Hiernach ist es klar, daß die musikalischen Klänge die einfacheren und regelmäßigeren Elemente der Gehörempfindungen sind, und daß wir an ihnen zunächst die Gesetze und Eigentümlichkeiten dieser Empfindungen zu studieren haben.
Wir gelangen jetzt zu der weiteren Frage: welcher Unterschied in dem äußeren Erregungsmittel der Gehörempfindungen bedingt den Unterschied von Geräusch und Klang ? Das normale und gewöhnliche Erregungsmittel für das menschliche Ohr sind Erschütterungen der umgebenden Luftmasse. Die unregelmäßig wechselnde Empfindung des Ohrs bei den Geräuschen lässt uns schließen, daß bei diesen auch die Erschütterung der Luft eine unregelmäßig sich verändernde Art der Bewegung sein müsse, daß den musikalischen Klängen dagegen eine regelmäßige in gleich-massiger Weise andauernde Bewegung der Luft zu Grunde liege, welche wiederum erregt sein muss durch eine ebenso regelmäßige Bewegung des ursprünglich tönenden Körpers, dessen Stöße die Luft dem Ohre zuleitet.
Die Art solcher regelmäßiger Bewegungen, welche einen musikalischen Klang hervorbringen, haben nun die physikalischen Untersuchungen genau kennen gelehrt. Es sind dies Schwingungen, d. h. hin- und hergehende Bewegungen der tönenden Körper, und diese Schwingungen müssen regelmäßig periodisch sein. Unter einer periodischen Bewegung verstehen wir eine solche, welche nach genau gleichen Zeitabschnitten immer in genau derselben Weise wiederkehrt. Die Länge der gleichen Zeitabschnitte, welche zwischen einer und der nächsten Wiederholung der gleichen Bewegung verfließen, nennen wir die Schwingungsdauer oder die Periode der Bewegung. Welcher Art die Bewegung des bewegten Körpers während der Dauer einer Periode ist, ist dabei ganz gleichgültig. Um den Begriff der periodischen Bewegung an bekannten Beispielen zu erläutern, führe ich an die Bewegung des Pendels einer Uhr, die Bewegung eines Steins, der an einem Faden befestigt mit gleichbleibender Geschwindigkeit im Kreise herumgeschwungen wird, die Bewegung eines Hammers, der von dem Räderwerk einer Wassermühle nach regelmäßigen Zwischenzeiten gehoben wird und wieder fällt. Alle diese Bewegungen, so verschieden sie sich übrigens auch gestalten mögen, sind periodisch in dem angeführten Sinne. Die Dauer ihrer Periode, welche in diesen Fällen meist eine oder mehrere Sekunden beträgt, ist aber verhältnismäßig lang, verglichen mit den viel kürzeren Perioden der tönenden Schwingungen, von denen bei den tiefsten Tönen mindestens 30 auf eine Sekunde kommen, und deren Anzahl bis auf viele Tausende in der Sekunde steigen kann.
Unserer Definition der periodischen Bewegung gemäß können wir nun die gestellte Frage so beantworten: Die Empfindung eines Klanges wird durch schnelle periodische Bewegungen der tönenden Körper hervorgebracht, die eines Geräusches durch nicht periodische Bewegungen.
Die tönenden Schwingungen fester Körper können wir sehr häufig mit dem Auge erkennen. Wenn auch die Schwingungen zu schnell vor sich gehen, als daß wir jeder einzelnen mit dem Auge folgen könnten, so erkennen wir doch leicht an einer tönenden Saite, oder Stimmgabel, oder an der Zunge einer Zungenpfeife, daß dieselben in lebhafter hin- und hergehender Bewegung zwischen zwei festen Grenzlagen begriffen sind, und das regelmäßige und scheinbar ruhig fortbestehende Bild, welches ein solcher schwingender Körper trotz seiner Bewegung dem Auge darbietet, lässt auf die Regelmäßigkeit seiner Hin- und Hergänge schließen. In anderen Fällen können wir die schwingende Bewegung der tönenden festen Körper fühlen. So fühlt der Blasende die Schwingungen der Zunge am Mundstück der Klarinette, Oboe, des Fagotts, oder die Schwingungen seiner eigenen Lippen im Mundstück der Trompete und Posaune.
Unserem Ohre werden nun die Erschütterungen, welche von den tönenden Körpern ausgehen, in der Regel erst durch Vermittelung der Luft zugetragen. Auch die Luftteilchen müssen periodisch sich wiederholende Schwingungen ausführen, um in unserem Öhre die Empfindung eines musikalischen Klanges hervorzubringen. Dies ist auch in der Tat der Fall, obgleich in der alltäglichen Erfahrung der Schall zunächst als ein Agens erscheint, welches gleichmäßig im Luftraume vorschreitet, indem es sich immer weiter und weiter ausbreitet. Wir müssen aber hier unterscheiden zwischen der Bewegung der einzelnen Luftteilchen selbst
— diese ist periodisch hin- und hergehend innerhalb enger Grenzen
— und der Ausbreitung der Erschütterung des Schalls; diese letztere
ist es, welche fortdauernd vorwärts schreitet, indem immer neue und
neue Luftteilchen in den Kreis der Erschütterung gezogen werden.
Es ist dies eine Eigentümlichkeit aller sogenannten Wellenbewegungen. Man denke sich in eine eben ruhige Wasserfläche einen Stein geworfen. Um den getroffenen Punkt der Fläche bildet sich sogleich ein kleiner Wellenring, welcher nach allen Richtungen hin gleichmäßig fortschreitend sich zu einem immer größer werdenden Kreise ausdehnt. Diesem Wellenringe entsprechend geht in der Luft von einem erschütterten Punkte der Schalt aus, und schreitet nach allen Richtungen fort, so weit die Grenzen der Luftmasse es erlauben. Der Vorgang in der Luft ist im Wesentlichen ganz derselbe wie auf der Wasserfläche, der Hauptunterschied ist der, daß der Schall in dem räumlich ausgedehnten Luftmeere nach allen Seiten kugelförmig sich ausbreitend fortschreitet, während die Wellen an der Oberfläche des Wassers nur ringförmig fortschreiten können. Den Bergen der Wasserwellen entsprechen bei den Schallwellen Schichten, in denen die Luft verdichtet ist, den Wellentälern verdünnte Schichten. An der freien Wasseroberfläche kann die Masse nach oben ausweichen, wo sie sich zusammendrängt, und so die Berge bilden. Im Inneren des Luftmeeres muss sie sich verdichten, weil sie nicht ausweichen kann.
Die Wasserwellen also schreiten beständig vorwärts ohne umzukehren; aber man muss nicht glauben, daß die Wasserteilchen, aus denen die Wellen zusammengesetzt sind, eine ähnliche fortschreitende Bewegung haben wie die Wellen selbst. Die Bewegungen der Wasserteilchen längs der Oberfläche des Wassers können wir leicht sichtbar machen, indem wir ein Hölzchen auf dem Wasser schwimmen lassen. Ein solches macht die Bewegungen der benachbarten Wasserteilchen vollständig mit. Nun wird ein solches Hölzchen von den Wellenringen nicht mitgenommen, sondern nur auf und ab geschaukelt, und bleibt schließlich an der Stelle ruhen, an der es sich zuerst befand. Wie das Hölzchen, so auch die benachbarten Wasserteilchen. Wenn der Wellenring bei ihnen ankommt, werden sie in Schwankungen versetzt; wenn er vorübergezogen ist, sind sie wieder an ihrer alten Stelle und bleiben nun in Ruhe, während der Wellenring zu immer neuen Stellen der Wasserfläche fortschreitet und diese in Bewegung setzt. Es werden also die Wellen, welche über die Wasseroberfläche hinziehen, fort und fort ans neuen Wasserteilchen aufgebaut, so daß dasjenige, was als Welle fortrückt, nur die Erschütterung, die veränderte Form der Oberfläche ist, während die einzelnen Wasserteilchen in vorübergehenden Schwankungen hin- und hergehen, sich aber nie weit von ihrem ersten Platze entfernen.
Noch deutlicher zeigt sich dasselbe Verhältnis bei den Wellen eines Seils oder einer Kette. Man nehme einen biegsamen Faden von einigen Fuß Länge oder ein dünnes Metallkettchen, halte es an einem Ende und lasse das andere herabhängen, so daß der Faden nur durch seine Schwere gespannt ist. Nun bewege man die Hand, die es hält, schnell ein wenig nach einer Seite und wieder zurück. Es wird die Ausbiegung, die wir am oberen Ende des Fadens durch die Bewegung der Hand hervorgebracht haben, als eine Art Welle an ihm herablaufen, so daß immer tiefere und tiefere Teile des Fadens sich seitwärts ausbiegen, während die oberen wieder in die gestreckte Ruhelage zurückkehren, und doch ist es deutlich, daß, während die Welle nach unten hin abläuft, jeder einzelne Teil des Fadens nur horizontal hin- und herschwanken kann, und keineswegs die abwärts schreitende Bewegung der Welle teilt.
Noch vollkommener gelingt ein solcher Versuch an einem langen elastischen, schwach gespannten Faden, z. B. einer dicken Kautschukschnur, oder einer Messingspiralfeder von 8 bis 12 Fuß Länge, deren eines Ende befestigt ist, während man das andere in der Hand hält. Die Hand kann hier leicht Wellen erregen, welche in sehr regelmäßiger Weise nach dem anderen Ende des Fadens ablaufen, dort reflektiert werden und wieder zurückkommen. Auch hier ist es deutlich, daß es kein Teil der Schnur selbst sein kann, welcher hin- und herläuft, sondern daß immer andere und andere Teile der Schnur die fortschreitende Welle zusammensetzen. An diesen Beispielen wird der Leser sich eine Vorstellung bilden können von einer solchen Art der Bewegung, wie die des Schalls ist, bei welcher die materiellen Teilchen des bewegten Körpers nur periodische Schwingungen ausführen, während die Erschütterung selbst fortdauernd vorwärts schreitet.
Kehren wir zu der Wasserfläche zurück. Wir haben vorausgesetzt, daß ein Punkt derselben von einem Steine getroffen und erschüttert worden sei. Die Erschütterung hat sich in Form eines Wellenringes über die Wasserfläche ausgebreitet, ist zu dem schwimmenden Hölzchen gekommen und hat dieses in Schwankungen versetzt. So ist also mittels der Wellen die Erschütterung, welche der Stein an einem Punkte der Wasserfläche erregt hatte, dem Hölzchen, welches an einem anderen Punkte derselben Fläche sich befand, mitgeteilt worden. Von ganz ähnlicher Art ist der Vorgang in dem uns umgebenden Luftmeere. Statt des Steines setze man einen tönenden Körper, der die Luft erschüttert, statt des Hölzchens das menschliche Ohr, an welches die Erschütterungswellen der Luft anschlagen und dessen bewegliche Teile sie dabei in Bewegung setzen. Die Luftwellen, welche von einem tönenden Körper ausgehen, übertragen die Erschütterung auf das menschliche Ohr gerade ebenso, wie das Wasser sie von dem Stein auf den schwimmenden Körper überträgt.
Hiernach wird es leicht ersichtlich sein, wie ein in periodischer Schwingung begriffener Körper auch die Luftteilchen in eine periodische Bewegung setzen muss. Ein lallender Stein gibt der Wasserfläche nur einen einzelnen Stoß. Nun denke man sich aber statt des einen Steines etwa eine regelmäßige Reihe von Tropfen aus einem Gefäße mit enger Mündung in das Wasser fallend. Jeder Tropfen wird eine Ringwelle erregen, jede Ringwelle wird über die Wasserfläche ganz ebenso wie ihre Vorgängerin hinlaufen, und wie sie dieser folgte, werden ihr ihre Nachfolgerinnen folgen. So wird auf der Wasserfläche eine regelmäßige Reihe konzentrischer Ringe entstehen und sich ausbreiten. So viel Tropfen in der Sekunde in das Wasser fallen, so viel Wellen werden auch in der Sekunde unser schwimmendes Hölzchen treffen, und so viel Male wird dieses auf und ab geschaukelt werden, also eine periodische Bewegung ausführen, deren Periode gleich ist den Zeitabschnitten, in denen die Tropfen fallen. In derselben Weise bringt in der Luft ein periodisch bewegter tönender Körper eine ähnliche periodische Bewegung zunächst der Luftmasse, dann des Trommelfells in unserem Ohre hervor, deren Schwingungsdauer der des tönenden Körpers gleich sein muss.
Nachdem wir die erste Haupteinteilung des Schalls in Geräusche und Klänge besprochen, und die den Klängen zukommende Luftbewegung im Allgemeinen beschrieben haben, wenden wir uns zu den besonderen Eigentümlichkeiten, durch welche wiederum die Klänge sich von einander unterscheiden. Wir kennen drei Unterschiede der Klänge, wenn wir zunächst nur an solche Klänge denken, wie sie einzeln von unseren gewöhnlichen musikalischen Instrumenten hervorgebracht werden, und Zusammenklänge verschiedener Instrumente ausschließen. Klänge können sich nämlich unterscheiden:
Wir haben jetzt für diese drei Hauptunterschiede des Klanges auseinanderzusetzen, welche besonderen Eigentümlichkeiten der Schallbewegung ihnen entsprechen.
Was zunächst die Stärke der Klänge betrifft, so ist es leicht zu erkennen, daß diese mit der Breite (Amplitude) der Schwingungen des tönenden Körpers wächst und abnimmt. Wenn wir eine Saite anschlagen, sind ihre Schwingungen anfangs ausgiebig genug, daß wir sie sehen können; dem entsprechend ist ihr Ton anfangs am stärksten. Dann werden die sichtbaren Schwingungen immer kleiner und kleiner; in demselben Maße nimmt die Stärke des Tons ab. Dieselbe Beobachtung können wir an gestrichenen Saiten, den Zungen der Zungenpfeifen und vielen anderen tönenden Körpern machen. Die gleiche Folgerung müssen wir aus der Tatsache ziehen, daß die Stärke des Klanges abnimmt, wenn wir uns im Freien von dem tönenden Körper entfernen, während sich weder Tonhöhe noch Klangfarbe verändern. Mit der Entfernung ändert sich aber an den Luftwellen nur die Schwingungsamplitude der einzelnen Lufteilchen. Von dieser muss also die Stärke des Schalls abhängen, aber keine seiner anderen Eigenschaften1).
1) Mechanisch ist die Stärke der Schwingungen für Töne verschiedener Höhe durch ihre lebendige Kraft, d. h. durch das Quadrat der größten Geschwindigkeit zu messen, welche die schwingenden Teilchen erreichen. Aber das Ohr hat verschiedene Empfindlichkeit für Töne verschiedener Höhe, so daß ein für verschiedene Tonhöhen gültiges Maß der Intensität der Empfindung hierdurch nicht gewonnen werden kann.
Der zweite wesentliche Unterschied verschiedener Klänge beruht in ihrer Tonhöhe. Wir wissen schon aus der täglichen Erfahrung, daß Töne gleicher Tonhöhe von den verschiedensten Instrumenten mittels der verschiedensten mechanischen Vorgänge und in der verschiedensten Stärke erzeugt werden können. Die Luftbewegungen, welche hierbei entstehen, müssen alle periodisch sein, sonst erregen sie nicht die Empfindung eines musikalischen Klanges im Ohre. Innerhalb jeder einzelnen Periode kann die Bewegung sein, von welcher Art sie will; wenn nur die Dauer der Periode zweier Klänge gleich groß ist, so haben sie gleiche Tonhöhe. Also: Die Tonhöhe hängt nur ab von der Schwingungsdauer oder, was gleichbedeutend ist, von der Schwingungszahl. Wir pflegen die Sekunde als Zeiteinheit zu benutzen, und verstehen deshalb unter Schwingungszahl die Anzahl der Schwingungen, welche der tönende Körper in einer Zeitsekunde ausführt. Es ist selbstverständlich, daß wir die Schwingungsdauer finden, wenn wir die Sekunde durch die Schwingungszahl dividieren.
Die Klänge sind desto höher, je größer ihre Schwingungszahl oder je kleiner ihre Schwingungsdauer ist.
Die Zahl der Schwingungen solcher elastischen Körper, welche hörbare Töne hervorbringen, genau zu bestimmen, ist ziemlich schwierig, und die Physiker mussten deshalb vielerlei verhältnismäßig verwickelte Methoden einschlagen, um diese Aufgabe in jedem einzelnen Falle lösen zu können. Die mathematische Theorie und mannigfaltige Versuche mussten sich zu dem Ende gegenseitig zu Hilfe kommen. Zur Darlegung der Grundtatsachen in diesem Gebiete ist es deshalb sehr bequem, ein besonderes Toninstrument anwenden zu können, die sogenannte Sirene, welches durch seine Konstruktion es möglich macht, die Zahl der Luftschwingungen, die den Ton hervorgebracht haben, direkt zu bestimmen. Die einfachste Form der Sirene ist in Fig. 1 nach Seebeck in ihren Hauptteilen dargestellt.
A ist eine dünne Scheibe aus Pappe oder Blech, welche um ihre mittlere Achse b mittels der um ein größeres Rad laufenden Schnur ff schnell gedreht werden kann. Längs des Randes der Scheibe ist eine Reihe von Löchern in gleichen Abständen von einander angebracht, in der Zeichnung 12; eine oder mehrere andere Reihen gleichabstehender Löcher befinden sich auf anderen konzentrischen Kreislinien (in Fig. l eine solche von acht Löchern); c ist ein Röhrchen, welches gegen eines der Löcher gerichtet wird. Lässt man nun die Scheibe geschwind umlaufen, und bläst durch das Röhrchen c, so tritt die Luft frei aus, so oft eines der Löcher der Scheibe an der Mündung des Röhrchens vorbeigeht, während der Austritt der Luft gehindert ist, so oft ein undurchbohrter Teil der Scheibe vor der Mündung des Röhrchens steht. Jedes einzelne Loch der Scheibe, welches vor der Mündung der Röhre vorübergeht, lässt daher einen einzelnen Luftstoß austreten. Wird die Scheibe einmal umgedreht, und ist das Röhrchen gegen den äußeren Kreis gerichtet, so erhalten wir den 12 Löchern entsprechend 12 Luftstöße; ist das Röhrchen dagegen gegen den inneren Kreis gerichtet, nur 8 Luftstöße. Lassen wir die Scheibe in der Sekunde 10 mal umlaufen, so gibt uns der äußere Kreis angeblasen 120 Luftstöße in der Sekunde, welche als ein schwacher tiefer Ton erscheinen, und der innere Kreis 80 Luftstöße. überhaupt, wenn wir die Anzahl der Umläufe der Scheibe während einer Sekunde, und die Anzahl der Löcher der angeblasenen Reihe kennen, gibt uns offenbar das Produkt beider Zahlen die Zahl der Luftstöße. Diese. Zahl ist also hier viel leichter genau zu ermitteln als bei irgend einem anderen Tonwerkzeuge, und die Sirenen sind deshalb außerordentlich geeignet, um alle Veränderungen des Tons zu studieren, welche von den Veränderungen und den Verhältnissen der Schwingungszahlen abhängen.
Die hier beschriebene Form der Sirene gibt nur einen schwachen Ton; ich habe sie nur vorangestellt, weil die Art ihrer Wirkung am leichtesten zu verstehen ist, auch kann sie leicht, indem man die Scheibe wechselt, sehr verschiedenartigen Versuchen angepasst werden. Einen kräftigeren Ton gibt die in Fig. 2, 3 und 4 dargestellte Sirene nach Cagniard la Tour. SS ist die rotierende Scheibe, in Fig. 3 von oben gesehen, in Fig. 2 und 4 von der Seite. Sie befindet sich über einem Windkasten A, der durch das Rohr B mit einem Blasebalg verbunden werden kann. Der Deckel des Windkastens A, der unmittelbar unter der rotierenden Scheibe liegt, hat ebenso viele Durchbohrungen wie diese, und die Durchbohrungen im Deckel des Kastens und in der Scheibe sind so schräg gegen einander gerichtet, wie Fig. 4 zeigt (Fig. 4 ist ein Durchschnitt des Instruments in Richtung der Linie nn Fig. 3). Diese Stellung der Löcher bewirkt, daß der ausfahrende Wind die Scheibe SS selbst in Rotation versetzt, und man kann durch starkes Anblasen 50 bis 60 Rotationen in der Sekunde erzielen. Da sämtliche Löcher dieser Sirene gleichzeitig angeblasen werden, so erhält man einen viel stärkeren Ton als bei der Sirene von Seebeck. Zur Zählung der Umdrehungen dient das Zählerwerk zz, an dem sich ein gezahntes Rad befindet, welches in die Schraube t eingreift und bei jeder Umdrehung der Scheibe SS um einen Zahn vorwärts bewegt wird. Durch den Griff h kann man das Zählerwerk ein wenig verschieben, so daß es in die Schraube t nach Belieben eingreift oder nicht eingreift. Wenn man es bei einem Sekundenschlage einrückt, bei einem späteren ausrückt, zeigen die Zeiger an, wie viel Umläufe die Scheibe während der abgezählten Sekunden gemacht hat2).
Zunächst ist klar, daß, wenn die durchbohrte Scheibe einer dieser Sirenen mit gleichmäßiger Geschwindigkeit umläuft und die Luft stoßweise durch die Löcher ausströmt, die dadurch hervorgebrachte Bewegung der Luft periodisch ist in dem Sinne, wie wir dieses Wort gebraucht haben. Die Löcher haben gleiche Abstände von einander, sie folgen sich also bei der Umdrehung in gleichen Zeiträumen. Durch jedes Loch wird gleichsam ein Tropfen Luft in das äußere Luftmeer ausgeleert und erregt hier Wellen die ebenfalls in gleichen Zwischenzeiten sich folgen, gerade ebenso wie es regelmäßig fallende Tropfen auf einer Wasserfläche tun. Inner- halb jeder einzelnen Periode wird bei verschieden eingerichteten Sirenen jeder einzelne Luftstoß noch eine ziemlich verschiedene Form haben können, je nachdem die Löcher enger oder weiter, näher an einander oder entfernter sind, und je nachdem die Röhrenmündung gestaltet ist; aber jedenfalls werden sämtliche Luftstöße derselben Löcherreihe, so lange man die Geschwindigkeit der Drehung und die Stellung des Röhrchens unverändert lässt, eine regelmäßig periodische Luftbewegung geben und deshalb m Ohre die Empfindung eines musikalischen Klanges erregen müssen, was denn auch der Fall ist.
Es ergibt sich bei den Versuchen mit der Sirene zunächst leicht, daß zwei Löcherreihen von gleicher Anzahl der Löcher mit derselben Geschwindigkeit gedreht einen Klang von derselben Tonhöhe geben, wie auch immer die Größe und Form der Löcher oder des Röhrchens sein mag, ja daß wir denselben Ton sogar erhalten, wenn wir bei der Drehung der Scheibe einen Stift in die Löcher schlagen lassen, statt sie anzublasen. Daraus folgt also zunächst, daß die musikalische Höhe des Klanges nur abhängt von der Zahl der Luftstöße oder Schwingungen, nicht Von ihrer Form, Stärke oder Erregungsweise. Weiter ergibt sich mit diesem Instrumente sehr leicht, daß, wenn wir die Umdrehungsgeschwindigkeit der Scheibe steigern, womit natürlich auch die Anzahl der Luftstöße gesteigert wird, der Ton an Höhe zunimmt. Dasselbe geschieht, wenn wir bei unveränderter Umlaufsgeschwindigkeit erst eine Reihe Löcher von kleinerer Anzahl anblasen, dann eine von größerer. Die letztere gibt den höheren Ton.
Mit demselben Instrumente findet man nun auch sehr leicht die merkwürdige Beziehung, welche die Schwingungszahlen zweier Töne haben, die mit einander ein konsonierendes Intervall bilden. Man nehme eine Scheibe mit einer Reihe von 8, und einer von 16 Löchern, und blase sie gleichzeitig an, während die Umlaufsgeschwindigkeit der Scheibe konstant erhalten wird. Man wird zwei Töne hören, die genau im Verhältnis» einer Oktave zu einander stehen. Man steigere die Umlaufsgeschwindigkeit der Scheibe; beide Töne werden höher geworden sein, aber beide werden auch in der neuen Tonlage mit einander eine Oktave bilden. Daraus folgern wir, daß ein Ton, der die höhere Oktave eines anderen bildet, genau doppelt so viel Schwingungen, in gleicher Zeit macht, als der letztere.
Die oben in Fig. l abgebildete Scheibe hat zwei Reihen von 8 und 12 Löchern. Beide abwechselnd angeblasen geben zwei Töne, die eine genaue und reine Quinte mit einander bilden, welches auch die Umdrehungsgeschwindigkeit der Scheibe sein mag. Daraus folgt, daß zwei Töne im Verhältnis einer Quinte stehen, wenn der höhere drei Schwingungen macht, genau in derselben Zeit, wo der tiefere zwei macht.
Wenn ein Ton auf der Reihe von 8 Löchern angeblasen wird, brauchen wir 16 Löcher, um seine Oktave, 12 Löcher, um seine Quinte zu erhalten. Das Schwingungsverhältnis der Quinte zur Oktave ist also 12 : 16 oder 3:4, das Intervall zwischen Quinte und Oktave ist aber eine Quarte, und daraus ersehen wir, daß zwei Töne mit einander eine Quarte bilden, wenn der höhere vier Schwingungen in derselben Zeit ausführt, wo der tiefere drei macht.
Die mehrstimmige Sirene von Dove hat gewöhnlich vier Reihen von 8, 10, 12, 16 Löchern. Die Reihe von 16 Löchern gibt die Oktave der von 8, die Quarte der von 12 Löchern, die Reihe von 12 Löchern gibt die Quinte der von 8, die kleine Terz der von 10 Löchern, die letztere die große Terz der von 8 Löchern. Die vier Reihen geben also die Töne eines Dur-Akkords.
Durch diese und ähnliche Versuche ergeben sich folgende Verhältnisse der Schwingungszahlen:
So findet man durch verhältnismäßig einfache und leichte Versuche an der Sirene gleich das merkwürdige Gesetz, welches wir in der Einleitung erwähnt haben, bestätigt, wonach die Schwingungszahlen konsonanter Töne im Verhältnisse kleiner ganzer Zahlen stehen. Wir werden im Verlaufe unserer Untersuchung dasselbe Instrument wieder gebrauchen, um die Strenge und Genauigkeit dieses Gesetzes noch eingehender zu prüfen.
Längst, bevor man noch irgend etwas von Schwingungszahlen und deren Messung wusste, hatte Pythagoras gelehrt, daß man eine Saite durch einen Steg im Verhältnisse der genannten ganzen Zahlen teilen muß, wenn ihre beiden Abschnitte konsonante Töne geben sollen. Setzt man den Steg so, daß rechts 2/3 der Saite stehen bleiben, links 1/3, so stehen die beiden Längen im Verhältnisse 2:1 und geben das Intervall einer Oktave; das längere Saitenstück hat dabei den tieferen Ton. Setzt man den Steg so, daß rechts 3/5, links 2/5 der Länge liegen, so ist das Verhältnis der Stücke 3:2 und die Töne bilden eine Quinte.
Diese Abmessungen sind von den griechischen Musikern schon mit großer Genauigkeit ausgeführt worden, und sie hatten auf sie ein ziemlich künstliches Tonsystem gegründet. Zu diesen Messungen benutzte man ein besonderes Instrument, das Monochord, an welchem auf einem Resonanzkasten eine einzige Saite ausgespannt war; unter dieser befand sich ein Maßstab, um den Steg richtig setzen zu können.
Erst sehr viel später lernte man durch Galilei (1638), Newton, Euler (1729) und Daniel Bernouilli (1771) die Bewegungsgesetze der Saiten kennen, und ermittelte, daß die einfachen Verhältnisse der Saitenlängen auch ebenso für die Schwingungszahlen der Töne bestehen, und somit den Tonintervallen aller musikalischen Instrumente zukommen, und nicht allein denen der Saiten, an welchen man ursprünglich das Gesetz gefunden hatte.
Diese Beziehung der ganzen Zahlen zu den musikalischen Konsonanzen erschien von jeher als ein wunderbares und bedeutsames Geheimnis. Schon die Pythagoräer deuteten sie aus in ihren Spekulationen über die Harmonie der Sphären. Sie blieb von da ab teils das Ziel, teils der Ausgangspunkt der wunderlichsten und kühnsten phantastischen oder philosophischen Kombinationen, bis in neuerer Zeit die meisten Forscher sich der auch von Euler vertretenen Ansicht anschlossen, daß die menschliche Seele ein besonderes Wohlgefallen an einfachen Verhältnissen habe, weil sie diese leichter auffassen und übersehen könne. Aber es blieb unerörtert, wie es die Seele eines nicht in der Physik bewanderten Hörers, der sich vielleicht nicht einmal klar gemacht hat, daß Töne auf Schwingungen beruhen, anstelle, um die Verhältnisse der Schwingungszahlen zu erkennen und zu vergleichen. Nachzuweisen, welche Vorgänge im Ohre den Unterschied von Konsonanz und Dissonanz fühlbar machen, wird eine Hauptaufgabe der zweiten Abteilung dieses Buches sein.
Berechnung der Schwingungszahlen für sämtliche Töne der Tonleiter.
Mittels der angegebenen Verhältnisse für die konsonanten Intervalle lassen sich die Schwingungszahlen leicht für die ganze Ausdehnung der Tonleiter berechnen, indem wir der Reihe der konsonanten Intervalle durch die Tonleiter hin folgen.
Der Durdreiklang besteht aus der großen Terz und Quinte. Seine Verhältnisse sind:
G : D : E : F : G : A : H : C.
1 9/8 5/4 4 /3 3/2 5/3 15/8 2
Um die Rechnung auf andere Oktaven ausdehnen zu können, bemerken wir zunächst über die Bezeichnung der Töne Folgendes. Die deutschen Musiker bezeichnen die Töne der höheren Oktaven durch angehängte Striche wie folgt:
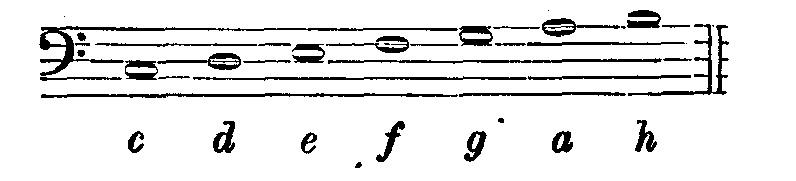
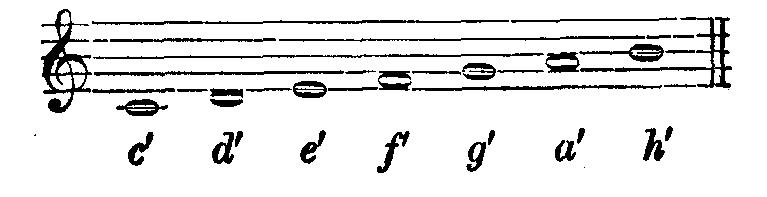
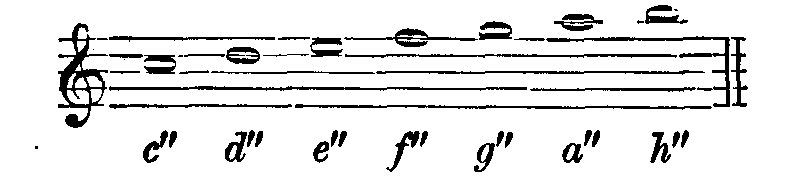
4. Große oder achtfüßige Oktave.
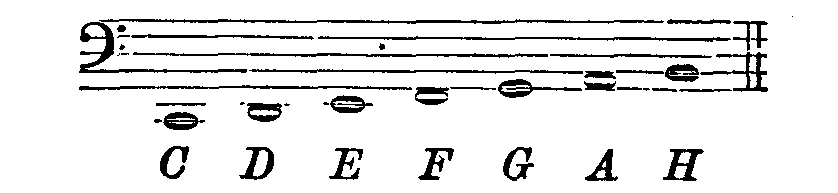
Da die Schwingungszahlen der nächst höheren Oktave stets doppelt so groß sind als die der tieferen, so findet man die Schwingungszahlen der höheren Töne, wenn man die der kleinen ungestrichenen Oktave so oft mit 2 multipliziert, als ihr Zeichen Striche oben bat, die der tieferen dagegen, wenn man die Schwingungszahlen der großen Oktave so oft mit 2 dividiert, als das Zeichen des Tons unten Striche hat.
3) Im Jahre 1859 hat die Pariser Akademie für denselben Ton 435 Schwingungen festgesetzt. In französischer Zählungsweise werden diese als 870 Schwingungen bezeichnet, da die französischen Physiker unzweckmäßiger Weise den Hin- und Hergang eines schwingenden Körpers als zwei Schwingungen bezeichnen, den Hingang als eine, den Hergang als die zweite. Diese Art zu zählen ist vom Sekundenpendel entnommen, welches beim Hingang einmal und beim Rückgang ein zweites Mal schlägt. Für symmetrisch hin- und hergehende Bewegungen wäre es gleichgültig, wie man zählt, aber bei den vielfältig vorkommenden asymmetrischen Bewegungen ist die französische Zählungsweise sehr hinderlich. Die Zahl 440 gibt weniger Brüche für die C-dur-Leiter, als das a' = 435. Der Unterschied der Stimmung ist weniger als ein Komma.
[Auf der internationalen Stimmtonkonferenz zu Wien im
Jahre 1885 wurden für den Normalstimmton 435 Schwingungen international
festgesetzt. (Anm. d. Her. 1895.)]
| Noten | Contra Oktave
C1 - H1 |
C - H |
Ungestrichene Oktave
c - h |
Eingestrichene Oktave
c' - h' |
Zweigestrichene Oktave
c" - h" |
Dreigestrichene Oktave
c'" - h"' |
Viergestrichene Oktave c"" - h'''' |
| C | 33 | 66 | 132 | 264 | 528 | 1056 | 2112 |
| D | 37,129 | 74,25 | 148,5 | 297 | 594 | 1188 | 2376 |
| E | 41,25 | 82,5 | 165 | 330 | 660 | 1320 | 2640 |
| F | 44 | 88 | 176 | 352 | 704 | 1408 | 2816 |
| G | 49,5 | 99 | 198 | 396 | 792 | 1584 | 3168 |
| A | 55 | 110 | 220 | 440 | 880 | 1760 | 3620 |
| H | 61,876 | 123,75 | 247,5 | 495 | 990 | 1980 | 3960 |
Der tiefste Ton der Orchesterinstrumente ist das E1 des Contrabasses mit 41 1/4 Schwingungen. Die neueren Klaviere und Orgeln gehen gewöhnlich bis zum C1 mit 33 Schwingungen, neuere Flügel auch wohl bis zum A11 mit 271/2 Schwingungen. Auf größeren Orgeln hat man auch noch eine tiefere Oktave bis zum C11 mit 16 1/2 Schwingungen, wie schon erwähnt ist. Aber der musikalische Charakter aller dieser Töne unterhalb des E1 ist unvollkommen, weil wir hier schon der Grenze nahe sind, wo die Fähigkeit des Ohrs, die Schwingungen zu einem Tone zu verbinden, aufhört. Wenn nicht die Auffassung der Tonhöhe unbestimmt werden soll, können diese tiefsten Töne deshalb auch nur mit ihren höheren Oktaven zusammen musikalisch gebraucht werden, wodurch die letzteren den Charakter größerer Tiefe bekommen.
Nach der Höhe gehen die Pianofortes meist bis zum aIV oder auch cv von 3520 und 4224 Schwingungen, der höchste Ton des Orchesters möchte das 5 gestrichene d von 4752 Schwingungen auf der Piccoloflöte sein. Appun und W. Preyer haben durch kleine Stimmgabeln, die mit dem Violinbogen gestrichen wurden, neuerdings das 8 gestrichene e von 40960 Schwingungen erreicht und gehört. Diese hohen Töne waren sehr schmerzhaft unangenehm, und die Unterscheidung der Tonhöhe ist bei denen, die über die Grenze der musikalischen Skala hinausliegen, sehr unvollkommen. Mehr darüber im neunten Abschnitt.
Die musikalisch gut brauchbaren Töne mit deutlich wahrnehmbarer Tonhöhe liegen also zwischen 40 und 4000 Schwingungen, im Bereiche von 7 Oktaven, die überhaupt wahrnehmbaren zwischen etwa 20 und 40000, im Bereiche von etwa 11 Oktaven. Man sieht hieraus, ein wie großer Umfang von verschiedenen Werten der Schwingungszahlen vom Ohre wahrgenommen und unterschieden werden kann. Hierin ist das Ohr dem Auge, welches Licht von verschiedener Schwingungsdauer ebenfalls als verschiedenartig unterscheidet, außerordentlich überlegen, denn der Umfang der vom Auge wahrnehmbaren Lichtschwingungen geht wenig über eine Oktave.
Stärke und Tonhöhe waren die ersten beiden Unterschiede, welche wir zwischen verschiedenen Klängen fanden, der dritte war die Klangfarbe, zu deren Untersuchung wir nun zu schreiten haben. Wenn man nach einander dieselbe Note von einem Klaviere, einer Violine, einer Klarinette, Oboe, Trompete und einer menschlichen Stimme angegeben hört, so ist trotz gleicher Stärke und gleicher Tonhöhe der Klang aller dieser Instrumente verschieden, und wir erkennen an dem Klange mit der größten Leichtigkeit das Instrument wieder, welches ihn hervorgebracht hat Die Abänderungen der Klangfarbe erscheinen unendlich mannigfaltig, denn abgesehen davon, daß wir noch eine lange Reihe von verschiedenen musikalischen Instrumenten haben, die alle dieselbe Note würden hervorbringen können, abgesehen davon, daß die verschiedenen Exemplare desselben Instruments und die Stimmen verschiedener menschlicher Individuen noch gewisse feinere Abänderungen der Klangfarbe zeigen, die unser Ohr unterscheidet, kann dieselbe Note zuweilen selbst auf demselben Instrumente noch mit mancherlei Abänderungen der Klangfarbe hervorgebracht werden. Unter den musikalischen Instrumenten sind in dieser Beziehung namentlich die Streichinstrumente ausgezeichnet. Noch reicher ist die menschliche Stimme, und die menschliche Sprache benutzt eben diese Abänderungen der Klangfarbe, um die verschiedenen Buchstaben zu charakterisieren. Als anhaltende, musikalisch verwendbare Klänge der Stimme sind hier namentlich die verschiedenen Vokale zu nennen, während die Bildung der Konsonanten meistens auf kurz vorübergehenden Geräuschen beruht.
Wenn wir nun fragen, welcher äußeren physikalischen Verschiedenheit der Schallwellen die verschiedenen Klangfarben entsprechen, so haben wir gesehen, daß die Weite der Schwingung der Stärke, die Dauer der Schwingung der Tonhöhe entspricht. Von beiden kann die Klangfarbe nicht abhängig sein. Dann bleibt keine andere Möglichkeit übrig, als daß die Klangfarbe abhänge von der Art und Weise, wie die Bewegung innerhalb jeder einzelnen Schwingungsperiode vor sich geht. Wir haben zur Erzeugung eines musikalischen Klanges von der Bewegung des tönenden Körpers nur gefordert, daß sie periodisch sei, das heißt, daß innerhalb jeder Schwingungsperiode genau dasselbe geschehe, was in den vorausgegangenen Perioden eben geschehen ist. Welche Art von Bewegung innerhalb jeder einzelnen Periode vor sich geht, war ganz beliebig geblieben, so daß in dieser Beziehung noch eine unendliche Mannigfaltigkeit der Schaubewegung möglich bleibt.
Betrachten wir Beispiele, und zwar zuerst solcher periodischer Bewegungen, die langsam genug gehen, daß wir ihnen mit dem Auge folgen können. Nehmen wir zuerst ein Pendel, wie wir es uns jederzeit verfertigen können, indem wir einen schweren Körper an einem Faden aufhängen und in Bewegung setzen. Das Pendel schwankt von rechts nach links in gleichmäßiger, nirgends stoßweise unterbrochener Bewegung, nahe den beiden Enden seiner Bahn bewegt es sich langsam, in der Mitte schnell. Unter den tönenden Körpern, welche in derselben Weise sich bewegen, nur viel schneller, wären die Stimmgabeln zu nennen. Wenn man eine Stimmgabel entweder angeschlagen oder durch Streichen mit dem Violinbogen erregt hat, und sie nun langsam austönen lässt, bewegen sich ihre Zinken genau in derselben Weise und nach demselben Gesetze hin und her, wie ein Pendel, nur daß sie viele hundert Schwingungen in derselben Zeit vollführen, wo letzteres eine macht.
Ein anderes Beispiel einer periodischen Bewegung wäre ein Hammer, der von einer Wassermühle bewegt wird. Er wird langsam von dem Mühlwerk gehoben, dann losgelassen und fallt plötzlich herunter, wird dann wieder langsam gehoben, und so fort. Hier haben wir es wieder mit einem periodischen Hin- und Hergang zu tun, aber es ist ersichtlich, daß die Art dieser Bewegung eine ganz andere ist als die des Pendels. Unter den tönenden Bewegungen würde diesem Falle ziemlich nahe entsprechen die Bewegung einer Violinsaite, die vom Bogen gestrichen wird, wie wir es im fünften Abschnitt genauer beschreiben werden. Die Saite haftet eine Zeit lang am Bogen fest, wird von diesem mitgenommen, bis sie sich plötzlich losreißt, wie der Hammer in der Mühle, und nun wie dieser mit viel größerer Geschwindigkeit, als sie gekommen ist, ein Stück zurückspringt, wo sie dann von Neuem durch den Bogen gefasst und mitgenommen wird.
Man denke ferner an einen Ball, der, senkrecht in die Höhe geworfen, beim Herabfallen von dem Ballschläger mit einem Schlag empfangen wird, so daß er wieder ebenso hoch hinaufsteigt als vorher, was sich dann immer in gleichen Zeitabschnitten wiederholen mag. Ein solcher Ball würde zum Aufsteigen so viel Zeit brauchen wie zum Absteigen, seine Bewegung würde am tiefsten Punkte seiner Bahn ruckweise unterbrochen, oben aber von immer langsamerem Aufsteigen in allmählig zunehmendes Absteigen übergehen. Dies wäre also eine dritte Art einer hin- und hergehenden periodischen Bewegung, deren Verlauf sich aber von den beiden früheren wesentlich unterscheidet.
Um das Gesetz solcher Bewegungen dem Auge übersichtlicher darzulegen, als es durch weitläufige Beschreibungen geschehen kann, pflegen die Mathematiker und Physiker eine graphische Methode anzuwenden, die auch wir noch oft zu benutzen gezwungen sein werden, und deren Sinn ich deshalb hier auseinandersetzen muss.
Um diese Methode verständlich zu machen, wollen wir voraussetzen, daß an der Gabel A, Fig. 5, ein Stiftchen b befestigt sei, welches auf der Papierfläche B B zeichnen könne. Es möge entweder die Gabel mit gleichförmiger Geschwindigkeit in Richtung des oberes Pfeils über das Papier hingeschoben werden, oder das Papier in entgegengesetzter Richtung, nämlich in Richtung des unteren Pfeils, unter ihr fortgezogen werden, so daß die Gabel, wenn sie bei dieser Bewegung nicht tönend ist, gerade die punktierte Linie dc aufschreibt. Wird nun aber die Gabel über das Papier in derselben Weise hingeführt, während ihre Zinken dabei in Schwingung versetzt sind, so wird sie die Wellenlinie cd auf das Papier schreiben. Wenn sie nämlich schwingt, wird das Ende ihrer Zinke mit dem Stiftchen b fortdauernd hin- und hergehen, und sich bald über, bald unter der punktierten Linie cd befinden, wie es die aufgezeichnete Wellenlinie anzeigt. Diese Linie, nachdem sie auf das Papier gezeichnet ist, bleibt stehen als ein Bild von derjenigen Art der Bewegung, welche das Ende der Gabel während der tönenden Schwingungen ausgeführt hat. Da nämlich das Stiftchen b in Richtung der Geraden cd mit konstanter Geschwindigkeit sich verschoben hat, so entsprechen gleiche Abschnitte der Linie cd gleichen kleinen Zeitabschnitten dieser Bewegung, und die Entfernung der Wellenlinie nach oben oder unten von der betreffenden Stelle der Linie cd zeigt an, um wieviel in den betreffenden Zeitabschnitten das Stiftchen b nach oben oder unten aus seiner Gleichgewichtslage abgewichen war.
Wenn ein solcher Versuch, wie er hier angedeutet ist, wirklich ausgeführt werden soll, so tut man am besten, das Papier über einen Zylinder zu ziehen, der durch ein Uhrwerk in gleichförmige Rotation versetzt wird. Nachdem das Papier angefeuchtet ist, lässt man es über einer Terpentinölflamme umlaufen, so daß es sich mit Ruß bezieht; dann kann man mit einem feinen, etwas abgerundeten Stahlspitzchen leicht feine Striche darauf ziehen. Fig. 6 ist die Kopie einer Zeichnung, die in dieser Weise von einer Stimmgabel auf dem rotierenden Zylinder des Phonautographen der Herren Scott und König ausgeführt ist.
Die Fig. 7 stellt einen Teil derselben Kurve in vergrößertem Maßstabe dar. Die Bedeutung einer solchen Kurve ist leicht einzusehen. Der Zeichenstift ist in Richtung der Linie eh mit gleichmäßiger Geschwindigkeit fortgeglitten. Nehmen wir an, er habe für das Stück eg 1/10 Sekunde gebraucht, teilen wir eg in 12 gleiche Teile, wie es in der Zeichnung geschehen ist, so wird der Zeichenstift, um die Breite eines solchen Teiles in horizontaler Richtung zurückzulegen, die Zeit von 1/120 Sekunde gebraucht haben, und die Kurve zeigt uns an, auf welcher Seite und wie weit entfernt von der Ruhelage der schwingende Stift nach 1/120, 2/120 u. s. w. Sekunde, oder überhaupt nach jeder beliebigen kurzen Zeitdauer von dem Augenblicke an gerechnet sich befand, wo er durch den Punkt e ging. Wir sehen, daß er nach 1/120 Sekunde um die Höhe l nach oben abgewichen war, daß seine Abweichung zunahm bis 3/120 Sekunde, dann wieder abnahm, daß er nach 6/120 = 1/20 Sekunde wieder in seiner Gleichgewichtslage war, dann nach der entgegengesetzten Seite abwich u. s. w. Und wir können auch weiter leicht bestimmen, wo der schwingende Stift nach einem beliebigen Bruchteile dieser Hundertzwanzigteile einer Sekunde sich befand. Eine solche Zeichnung zeigt also unmittelbar, an welcher Stelle seiner Bahn sich der schwingende Körper in jedem beliebig gewählten Zeitmoment befand, und gibt somit ein vollständiges Bild seiner Bewegung. Will der Leser die Bewegung des schwingenden Punktes sich reproduzieren, so schneide er sich in ein Blatt Papier einen senkrechten schmalen Schlitz, lege das Papier über Fig. 6 oder 7, so daß er durch den senkrechten Schlitz einen kleinen Teil der Kurve sieht, und ziehe nun das Buch unter dem Papier langsam fort, so wird der weiße oder schwarze Punkt in dem Schlitz gerade so hin- und hergehen, nur langsamer, als es ursprünglich die Gabel getan hat.
Nun können wir nicht alle schwingenden Körper ihre Schwingungen direkt auf Papier schreiben lassen, obgleich in den hierzu dienenden Methoden neuerdings manche Fortschritte gemacht sind. Aber wir können doch für alle tönenden Körper solche Kurven zeichnen, welche graphisch in derselben Weise ihre Bewegung darstellen, wenn wir das Gesetz dieser Bewegung kennen, das heißt, wenn wir wissen, wie weit von seiner Gleichgewichtslage der schwingende Punkt in jedem beliebig gewählten Zeitpunkte gewesen ist Denn tragen wir auf einer Horizontallinie wie ef, Fig. 7, Längen auf, welche die Zeitdauer darstellen, und senkrecht dazu nach oben oder nach unten hin Lothe, welche der Entfernung des schwingenden Punktes von seiner Mittellage gleich oder proportional sind: so erhalten wir, indem wir die Enden der Lothe verbinden, eine Kurve, wie sie der schwingende Körper gezeichnet haben würde, wenn es möglich gewesen wäre, ihn zeichnen zu lassen.
So stellt Fig. 8 die Bewegung des vom Wasserrade gehobenen Hammers oder des vom Violinbogen angegriffenen Punktes der Saite dar, während der ersten neun Zeitteile steigt er langsam und gleichmäßig empor, während des zehnten springt er plötzlich herab.
Fig. 9 stellt die Bewegung des Balles dar, der, wenn er unten angekommen ist, wieder in die Höhe geschlagen wird. Aufsteigen und Absteigen geschieht gleich schnell, während in Fig. 8 ersteres langsamer vor sich geht. Nur am tiefsten Funkte der Bahn wird die Bewegung durch den Schlag plötzlich geändert.
Indem die Physiker diese Kurvenformen im Sinne haben, welche das Gesetz der Bewegung des tönenden Körpers darstellen, sprechen sie denn auch geradezu von der Schwingungsform eines tönenden Körpers, und behaupten, daß von dieser Schwingungsform die Klangfarbe abhänge. Diese Behauptung, welche sich bisher nur darauf gründete, daß man wusste, die Klangfarbe könne nicht von der Schwingungsdauer und nicht von der Schwingungsbreite oder Stärke abhängen, werden wir in der Folge einer näheren Prüfung unterwerfen. Sie wird sich in so weit als richtig erweisen, daß jede verschiedene Klangform eine verschiedene Schwingungsform verlangt, dagegen verschiedene Schwingungsformen gleicher Klangfarbe entsprechen können.
Wenn wir die Einwirkung verschiedener Wellenformen, z. B. der in Fig. 8 gezeichneten, die etwa der Violinsaite entspricht, auf das Ohr genau und aufmerksam untersuchen, so ergibt sich eine sonderbare und unerwartete Tatsache, welche zwar lange genug einzelnen Musikern und Physikern bekannt gewesen ist, aber meistens nur als ein Kuriosum betrachtet wurde, da man ihre Allgemeinheit und ihre große Bedeutung für alle Klangerscheinungen nicht kannte. Das Ohr, von solchen Schwingungen getroffen, hört nämlich bei gehörig angestrengter Aufmerksamkeit nicht nur denjenigen Ton, dessen Tonhöhe durch die Dauer der Schwingungen in der Weise bestimmt ist, wie wir dies vorher auseinandergesetzt haben, sondern es hört außer diesem noch eine ganze Reihe höherer Töne, welche wir die harmonischen Obertöne des Klanges nennen, im Gegensatze zu jenem ersten Tone, dem Grundtone, der unter ihnen allen der tiefste und in der Regel auch der stärkste ist, und nach dessen Tonhöhe wir die Tonhöhe des ganzen Klanges beurteilen. Die Reihe dieser Obertöne ist für alle musikalischen Klänge, die einer regelmäßig periodischen Luftbewegung entsprechen, genau dieselbe; es sind nämlich folgende:
1. Die höhere Oktave des Grundtons, welche doppelt so viel Schwingungen
macht, als der Grundton. Nennen wir den Grundton c, so ist diese höhere
Oktave c' ;
2. die Quinte dieser Oktave g macht 3 mal so viel Schwingungen
als der Grundton;
3. die zweite höhere Oktave c" macht 4 mal so viel
Schwingungen;
4. die große Terz dieser Oktave e" mit 5 mal so
viel Schwingungen;
5. die Quinte dieser Oktave g" mit 6 mal so viel Schwingungen.
Daran schließen sich immer schwächer und schwächer werdend die Töne, welche 7-, 8-, 9mal u. s. w. so viel Schwingungen als der
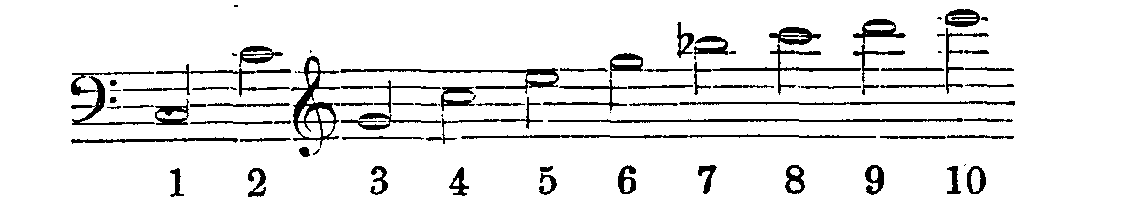
Wir haben die Gesamtempfindung, welche eine periodische Lufterschütterung im Ohre hervorbringt, Klang genannt. Jetzt finden wir eine Reihe verschiedenartiger Töne in ihm enthalten, die wir die Teiltöne oder Partialtöne des Klanges nennen wollen. Der erste dieser Teiltöne ist der Grundton des Klanges, die übrigen seine harmonischen Obertöne. Die Ordnungszahl jedes Partialtons gibt an, wie viel Mal größer seine Schwingungszahl ist, als die des Grundtons. Es macht also der zweite Teilton zwei Mal so viel Schwingungen, der dritte drei Mal so viel Schwingungen als der Grundton u. s. w.
Es ist zuerst von G. S. Ohm ausgesprochen und behauptet worden, daß es nur eine einzige Schwingungsform gibt, deren Klang keine harmonischen Obertöne enthält, deren einziger Bestandteil also der Grundton ist. Es ist dies die Schwingungsform, welche wir oben als dem Pendel und den Stimmgabeln eigentümlich beschrieben und in Fig. 6 und 7 abgebildet haben. Wir wollen sie die pendelartigen Schwingungen nennen, oder, da ihr Klang keine weitere Zusammensetzung aus verschiedenen Tönen hören lässt, die einfachen Schwingungen. In welchem Sinne nicht bloß alle anderen Klänge, sondern auch alle anderen Schwingungsformen als zusammengesetzt betrachtet werden können, wird sich später zeigen. Die Bezeichnung einfache oder pendelartige Schwingung4) werden wir also als gleichbedeutend gebrauchen. Wir beschränken ferner den Gebrauch des Wortes Ton durchaus auf den Klang einfacher Schwingungen, während bisher Ton meist in derselben Bedeutung wie Klang gebraucht worden ist. Aber es ist durchaus nötig, in der Akustik zwischen dem Klange, d. h. dem Eindruck einer periodischen Luftbewegung überhaupt, und dem Tone, dem Eindruck einer einfachen Schwingung, zu unterscheiden, und der bisherige Sprachgebrauch scheint mir diese Feststellung der Begriffe zu rechtfertigen. Wir sprechen von Tonhöhe, welche nur einem einzelnen Tone zukommen kann, während einem Klange streng genommen verschiedene Tonhöhen zuzuschreiben sind, seinen verschiedenen Teiltönen entsprechend. und wir sprechen von einem Zusammenklange verschiedener Instrumente, wo das Wort Ton entschieden nicht mehr angewendet werden kann. Die hier besprochenen Tatsachen lehren, daß jeder Klang, welcher Obertöne unterscheiden lässt, wirklich schon ein Zusammenklang verschiedener Töne ist.
Da nun die Klangfarbe, wie wir gesehen haben, von der Schwingungsform abhängt, von derselben Schwingungsform aber auch das Vorkommen der Obertöne bestimmt wird, so werden wir die Frage aufwerfen müssen, in wie fern die Unterschiede der Klangfarbe etwa auf verschiedenartigen Verbindungen des Grundtons mit verschieden starken Obertönen beruhen. Es bietet sich uns durch diese Fragestellung ein Weg dar, um den Grund des bisher vollkommen rätselhaften Wesens der Klangfarbe aufhellen zu können. Dann aber müssen wir auch notwendig die Frage zu lösen versuchen, wie denn das Ohr dazu komme, jeden Klang in eine Reihe von Teiltönen zu zerlegen, und welchen Sinn diese Zerlegung habe. Dies wird das Geschäft der nächsten Abschnitte sein.
4) Das Gesetz dieser Schwingung lässt sich populär mittels der in Fig. 10 dargestellten Konstruktion auseinandersetzen. Man denke sich einen Punkt in der um c beschriebenen Kreislinie mit gleichförmiger Geschwindigkeit umlaufend, und einen Beobachter in großer Entfernung in die Verlängerung der Linie eh gestellt, so daß er nicht die Fläche des besagten Kreises sieht, sondern nur die Kante dieser Fläche, so wird diesem der in der Kreislinie umlaufende Punkt so erscheinen, als ob er nur längs des Durchmessers a b auf- und abstiege. Dieses Auf- und Absteigen würde aber genau nach dem Gesetze der pendelartigen Schwingungen geschehen. — um diese Bewegung durch eine Kurve graphisch darzustellen, teile man die Länge eg, welche der Zeitdauer einer ganzen Schwingung entsprechen möge, in ebenso viele (hier 12) gleiche Teile als die Peripherie des Kreises, und mache die Lothe l, 2, 3 u. s. w. auf den Teilpunkten der Linie eg der Reihe nach gleich denen, die in dem Kreise von den entsprechenden Teilpunkten l, 2, 8 u. s. w. gefällt sind. So erhält man die in Fig. 10 gezeichnete Kurve, welche mit der von der Stimmgabel gezeichneten, Fig. 6, der Form nach übereinstimmt, nur größere Dimensionen hat.
Mathematisch ausgedrückt ist bei der einfachen Schwingung die Entfernung des schwingenden Punktes von der Gleichgewichtslage gleich dem Sinus eines der Zeit proportional wachsenden Bogens, daher die einfachen Schwingungen auch Sinusschwingungen genannt werden.