Das mechanische Problem, auf dessen Lösung es hier ankommt, ist zu untersuchen, ob eine zusammenhängende Membran von ähnlichen Eigenschaften, wie die Membrana basilaris der Schnecke, so schwingen kann, wie es Herr Hensen für letztere vorausgesetzt hat; so nämlich, daß jedes Faserbündel der Membran auf einen seiner Länge und Spannung entsprechenden Ton mitschwinge, ohne daß die benachbarten Fasern merklich in Bewegung gesetzt würden. Wir können bei dieser Untersuchung abstrahieren von der spiraligen Krümmung der Basilarmembran der Schnecke, und uns dieselbe gerade ausgespannt denken zwischen den Schenkeln eines Winkels, dessen Größe wir mit 2h bezeichnen. Die Halbierungslinie desselben möge die Achse der x sein, und rechtwinklig dagegen die Achse der y durch den Scheitel des Winkels gelegt sein. Die Spannung der Membran parallel der x-Achse möge gleich P, dagegen parallel der y-Achse gleich Q sein, beide gemessen durch die Kräfte, welche auf die der Längeneinheit gleichen, den x und y beziehlich parallelen Seiten eines Quadrats ausgeübt werden müssen, um der Spannung der Membran das Gleichgewicht zu halten. Die Masse eines solchen Quadrats sei m , ferner t die Zeit und z die Ausweichung eines Membranpunktes von der Gleichgewichtslage desselben. Ferner sei Z eine äußere Kraft, welche in Richtung der positiven z auf die Membran wirkt, und diese in Schwingung versetzt. Die Bewegungsgleichung der Membran, wie sie aus dem Hamilton'schen Prinzipe nach dem Vorgänge von Kirchhoff ohne prinzipielle Schwierigkeit entwickelt werden kann, ist alsdann:

......................................................(1)

l) daß z gleich Null sei längs der Schenkel des Winkels, also wo

3) daß z endlich sei für unendlich große Werte von x.

In welcher Weise statt dieser beiden letzteren Grenzbedingungen, welche für unseren Zweck genügen, auch gewisse bestimmte Kurven als feste Grenzen zwischen den Schenkeln des Winkels 2heingeführt werden können, wird die weitere Entwickelung lehren.

Die Gleichung (l) kann auf eine bekanntere Form gebracht werden, wenn wir setzen:

und . Wir erhalten dann .....................................................(1a)

Die Grenzbedingungen werden bei dieser Bezeichnung;

l) daß z = 0 für

3) daß z endlich sei für x = ¥ .

Die transformierte Aufgabe unterscheidet sich also von der ursprünglichen nur dadurch, daß die transformierte Membran gleichmäßig gespannt, und in einem Winkel von anderer Größe (die wir mit 2e bezeichnen wollen) ausgespannt ist.

Da bei der von uns beabsichtigten Anwendung P sehr klein gegen Q genommen werden wird, so wird auch dieser Winkel e , den die transformierte Membran ausfüllt, sehr klein, ein Umstand, in welchem wesentlich die analytischen Schwierigkeiten der Aufgabe begründet sind.

Nach diesen Vorbemerkungen führen wir zur analytischen Behandlung der Gleichungen (l) oder (la) Polarkoordinaten ein, indem wir setzen

...........................................................(1b)

........................................(1c) Die Grenzbedingungen sind, daß

,

3) z endlich, wenn r unendlich.

Was die Natur der Kraft Z anbetrifft, so nehmen wir an, daß sie einen Teil habe, der von der Reibung herrührt, und den wir gleich  setzen dürfen, worin v eine positive reelle Konstante bezeichnet.

Zweitens, daß das umgebende Medium einen periodisch veränderlichen Druck auf die Membran ausübe, und zwar gleichmäßig über die ganze Fläche der Membran. Somit setzen wir

.........(2)

...............................................................(2a)

,

...........................(2b)

Nachdem auf diese Weise die Variable t aus der Differentialgleichung beseitigt ist, kann dasselbe auch mit Berücksichtigung der ersten Grenzbedingung für w geschehen, indem wir z sowohl, wie die Konstante A, in eine nach Cosinus der ungeraden Vielfachen des Winkels  fortschreitende Reihe verwandeln. Bekanntlich ist innerhalb der Grenzen  und - 

etc ..........................(3) Setzen wir dem entsprechend etc ..........................(3a)

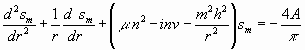.............................(3b)

1) s_m = 0 für r = 0,

2) s_m, endlich für r = ¥.

Daß jedes s_m durch diese Bedingungen vollständig bestimmt ist, zeigt sich leicht. Denn gäbe es zwei verschiedene Funktionen, welche der Gleichung (3b) und den beiden Grenzbedingungen genügten, so würde ihre Differenz, die wir mit s bezeichnen wollen, den Bedingungen genügen

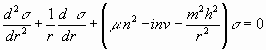....................................(3c)

1) s = 0 für r = 0,

2) s endlich sein für r = ¥ .

Beides zusammen ist nicht möglich für Bessel'sche Funktionen, bei denen das v einen noch so wenig von Null verschiedenen Wert hat. Nur wenn v = 0 ist, d. h. gar keine Reibung besteht, ist die gegebene Bestimmung ungenügend. Dann können nämlich einmal eingeleitete Oszillationen unendliche Zeit fortbestehen, auch wenn keine Kraft da ist, die ihnen neue Anstöße gibt.

Partikuläre Integrale der Gleichung (3b) lassen sich in Form von Reihen leicht entwickeln, ähnlich wie die Reihen für die verwandten Bessel'schen Funktionen, welche der Gleichung (3c) genügen. Die eine dieser Reihen läuft nach ganzen Potenzen von r fort, und ist immer konvergent. Aber wenn der Winkel e sehr klein ist, wird die Zahl der Glieder dieser Reihe, die zur Bestimmung des Wertes von s nötig ist, sehr groß, und die Reibe selbst deshalb unbrauchbar zur Diskussion des Ganges der Funktion. — Eine zweite Keine, die nach negativen Potenzen von r fortläuft, und ein anderes partikuläres Integral gibt, ist semikonvergent, und nur wenn h eine gerade ganze Zahl ist, eine algebraische Funktion. Im letzteren Falle wird dagegen die erstgenannte Reihe in ihren einzelnen Gliedern unendlich.

Für den vorliegenden Zweck ist es daher zweckmäßiger, den gesuchten Ausdruck für s in Form von bestimmten Integralen zu bilden.

Man bezeichne mit j und y folgende beiden Integrale:

_}.................................................(4)

.............................................................................(4a)

.....................................(4b)

Daß der in (4b) gegebene Ausdruck die Gleichung (3b) erfüllt, ergibt sich, wenn man ersteren in letztere substituiert, und bei der Differentiation unter den Integralzeichen von y und j darauf achtet, durch partielle Integration die unter dem Integralzeichen auftretenden Faktoren cos t, beziehlich fortzuschaffen.

Für r = 0 wird

also s_m = 0.

Mittels der Gleichung (4b) können wir nun untersuchen, wie der Wert von s_m ausfällt, wenn P, die Spannung der Membran in Richtung der x, verschwindend klein wird. Es wird dann, wie aus den Gleichungen (1b) folgt, r unendlich groß; ebenso h, dessen Wert ist

. Setzen wir aber r = h r

.

...............................................(5)

In dem Integrale y dagegen

Man kann deshalb für ein unendlich großes h den obigen Ausdruck für y ersetzen durch folgenden:

..........................................................(5a)

................................................(5b)

,

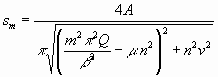.......................................(5d)

Für eine Saite übrigens ergibt sich derselbe Ausdruck, wenn man von Anfang an in Gleichung (l) z nur als Funktion von y in einer Linie betrachtet, und als unabhängig von x ansieht, als Grenzbedingung aber festhält, daß für y = ±b die Gleichung z = 0 stattfinde. Die Bewegung der Membran ist also dieselbe, als wenn sie aus einer Reihe neben einander liegender unverbundener Saiten bestände.

Der Wert von s_m in (5d) gibt uns die Amplitude der betreffenden Schwingungsform mit der Schwingungszahl  und mit m schwingenden Querabteilungen der Membran. Das Maximum von s_m wird eintreten, wo

..................................................(6)

Wenn wir den Wert von b, welcher die Gleichung (6) erfüllt, mit b bezeichnen, so können wir Gleichung (5d) schreiben

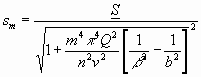
Je größer der Reibungskoeffizient v ist, desto mehr werden sich im Allgemeinen die Schwingungen jedes Tons auf der Membran ausbreiten.

Die hier ausgeführte mathematische Analyse zeigt an, daß jeder zugeleitete Ton auch alle diejenigen Querfaserzüge der Membran erregen muß, auf denen er als Eigenton mit Bildung von Knotenpunkten erscheinen kann. Daraus würde folgen, daß wenn die Membran des Labyrinths von durchaus gleichmäßiger Struktur wäre, wie die hier vorausgesetzte Membran, jede Erregung eines Querfaserbündels durch den betreffenden Grundton auch begleitet sein müßte von schwächeren Erregungen der ungeraden harmonischen Untertöne, deren Intensität allerdings mit den Faktoren ,, allgemein  multipliziert sein würde. Diese Hypothese ist von Herrn Dr. Hugo Riemann in seiner "Musikalischen Logik" aufgestellt worden, doch ist davon im Öhre nichts zu bemerken. Ich glaube aber, daß man dies nicht notwendig als einen Einwand gegen die hier durchgeführte Theorie betrachten darf, da wahrscheinlich durch die Anhangsgebilde der Membrana basilaris die Bildung von Tönen mit Knotenlinien sehr erschwert ist.

Man kann die Lösung auch ohne Schwierigkeit ausdehnen auf den Fall, wo die Membran im Felde der x , v durch zwei Kreisbögen begrenzt ist, deren Mittelpunkt im Scheitel des Winkelst liegt. Dem entsprechen dann in Wirklichkeit, also im Felde der x, y, zwei elliptische Begrenzungsbögen, die, wenn P verschwindet, zu geraden Linien werden. Man hat dem Werte von sm in (4b) nur noch ein vollständiges Integral der Gleichung (3c) hinzuzufügen, welches durch Bessel'sche Funktionen mit zwei willkürlichen Konstanten darzustellen, ist. Letztere sind so zu bestimmen, daß s_m an den gewählten Grenzkurven gleich Null wird. Wenn v klein ist, hat diese Änderung der Grenzen keinen wesentlichen Einfluß auf die Bewegung der Membran, außer wenn dies Maximum der Schwingung in die Nähe der Grenze fällt.