Zur Theorie der Pfeifen.
A. Einfluß der Resonanz in den Zungenpfeifen.
Zu Seite 166.
Die Resonanz ist für die einzelnen Glieder getrennt zu bestimmen,
da die den einzelnen Obertönen entsprechenden Schwingungsbewegungen
sich ungestört einander superponieren. Wenn wir nun unter l
die Länge der Röhre, unter Q ihren Querschnitt, unter
l + a die reduzierte Länge der Röhre (die Differenz
a
ist bei zylindrischen Röhren gleich dem Radius, multipliziert mit ![]() ,
unter
k die Größe
,
unter
k die Größe ![]() (l
die Wellenlänge) verstehen, und wenn wir das Potential der Wellen
im freien Raume für den Ton von der Schwingungszahl an gleich
(l
die Wellenlänge) verstehen, und wenn wir das Potential der Wellen
im freien Raume für den Ton von der Schwingungszahl an gleich
Für anders geformte Hohlkörper mit engen Mündungen lassen sich ähnliche Gleichungen mittels der in §. 10 derselben Abhandlung aufgestellten Sätze gewinnen.
Da die Bedingung starker Resonanz ist, daß cos ak (l + a) = 0 sei, so werden gleichzeitig mit dem Grundtone in zylindrischen Röhren (Klarinette) nur die ungeraden Obertöne verstärkt werden.
Im Innern von kegelförmigen Röhren können wir das Potential der Luftbewegung für den Ton n setzen gleich
![]()
ka == — tang (kl).
k (a + l) = a p
Unter übrigens gleichen Umständen wird die Anzahl und Größe der Glieder der Reihe 1, welche die erregende Luftbewegung darstellt, desto größer sein, je vollständiger der eintretende Luftstrom unterbrochen wird. Durchschlagende Zungen müssen deshalb ihrem Rahmen sehr eng anschließen, um einen kräftigen Ton zu geben. Aufschlagende Zungen dagegen, welche vollständigeren Verschluß zu Stande bringen, sind in dieser Beziehung überlegen. Nach den von Herrn A. E1lis2) eingezogenen Informationen haben in der Tat die Orgelbauer sich neuerdings wieder mehr der Anwendung aufschlagender Zungen zugeneigt. Die Zungen werden aber ganz schwach gekrümmt, so daß sie nicht mit einem Male gegen den Rahmen schlagen, sondern sich allmählich an diesem abrollen.
2) In der englischen Übersetzung dieses Werks. App.
XIX, H. 7, S. 711.
B. Theorie des Anblasens der Pfeifen.
Wenn in der Luftmasse einer Röhre erst einmal longitudinale Wellen erregt sind, so können diese viele Male zwischen beiden Enden hin und her reflektiert werden und periodisch wiederkehrende stehende Schwingungen bilden, ehe sie erlöschen. Am geschlossenen Ende einer gedackten Pfeife wird die Reflexion jedes Wellenzuges eine ziemlich vollständige sein müssen, an den offenen Enden jedoch geht immer ein merklicher Bruchteil der Welle in das Freie hinaus, und die zurückgeworfene Welle ist deshalb nicht ganz so intensiv, wie die ankommende gewesen ist; vielmehr nimmt die Intensität der in der Röhre hin- und hergeworfenen Wellen kontinuierlich ab und sie erlöschen endlich, wenn nicht durch irgend eine anderweitige Einwirkung ihnen bei jedem Hin- und Hergange die verlorene Arbeit ersetzt wird. Was zu ersetzen ist, ist aber der Kegel nach nur ein kleiner Teil der ganzen lebendigen Kraft der Wellenbewegung, nur so viel, als bei der Reflexion an den offenen Enden verloren geht. Der verloren gehende Bruchteil der Amplitude am offenen Ende einer zylindrischen Röhre vom. innern Radius R bei einem Tone von der Wellenlänge l beträgt nach der Theorie
Dieser Verlust an lebendiger Kraft kann nun in verschiedener Weise ersetzt werden. Wenn in einen mit Luft unter dem Drucke p gefüllten Raum noch das kleine Volumen dV, welches unter dem Drucke p0 stand, hinübergedrängt wird, so ist die dazu nötige Arbeit gleich (p — p0) d V. Wenn also während der Schallschwingungen an Orten und zu Zeiten, wo die Luft verdichtet ist, entweder regelmäßig eine kleine Menge Luft hineingedrängt wird, oder durch Erhitzung der Druck der zusammengedrängten Luft gesteigert wird, so erzeugt diese Luftmasse bei ihrer Ausdehnung einen größeren Betrag lebendiger Kraft, als durch ihren Widerstand gegen die Verdichtung bei deren Zustandekommen verloren gegangen ist. Die erstere der beiden Ursachen wirkt in den Zungenpfeifen, letztere in den Röhren der Gasharmonika, wo mit der in das Rohr zurückströmenden Luft auch eine vergrößerte Gasmenge aus dem Gasrohr einströmt, und diese dann verbrennend den Druck während der Zeit der Wiederausdehnung steigert.
Die Bedingungen, welche erfüllt sein müssen, damit Zungenpfeifen ansprechen, habe ich in den Verhandlungen des naturhistorisch-medizinischen Vereins zu Heidelberg (26. Juli 1861) gegeben3), und ich erlaube mir die kurze Auseinandersetzung mit einigen Verbesserungen hier wieder abdrucken zu lassen.
Unter Zungenpfeifen verstehe ich alle solche Blasinstrumente, in denen dem Luftstrom der Weg durch einen schwingenden elastischen Körper bald geöffnet, bald verschlossen wird. Die erste Arbeit, welche die Mechanik der Zungenpfeifen zugänglich machte, war die von W. Weber. Er experimentierte aber hauptsächlich mit metallenen Zungen, die wegen ihrer großen Masse und Elastizität nur dann von der Luft kräftig bewegt werden, wenn sich der von der Pfeife angegebene Ton nicht zu sehr von dem Eigenton der freien Zunge unterscheidet. Daher sind die Pfeifen mit metallenen Zungen in der Kegel nur fähig einen einzigen Ton anzugeben, nämlich nur denjenigen unter den theoretisch möglichen Tönen, welcher dem eigenen Ton der Zunge am nächsten liegt.
Anders verhält es sich mit Zungen von leichtem, wenig Widerstand leistendem Material, wie es die Rohrzungen der Klarinette, Oboe, des Fagotts, die menschlichen Lippen in den Trompeten, Posaunen, Hörnern sind. Sehr geeignet für die Versuche sind auch membranöse Zungen aus vulkanisiertem Kautschuk, ähnlich den Stimmbändern des Kehlkopfs gestellt; nur muß man sie, damit sie leicht und gut ansprechen, schräg gegen den Luftstrom stellen,
Die Wirkung der Zungen ist wesentlich verschieden, je nachdem die von ihnen geschlossene Öffnung sich öffnet, wenn sich die Zunge dem Winde entgegen nach der Windlade zu bewegt, oder wenn sie sich mit ihm gegen das Ansatzrohr bewegt. Die ersteren nenne ich einschlagende Zungen, die letzteren ausschlagende. Die Zungen der Klarinette, Oboe, des Fagotts, der Zungenwerke der Orgel sind alle einschlagende Zungen. Die menschlichen Lippen in den Blechinstrumenten repräsentieren dagegen ausschlagende Zungen. Die von mir gebrauchten Kautschukzungen kann man einschlagend und ausschlagend stellen.
Die Gesetze für die Tonhöhe der Zungenpfeifen ergeben sich vollständig, wenn man die Bewegung der Zunge unter dem Einflusse des periodisch wechselnden Luftdrucks im Ansatzrohr und Windrohr bestimmt, und berücksichtigt, daß das Maximum der Geschwindigkeit der ausströmenden Luft nur erreicht werden kann, wenn die von der Zunge gedeckte Öffnung ihre größte Weite erreicht hat.
l) Zungen mit zylindrischem Ansatzrohr ohne Windrohr. Die Zunge wird betrachtet als ein Körper, der durch elastische Kräfte in seine Gleichgewichtslage zurückgeführt wird, und durch den, wie der Sinus der Zeit periodisch wechselnden Druck im Ansatzrohr wieder daraus entfernt wird. Die Bewegungsgleichungen4) zeigen, daß der Augenblick stärksten Drucks in der Tiefe des Ansatzrohres fallen muß zwischen eine größte Elongation der Zunge nach außen, die ihm voraufgeht, und eine größte Elongation nach innen, welche nachfolgt. Wenn man nun die Schwingungsdauer gleich der Peripherie eines Kreises in 360 Grade abgeteilt denkt, so ist der Winkel e , um welchen das Maximum des Druckes vor dem Durchgang der Zunge durch ihre Mittellage eintritt, gegeben durch die Gleichung
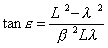
4) Ähnlich zu behandeln, wie Seebeck's Theorie des
Mittönens. Repertorium der Physik VIII, 60 bis 64. Siehe auch dieses
Werk, Beilage IX, Gleichung 4c. Das dortige s ist aber das Komplement des
obigen zu einem Rechten und statt der Schwingungszahlen sind hier die Wellenlängen
gesetzt.
In derselben Weise muß nun die Zeit bestimmt werden, um welche der größte Druck in der Tiefe des Ansatzrohres abweicht von der größten Geschwindigkeit, welche letztere wieder zusammenfallen muß mit derjenigen Stellung der Zunge, wo die Öffnung am weitesten ist. Die Berechnung dieser Größe ergibt sich aus meinen Untersuchungen über die Luftbewegung im Innern eines offenen zylindrischen Rohrs5). Das Maximum der nach der Mündung gerichteten Geschwindigkeit geht dem Maximum des Drucks voraus um einen Winkel d (die Schwingungsdauer als Peripherie eines Kreises betrachtet), der gegeben ist durch die Gleichung
5) Journal für reine und angewandte Mathematik LVII.
Wiss. Abh. Bd. I, S. 303.
Da nun Luft in das Ende des Ansatzrohrs nur eintreten kann, wenn die Zunge geöffnet ist, so muß bei einschlagenden Zungen das Maximum der nach außen gerichteten Geschwindigkeit der Luft zusammenfallen mit der größten Elongation der Zunge nach innen, es muß also sein
Bei ausschlagenden Zungen dagegen muß das Maximum der Luftausströmung zusammenfallen mit der größten Elongation der Zunge nach außen, es muß sein
Da Q und b2 sehr kleine
Größen sind, kann ![]() nur in dem Falle einen erheblichen Wert annehmen, wenn l2
—
L2 sehr klein ist, also der Ton der Pfeife dem der freien
Zunge nahe kommt, wie das bei den metallenen Zungen meist der Fall
ist. Der Wert von l bestimmt sich dabei aus
der Gleichung l.
nur in dem Falle einen erheblichen Wert annehmen, wenn l2
—
L2 sehr klein ist, also der Ton der Pfeife dem der freien
Zunge nahe kommt, wie das bei den metallenen Zungen meist der Fall
ist. Der Wert von l bestimmt sich dabei aus
der Gleichung l.
Wenn aber der Unterschied beider Töne l
- L groß ist, muß im Gegenteil ![]() sehr klein sein, also nahehin
sehr klein sein, also nahehin
Der Druckwechsel in der Tiefe des Ansatzrohrs ist nun proportional ![]()
also ein Minimum, wenn
Von dieser Art sind die Töne der Klarinette; auch membranöse einschlagende Kautschukzungen an Glasröhren bis zu 16 Fuß Länge sprechen leicht an und lassen verschiedene Obertöne hervorbringen, die der Gleichung (l) gut entsprechen. Ausschlagende Zungen müssen sehr tief gestimmt sein, um reine Töne des Rohrs zu geben, daher die menschlichen Lippen dazu geeignet sind, in denen die elastischen Faserzüge mit einer großen Masse wässerigen unelastischen Gewebes belastet sind. Zylindrische Glasröhren können leicht wie Trompeten angeblasen werden und geben die Töne einer gedackten Pfeife. Von diesen sind die höheren, in denen die Differenz L2 — l2 groß ist, fest anzugeben, und rein gestimmt, die unteren dagegen nicht ganz unabhängig vom Werte von L, d.h. der Spannung und Dicke der Lippen, daher unsicher und veränderlich.
2) Zungen mit kegelförmigem Ansatzrohr ohne Windrohr. Es findet ein sehr merkwürdiger Unterschied statt zwischen zylindrischen und kegelförmigen Ansatzröhren. Die Luftbewegung im Innern der letzteren läßt sich nach denselben Grundsätzen bestimmen, welche ich für die zylindrischen Röhren gebraucht habe. Man setzt innerhalb des Rohrs das Potential der Luftbewegung gleich
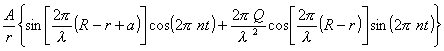
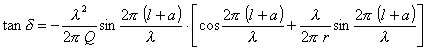
Ich gebe hier folgend die Reihe der ans Gleichung) berechneten Töne für eine kegelförmige Röhre aus Zink, welche folgende Maße hatte:
Länge l = 122,7 cm.
Durchmesser der Öffnungen 5,5 und 0,7 cm.
Reduzierte Länge l + a, berechnet 124,77 cm.
| Ton | Wellenlänge berechnet |
|
|
|
|
|
||
|
|
|||
| l) H — | 283,61 = | 2/1×141,80 | = 4/1 × 70,90 |
| 2) h — | 139,83 = | 2/2 × 139,84 | = 4/3 × 104,88 |
| 3) fis1 | 91,81 = | 2/3 × 137,71 | = 4/5 ×114,76 |
| 4)h1 + | 67,94 = | 2/4 × 135,88 | = 4/7 × 118,89 |
| 5) dis2 | 53,76 = | 2/5 × 134,39 | = 4/9 × 120,95 |
| 6)g2 | 44,40 = | 2/6 × 133,21 | = 4/11 × 122,11 |
| 7) b2 — | 37,79 = | 2/7 ×132,26 | = 4/13 × 122,82 |
| 8) c3 | 32,87 = | 2/8 × 131,50 | = 4/15 × 123,28 |
| 9) dis3 | 29,22 = | 2/9 × 131,47 | = 4/17 × 124,17 |
Die Töne vom 2ten bis 9ten konnten beobachtet werden, und fanden sich vollständig übereinstimmend mit der Rechnung. Man sieht aus den beiden letzten Rubriken, daß die hohen Töne sich fast genau denen einer gedackten Pfeife anschließen, deren Länge der reduzierten Länge der Röhre 124,7 gleich ist; die tieferen schließen sich näher an die einer offenen Pfeife, deren Länge bis zur Spitze des Kegels reichte. Die reduzierte Länge einer solchen wäre R + a == 142,6 Ctm. Gewöhnlich werden die Töne der Blechinstrumente den Tönen einer offenen Pfeife gleich gesetzt, aber die oberen sind verhältnismäßig zu tief gegen die unteren, in unserem Falle um mehr als einen halben Ton. Bei den Trompeten und Hörnern wird dieser Fehler vielleicht einigermaßen durch den Schallbecher an der Mündung korrigiert. Bei den Posaunen helfen die Auszüge nach.
Während die Trompeten, Posaunen und Hörner zu den Zungenwerken dieser Klasse mit kegelförmigem Rohr und tiefen ausschlagenden Zungen gehören, tragen die Oboen und Fagotte hohe einschlagende Zungen. Sie geben bei der Überblasung ebenfalls die höhere Oktave und dann die Duodecime, wie eine offene Pfeife. Die Rechnung nach Gleichung (2) stimmt für die Oboe sehr gut mit Zamminer's Messungen.
II. Das Anblasen der Flötenpfeifen.
In meiner Abhandlung über diskontinuierliche Flüssigkeitsbewegungen (Monatsberichte der Akademie der Wissenschaften zu Berlin vom 23. April 18686) habe ich die mechanischen Eigentümlichkeiten solcher Bewegungen beschrieben und aus der Theorie abgeleitet, wie sie der (auf S. 154 beschriebene) blattförmige Luftstrom an der Mündung einer angeblasenen Orgelpfeife ausführt. Die Grenzflächen dieser Schicht, welche die in die Mundöffnung der Pfeife ein- und ausströmende Luftmasse quer durchbricht, sind als Wirbelflächen zu betrachten, das heißt als Flächen, die mit einer kontinuierlichen Schicht von Wirbelfäden belegt sind. Solche Flächen haben ein sehr leicht störbares Gleichgewicht. Eine ebene Fläche dieser Art, gleichmäßig mit parallelen geraden Wirbelfäden bedeckt, von unendlicher Ausdehnung könnte bestehen; wo aber die geringste Ausbiegung erst einmal eingetreten ist, rollt sie sich in immer enger sieh zusammenziehende Spiralwindungen auf, welche immer weiter greifende Teile der Fläche in ihren Wirbel hineinziehen.
7) J. Tyndall: "On Sound". Deutsche Übersetzung, Braunschweig 1874. 8. 274 bis 292. — Derselbe im "Philosophical Magazine" Ser. IV, Vol. XXXIII, 92 bis 99 und 375 bis 391.
Diese Auflösung in Wirbel findet an dem Luftblatt der Pfeifenmündungen da statt, wo es gegen die Lippe der Pfeife schlägt. Von dieser Stelle ab löst es sich in Wirbel auf, wobei es sich mit der umgebenden oszillierenden Luft der Pfeife mischt. Je nachdem es ein- oder auswärts strömt, verstärkt es deren nach innen oder nach außen gerichtete Geschwindigkeit und wirkt also wie eine beschleunigende Kraft von periodisch wechselnder entgegengesetzter Richtung, die sehr schnell von der einen nach der anderen Seite umschlägt. Den transversalen Oszillationen der umgebenden Luftmasse folgt ein solches Luftblatt ohne erheblichen Widerstand. Während der Phase des Einströmens der Luft in die Mündung der Pfeife wird auch das Luftblatt einwärts gerichtet und verstärkt nun seinerseits wieder die lebendige Kraft des Einströmens. Umgekehrt, während des Ausströmens8).
8) Die Bildung
dieses Luftblattes und seines Schwingens ist von den Herren Schneebeli
(Poggendorff's Annalen Bd. 153, S. 301), Sonreck (ebenda Bd. 158,
S. 129) und Hermann Smith (English Mechanic January 1867; Nature
Vol. VIII, p. 25, 45, 383, Vol. IX, p. 301, Vol. X, p. 161, 481, Vol. XI,
p. 325) beschrieben, auch hat schon der erstgenannte die mechanische Erklärung
für die wesentlichen Züge dieses Vorgangs gegeben.
Wenn man die beschleunigende Kraft des Luftstroms durch eine Fourier'sche
Reihe dargestellt denkt, so werden nach dem (auf Seite 57) erwähnten
Gesetze die Amplituden der einzelnen Glieder von der Ordnungszahl m
im Allgemeinen abnehmen wie ![]() .In
der Tat braucht man nur den in Beilage
III Gleichung (1b) und (3) gegebenen Ausdruck für die Elongation
y
einer gezapften Saite zu benutzen, um für die Zeit t = 0 den
Wert von
.In
der Tat braucht man nur den in Beilage
III Gleichung (1b) und (3) gegebenen Ausdruck für die Elongation
y
einer gezapften Saite zu benutzen, um für die Zeit t = 0 den
Wert von ![]() zu bilden, so bekommt man die Reihe, welche den periodischen Wechsel zwischen
einem höheren und einem niederen Werte des y ausdrückt,
wie ihn Fig. 19 (auf
Seite 94) darstellt.
zu bilden, so bekommt man die Reihe, welche den periodischen Wechsel zwischen
einem höheren und einem niederen Werte des y ausdrückt,
wie ihn Fig. 19 (auf
Seite 94) darstellt.
Aus meinem oben zitierten Aufsatze über die Luftschwingungen in Röhren mit offenen Enden ergibt sich, daß überall in der Röhre eine positive Komponente des Drucks zusammenfällt mit dem Maximum der gegen die Öffnung gekehrten Geschwindigkeit, welche mit dieser Geschwindigkeit multipliziert den Wert hat:
A das Maximum der Geschwindigkeit am Ende der Röhre,
Q den Querschnitt des zylindrischen Teils der Röhre,
![]() , und l
die Wellenlänge.
, und l
die Wellenlänge.
Die Umstände, welche auf den Mechanismus des Anblasens und den Wert der Größe b Einfluß haben, erfordern eine weitläufigere Erörterung. Ich hoffe letztere bald an einem anderen Orte geben zu können.