Herstellung einfacher Töne durch Resonanz.
Die Theorie der Resonanz lufthaltiger Röhren und Hohlräume, so weit. sie bisher mathematisch ausführbar erschien, habe ich gegeben in meinem Aufsatze: Theorie der Luftschwingungen in Röhren mit offenen Enden, in Crelle's Journal für Mathematik Bd. LVII. Eine Vergleichung der Obertöne von Stimmgabeln und dazu gehörigen Resonanzröhren findet sich in meinem Aufsatze: Über Kombinationstöne in Poggendorff's Annalen Bd. XCIX, S. 509 und 510 1).
1) Die dort erwähnten harmonischen Obertöne der in der Nähe einer Stimmgabel schwingenden Luft sind auch von Herrn Stefan (Sitzungsber. d. Wiener Akad. Bd. LXI, 2. Abth., S. 491 bis 498) und von Herrn Quincke (Poggendorff's Annalen Bd. 28) mit dem Interferenzapparate beobachtet. Wiss. Abh. Bd. I, S. 303 und Bd. I, S. 263.
Ich füge hier gleich die Maße der S. 95 erwähnten Resonanzröhren
hinzu, welche für mich von Herrn Fessel in Köln in Verbindung
mit den später zu besehreibenden elektromagnetisch bewegten Stimmgabeln
verfertigt waren. Dies waren zylindrische Röhren von Pappe; die Grundflächen
des Zylinders waren ans Scheiben von Zinkblech gemacht, die eine ganz verschlossen,
die andere mit einer runden Öffnung versehen. Diese Röhren hatten
also überhaupt nur eine Öffnung, nicht zwei, wie die Resonatoren,
welche bestimmt sind, an das Ohr gesetzt zu werden. Eine fertige Resonanzröhre
solcher Art kann man tiefer machen, wenn man ihre Öffnung verengert.
Um sie, wo es nötig war, höher zu machen, habe ich etwas Wachs
hineingeworfen, und ihre geschlossene Grundfläche auf einen heißen
Ofen gestellt, bis das Wachs geschmolzen war und sich über den Boden
gleichmäßig ausgebreitet hatte. Man läßt es dann
in derselben Stellung der Röhre erkalten. Ob eine Röhre etwa
zu hoch oder zu tief für ihre Stimmgabel ist, prüft man, indem
man ihre Öffnung ein wenig verdeckt, während die schwingende
Stimmgabel vor ihr steht. Wird die Resonanz stärker durch Zudecken,
so ist die Röhre zu hoch gestimmt. Fängt dagegen gleich vom Beginn
des Zudeckens die Resonanz an sehr entschieden abzunehmen, so ist die Röhre
meist etwas zu tief gestimmt. Die Maße in Millimetern sind folgende:
| Nro. | Tonhöhe | Länge der Röhre | Durchmesser der Röhre | Durchmesser der Öffnung |
| l | B | 425 | 138 | 31,5 |
| 2 | b | 210 | 82 | 23,5 |
| 8 | f’ | 117 | 65 | 16 |
| 4 | b’ | 88 | 55 | 14,3 |
| 5 | d" | 58 | 55 | 14 |
| 6 | f" | 53 | 44 | 12,5 |
| 7 | as" | 50 | 39 | 11,2 |
| 8 | b" | 40 | 39 | 11,5 |
| 9 | d"’ | 35 | 30,5 | 10,3 |
| 10 | f"’ | 26 | .26 | 8,5 |
Die Theorie des Mitschwingens der Saiten läßt sich am besten an dem Seite 95 besprochenen Versuche entwickeln. Wir behalten die in Beilage III gewählten Bezeichnungen bei, und nehmen an, daß das Ende der Saite, für welches x = 0, mit dem Stiel der Stimmgabel verbunden sei und dessen Bewegung mitmachen müsse. Diese sei gegeben durch die Gleichung
1) Der Druck der Saite, welcher bald größer, bald kleiner
wird, je nach dem Winke], unter welchem das Endstück der Saite gegen
den Steg gerichtet ist. Die Tangente des Winkels, welcher zwischen der
veränderlichen Richtung der Saite und ihrer Gleichgewichtslage eingeschlossen
ist, ist ![]() ,
und wir können deshalb den veränderlichen Teil des Druckes setzen
gleich
,
und wir können deshalb den veränderlichen Teil des Druckes setzen
gleich
2) Die elastische Kraft des Resonanzbodens, welche den Steg in seine Gleichgewichtslage zurückzuführen strebt, können wir setzen gleich - f2 y.
3) Der Resonanzboden, der sich mit dem Stege bewegt, erleidet Widerstand
von der Luft, an die er einen Teil seiner Bewegung abgibt; wir können
annähernd den Luftwiderstand der Geschwindigkeit seiner Bewegung proportional
setzen, also gleich ![]() .
.
Dadurch erhalten wir für die Bewegung des Steges, dessen Masse M sein mag, und für die entsprechende des darauf ruhenden Endes der Saite:
+ F sin (px) sin (mt) + G sin (px) cos (mt)………………..(7)
Um die Gleichung (l) zu erfüllen muß hierin sein:
= - A[(f 2 - Mm2) cos pl - pS sin(pl)] (8a)
Fmg2sin (pl) + G [(f 2
- Mm2) sin (pl) + pS cos (pl)]
= - Ag2m cos(pl)
![]()
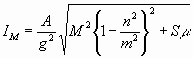 ,
,Wenn m > n, was in der Kegel der Fall sein wird, so ist es vorteilhaft, das Gewicht des Steges M ziemlich groß zu machen. Ich habe ihn deshalb aus Kupferblech verfertigt. Wenn M sehr groß ist, wird k [nach (8b)] sehr klein, und die Gleichung (9 a) ergibt dann, daß die verschiedenen Töne stärkster Resonanz sich desto mehr denjenigen Wert en nähern, welche der Reihe der einfachen ganzen Zahlen entsprechen. Je schwerer der Steg, desto besser ist die Saite abgegrenzt.
Die hier gegebenen Regeln über den Einfluß des Steges gelten aber zunächst nur für die angegebene Art der Erschütterung durch eine Stimmgabel, nicht für andere Arten, die Saite zu erregen.