IV. Prinzipien der experimentalen
Untersuchung, Maß und Methoden.
Folgendes die Betrachtung, von der ich bei diesen
Untersuchungen ausgegangen bin.
Gesetzt, es gelte zu beweisen, dass die Symmetrie
an sich wohlgefälliger als die Nichtsymmetrie ist, so hatte man nicht
an Bauwerke und den menschlichen Körper zu appellieren; da möchte
der Beweis immer zweifelhaft bleiben, so viel man messen wollte. Nach horizontaler
Richtung herrscht die Symmetrie in diesen Beispielen vor, nach vertikaler
fehlt sie, ausnahmsweise selbst nach horizontaler; und fraglich bleibt,
was dabei auf Wohlgefälligkeit an sich, was auf Zweckmäßigkeit
und andere Mitbestimmungen zu rechnen. Aber man kann die Entscheidung durch
die einfachste vergleichsweise Vorlage symmetrischer und nicht symmetrischer
Figuren erhalten, von denen möglichst Alles abgesondert ist, was außer
der Symmetrie und Nichtsymmetrie noch auf den Vorzug des Gefallens Einfluß
haben kann. Jedes nicht gar zu kleine Kind wird die einfache symmetrische
Figur der nicht symmetrischen, die kaleidoskopische Ordnung bunter Steinchen
ihrer Untereinanderwürfelung vorziehen, jeder Erwachsene beistimmen.
Warum nun nicht eben so einfach über den Vorzug des goldnen Schnittes
oder der einfachen rationalen Verhältnisse vor andern Verhältnissen
entscheiden? Tut es der goldne Schnitt der Symmetrie an Wohlgefälligkeit
gleich oder überbietet er sie gar, so muß sich dies auch schon
bei Versuchen mit einfachen Rechtecken und Abteilungen einfacher Längen
oder Streifen zeigen, wo keine Wahl zwischen einer verschiedenen Anlegungsweise
der Masse und keine Mitbestimmung durch Zweckrücksichten usw. statt
findet, oder alle philosophische Begründung und empirische Berufung
auf komplizierte Beispiele fruchtet nicht.
Auch wenn der Vorzug direkter Wohlgefälligkeit
des Taktes vor der Taktlosigkeit, d. i. der Regel vor der Regellosigkeit
in Wiederholung von Toneindrücken oder Bewegungen, bewiesen werden
sollte, würde die Berufung auf die Leistungen des Taktes in der Musik
und beim Tanze nicht entscheiden, da es gegenteils manche Geschäfte
gibt, die ihrer Natur nach besser ohne bestimmten Takt ausgeführt
werden, wo uns die gesuchte Durchführung des Taktes vielmehr mißfällt,
so schon bei der freien Rede; denn hiernach könnte man umgekehrt auf.
Mißfälligkeit des Taktes schließen. Aber der einfachste
Vergleich eines bedeutungslosen, sei es rhythmisch gegliederten oder selbst
ganz einförmigen, Taktschlages mit einem das Zeitmaß regellos
wechselnden Schlage oder Geräusche (wozu taktförmiges und regelloses
Trommeln mit den Fingern dienen kann), führt zur Entscheidung, bei
der nicht mehr die Frage ist, ob es das Eingehen in eine, das ästhetische
Gefühl aus andern Gesichtspunkten interessierende, Beschäftigung
und die Förderung dieser Beschäftigung, oder die Beschäftigung
durch den Takt selbst ist, was denselben wohlgefälliger als die Taktlosigkeit
erscheinen läßt.1) Ist aber
die Entscheidung für den Vorteil des, von ästhetischen Mitbestimmungen
entleerten, Taktes solchergestalt gewonnen, so kann man dann seine Leistung
auch beim Zutritt von solchen voraussehen, nicht freilich nach einfacher
Zufügung dessen, was er für sich leistet, zur Leistung der Mitbestimmungen,
aber unter Zuziehung des ästhetischen Hilfsprinzips; wonach er die
Wohlgefälligkeit jedes Geschäftes, in das er fördernd oder
verträglich hineintritt, sogar mehr steigern wird, als man nach seiner
abstrakten Leistung voraussetzen könnte, indes seine Wohlgefälligkeit
sonst durch die Mißfälligkeit der Hinderung des Geschäftes
leicht überboten wird.
1) Man bemerkt vielleicht hiergegen, dass ein fortgesetzter
leerer Taktschlag ermüdend langweilig sei. Das ist wahr, aber auch
das schönste Kunstwerk langweilt, wenn man es fortgesetzt betrachten
soll; ein regellos den Takt wechselnder bedeutungsleerer Schlag aber wird
auf die Länge nicht bloß langweilig, sondern unaussteh-lich
und greift die Nerven an. Mag man also den Vergleich des Taktes mit dem
regellos wechselnden Geräusche oder Schlage auf kurze oder lange Zeit
ausdehnen, immer wird der erste in Vorteil bleiben, und dieser Vorteil
konstatiert werden können, ohne dass man ein taktmäßiges
Geschäft mit einem taktlosen vergleicht.
Ich habe hier Beispiele vorgeführt, bei denen die
Entscheidung über den Vorteil direkter Wohlgefälligkeit nach
einer bestimmten Seite leicht und einfach ist, weil der Vorteil verhältnismäßig
groß ist. Das ist aber nicht überall der Fall. Niemand von gesunder
Empfänglichkeit wird die Asymmetrie der Symmetrie, die Taktlosigkeit
dem Takte bei reinem Vergleiche ihrer direkten Wirkung vorziehen, während
nichts weniger als alle bei entsprechendem Vergleiche den goldnen Schnitt
als Dimensionsverhältnis den davon abweichenden Verhältnissen
vorziehen, weil sein Vorteil verhältnismäßig minder groß
ist, ungeachtet er einen Vorteil hat. Aber das ändert das Prinzip
möglichster Isolierung direkter Wirkung bei den Versuchen nicht, soll
überhaupt über die direkte Wirkung ins Klare gekommen werden,
sondern läßt um so mehr auf der Isolierung bestehen, und führt
nur mit, dass, während es bei obigen Beispielen keiner großen
Anzahl von Stimmen bedarf, um die Entscheidung sicher zu stellen, sofern
Alle sich in derselben Richtung und Entschiedenheit des Vorzugs vereinigen,
man hier auf wenige Stimmen nichts Sichres bauen kann, weil ohne festgebotene
Mitbestimmungen doch zufällige Mitbestimmungen von Innen und
Außen ins Spiel treten, welche einen geringen Vorteil der Wohlgefälligkeit
an sich eben so leicht gegenwirkend überbieten als gleichsinnig wirkend
steigern, hiermit das Vorzugsurteil leicht auch auf ein an sich minder
wohlgefälliges Verhältnis, dem aber günstigere zufällige
Mitbestimmungen zu statten kommen, fallen lassen können. Also hat
man das Urteil möglichst Vieler zuzuziehen, wobei Folgendes in Rücksicht
kommt:
Je größer allgemein gesprochen die Wohlgefälligkeit
eines bestimmten Verhältnisses an sich ist, desto schwerer werden
es gegenwirkende zufällige Mitbestimmungen finden, die Wirkung dieser
Wohlgefälligkeit zu überbieten, desto leichter die gleichsinnig
wirkenden, das Übergewicht seiner Wohlgefälligkeit über
andre Verhältnisse fortzuerhalten, indem sie es sogar steigern; also
werden desto mehr Personen es andern vorziehen; die meisten aber dasjenige
unter allen vorziehen, welches unter allen das an sich wohlgefälligste
ist.2) Wenn die Wohlgefälligkeit eines
bestimmten Verhältnisses an sich sehr überwiegend gegen die Wohlgefälligkeit
der mit ihm konkurrierenden Verhältnisse ist, so werden gegenwirkende
zufällige Mitbestimmungen überhaupt nicht vermögen, dies
Übergewicht zu überwinden, dann wird das betreffende Verhältnis
sogar immer und von Allen vorgezogen werden; wogegen, wenn
sein direktes Wohlgefälligkeitsübergewicht verschwindend klein
oder null gegen die konkurrierenden wäre, die zufälligen Mitbestimmungen
es eben so leicht finden, das Übergewicht nach der einen als andern
Seite zu lenken, so dass das betreffende Verhältnis eben so oft andern
vorgezogen als andern nachgesetzt wird. Allgemein also wird die relative
Zahl der Bevorzugungen eines Verhältnisses mit dem Grade der Wohlgefälligkeit,
welchen dasselbe abgesehen von zufälligen Mitbestimmungen hat, wachsen
und abnehmen.3)
2) Die Wahrscheinlichkeit nämlich, dass zufällige
Einflüsse in gleichem Sinne bis zu einem gewissen Werte zusammentreffen,
wird um so geringer, je größer dieser Wert ist; und hängt
nach einem gewissen Gesetze von dessen Größe ab. Also haben
auch die, einem Überschusse direkter Wohlgefälligkeit entgegenwirkenden,
zufälligen Mitbestimmungen um so weniger Wahrscheinlichkeit, bis zu
der Größe zu gelangen, wodurch sie diesen Überschuß
über ein konkurrierendes Verhältnis kompensieren oder überbieten,
und mithin das konkur-rierende Verhältnis vorziehen lassen, je größer
der Wohlgefälligkeitsüberschuß darüber an sich ist.
3) Dass hierbei keine Proportionalität vorausgesetzt wird, ist weiterhin
besprochen.
Hierauf nun gründet sich unser Maß, gründen
sich unsre Aufgaben und unsere Methoden wie folgt:
Direkt kann man den Grad der Wohlgefälligkeit
oder Mißfälligkeit, unter dem ein Verhältnis diesem oder
jenem unter diesen oder jenen Umständen erscheint, nicht messen; dazu
gelte es ein Maß der Einzel-Lust und Unlust zu haben, was wir noch
nicht haben; aber man kann das Maß andershin übertragen, indem
man die Personen zählt, die dem einen und die dem andern Verhältnisse
bei gleichzeitiger Vorlage derselben oder überhaupt gleicher Möglichkeit
der Wahl den Vorzug geben, und dasjenige Verhältnis für das wohlgefälligste
zunächst für die Klasse von Personen, die man zu den Versuchen
zugezogen hat, erklärt, welches die meisten Vorzugsstimmen für
sich vereinigt, oder, wenn es nicht mit vorliegt, ein solches, um welches
sich die Vorzugsstimmen am dichtesten schaaren4),
überhaupt aber den Grad der relativen Wohlgefälligkeit eines
gegebenen Verhältnisses für eine gegebene Menschenklasse nach
der relativen Zahl der sich dafür vereinigenden Stimmen dieser Klasse
beurteilt. Wiefern ein solches Urteil allgemeinere maßgebende Bedeutung
in Anspruch nehmen kann, wird weiterhin erörtert.
4) Von der Bestimmung eines solchen Verhältnisses wird es sich weiterhin
noch genauer handeln.
Gegen dies Maß der Wohlgefälligkeit wird
sich insofern kein Einwand aus aprioristischem Gesichtspunkte erheben lassen,
als es durch die Definition selbst a priori festgestellt ist. Ich nenne
nämlich nicht nur etwas nach Maßgabe wohlgefälliger, als
es unter vergleichbaren Bedingungen mehr Vorzugsstimmen für sich vereinigt,
sondern stelle auch ausdrücklich den Begriff größerer
oder geringerer Wohlgefälligkeit darauf; und rechtfertige dies von
einer Seite dadurch, dass es dem natürlichen Sprach- und Begriffsgebrauche
wirklich entspricht, etwas für wohlgefälliger zu erklären,
was die Eigenschaft hat, Mehreren wohlzugefallen, anderseits durch die
dadurch gebotene und bisher auf keine andere Weise zu erzielende Möglichkeit,
den Maßbegriff überhaupt in die Ästhetik einzuführen,
endlich durch die Vorteile der Einführung dieses Maßes. Denn
jedenfalls ist es ein fundamentales und für die Ästhetik fundamental
wichtiges Datum, zu wissen, in welcher Relation sich die bevorzugenden
Stimmen auf jeden Größenwert eines hinsichtlich seiner Wohlgefälligkeit
zu beurteilenden Verhältnisses verteilen, und so dient es nur der
Kürze, statt mit vielen Worten beispielsweise zu sagen, dass ein Verhältnis
doppelt so viel bevorzugende Stimmen vereinige, als ein anderes, zu sagen,
dass es doppelt so wohlgefällig gefunden werde. Auch lassen sich die
so erhaltenen Maßzahlen nicht minder in die Rechnung einführen
und dadurch verwerten, als irgend welche andere Maßzahlen, indes
sonst Angaben über ein Mehr oder Weniger der Wohlgefälligkeit
ganz unbestimmt bleiben.
Zwar kann man aus
allgemeinem Gesichtspunkte bemerken, dass, wenn eine Person von zwei Verhältnissen
das eine, eine andere Person das andere vorzieht, das Übergewicht
des Wohlgefallens, d. h. der Lust, die den Vorzug bei Auffassung des einen
und andern Verhältnisses bestimmt, bei der einen Person größer
sein kann, als bei der andern, und sollte es bei der geringeren Zahl von
Perso-nen, welche ein Verhältnis vorzieht, überall größer
sein, als bei der größern Zahl, welche das andere vorzieht,
so könnte die Lust der Auffassung des ersten Verhältnisses Seitens
der geringeren Zahl doch im Ganzen überwiegen.5)
Aber abgesehen, dass wir bei Zuziehung einer großen Zahl von Individuen
jenes "überall" gar nicht voraussetzen dürfen, bleibt schon die
Zahl der Bevorzugungen rücksichtslos auf die Intensität des dabei
zur Geltung kommenden Gefühles der einzelnen Subjekte, ein Element,
was messend in Betracht gezogen zu werden verdient. So kann man die Zahl
der Regen in einem gegebenen Monat des Jahres ohne Rücksicht auf die
Reichhaltigkeil des Regens messen, und hat daran schon ein nützliches
meteorologisches Datum.
5) Diese Betrachtung führt darauf, Lustquanta
überhaupt zu vergleichen, indes es der gewöhnlichen Betrachtung
Schwierigkeiten machen mag, solche nur zu statuieren, oder einen
Begriff damit zu verbinden. Wir umgehen nun diese Schwierigkeit mit unserm
Maße, doch mag beiläufig mit einigen Worten gezeigt werden,
dass eine prinzipielle Schwierigkeit in dieser Hinsicht eigentlich nicht
besteht. Da sich von größerer und kleinerer Lust sprechen läßt,
so muß sich auch von gleicher Lust sprechen lassen; und wenn nun
10 Menschen gleiche Lust an Etwas haben, so ist selbstverständlich
das Quantum oder die Summe dieser Lust zehnmal so groß, als die Lust
jedes Einzelnen von den Zehn. Nun ist allerdings die durch dieselbe Ursache
erregte Lust von 10 Menschen im Allgemeinen ungleich zwischen ihnen verteilt.
Nehmen wir aber 200 Menschen und versetzen sie unter gleiche Verhältnisse
zu einer bestimmten Ursache der Lust als 100 andere Menschen dieser Klasse;
so können wir voraussetzen, dass sich die Einzelverschiedenheiten
der Lust beiderseits im Ganzen merklich ausgleichen, und wieder sagen,
dass abgesehen von einem kleinen noch übrig bleibenden zufälligen
Unterschiede (woran die exaktesten Bestimmungen auch sonst laborieren),
das Lustquantum, was in den 200 Menschen durch die betreffende Ursache
erweckt wird, im Ganzen doppelt so groß sei, als was in den 100 erweckt
wird, wobei noch gar kein bestimmtes Maß der individuellen Lust vorausgesetzt
wird, sondern nur die Ausgleichung zufälliger Verschiedenheiten durch
die Zahl derselben. Erkennt man dazu an, dass es ein Maß der Einzellust
gibt, wenn auch bis jetzt noch nicht gefunden ist, nachdem es sich doch
für andere Fälle der Empfindung hat finden lassen , so kann man
auch sagen, dass das Lustquantum von 10 oder 100 Menschen, wie verschieden
und durch wie verschiedene Ursachen erweckt die Lust bei den Einzelnen
sei, 10-mal oder 100-mal so groß sei, als die Lust der Einzelnen
im Mittel, nur dass man, um den Begriff einer mittleren Lust zuzugestehen,
auch den Begriff des Einzelmaßes der Lust zuzugestehen hat. Jedenfalls
sieht man, dass mit Rücksicht auf die Verbreitungsfähigkeit der
Lust durch eine Mehrheit von Individuen dieselbe nicht schlechthin widerspenstig
gegen den Quantitätsbegriff ist.
Bei alledem dürfte
es nützlich sein, unser Maß der Wohlgefälligkeil als Maß
der extensiven Wohlgefälligkeit oder extensives Maß
der Wohlgefälligkeit von einem erst noch zu findenden Maße der
intensiven Wohlgefälligkeit oder intensiven Maße
der Wohlgefälligkeit zu unterscheiden, welches direkt auf den Grad
der Lust (oder auf Unterschiede im Grade der Lust) geht, die durch eine
gegebene Ursache bei den Einzelnen oder im Durchschnitt der Einzelnen erweckt
wird, ein Maß, welches nach den S. 43 geführten Betrachtungen
als in Abhängigkeit von der Zahl der Bevorzugungen, hiermit vom extensiven
Maße der Wohlgefälligkeit anzusehen, aber ihm deshalb doch nicht
proportional zu setzen ist.6)
Man kann hoffen, dass es noch gelingen wird, nach jener Abhängigkeit
das intensive Durchschnittsmaße selbst aus dem extensiven Maße
abzuleiten, und ich glaube den Weg dazu durch die Betrachtung S. 43 mit
Rücksicht auf die Wahrscheinlichkeitsgesetze des Zufalls vorgezeichnet
zu sehen; behalte mir aber erst noch eine bestimmtere Untersuchung und
Erklärung darüber vor. Hier bleiben wir jedenfalls bei dem extensiven
Maße stehen, welches seine klare, gesicherte und berechtigte Bedeutung
hat, indes der Begriff und die Bestimmungsweise des intensiven Maßes
bis jetzt noch als problematisch gelten können. Sollte sich das intensive
Maß finden lassen, so würde es eine viel tiefer greifende theoretische
Wichtigkeit für die Psychophysik als das extensive Maß haben,
dieses aber stets den Vorteil praktischer Anwendbarkeit vor ihm vorausbehalten
und auch als Basis für Ableitung des intensiven Maßes immer
zu schätzen sein.
6) Dies steht nicht in Widerspruch mit der in voriger
Anmerkung aufgestellten Ansicht, dass, wenn respektive 100 und 200 Menschen
derselben Klasse derselben Ursache der Lust gegenübergestellt werden,
das beiderseits erweckte Lustquantum der Zahl der Individuen proportional
gesetzt werden könne, da es sich vielmehr hier darum handelt, ob die,
durch verschiedene Ursachen (verschiedene Verhältnisgrößen)
erweckte Lust, welche den Vorzug der einen vor der andern Ursache, abgesehen
von zufälligen Mitbedingungen, bestimmt, der Zahl der Bevorzugungen
proportional gelten könne, was nicht vorauszusetzen ist. Man kann
sich auch dies am Regen erläutern. Aus langjährigen Beobachtungen
läßt sich finden, wie oft jeder Regen von bestimmter Wassermenge
in Verhältnis zum andern an einem gegebenen Beobachtungsorte vorkommt.
Aber weder die Wassermengen jedes einzelnen Regens selbst sind den Zahlen
ihres Vorkommens, noch die Unterschiede der Wassermengen jedes einzelnen
Regens den Unterschieden der Zahlen ihres Vorkommens proportional. Ein
Regen von einer bestimmten Wassermenge kommt voraussichtlich häufiger
als jeder andere vor, oder ist der, um welchen sich die Regen von bestimmter
Menge am dichtesten zusammendrängen, und nach Maßgabe als die
Wassermengen größer oder kleiner werden, nimmt die Zahl des
Vorkommens ab, aber in viel stärkerem Verhältnisse als die Wassermenge
selbst zu- oder abnimmt.
Mit voriger Bestimmung unseres Maßbegriffes stellen
die Aufgaben, die wir uns hier stellen können, in Beziehung. Erstens
wird zu untersuchen sein, ob unter den Werten eines der Variation unterliegenden
Formverhältnisses, abgesehen von festen ästhetischen Mitbestimmungen,
überhaupt einer ein (nicht bloß von unausgeglichenen Zufälligkeiten
abhängiges) Übergewicht der Vorzugszahl, hiermit ein Übergewicht
der Wohlgefälligkeit vor den davon abweichenden Werten hat, und welcher
es ist; – zweitens die Abnahme der Wohlgefälligkeit nach der
Abnahme der Vorzugszahlen bei gegebenen Abweichungen von dem wohlgefälligsten
Werte zu bestimmen und wo möglich das Gesetz der Abnahme zu finden;
– drittens, außer dem wohlgefälligsten Werte, welcher das Hauptinteresse
in Anspruch nimmt, noch einige andere, für die Beurteilung der Wohlgefälligkeitsverhältnisse
maßgebende Hauptwerte, wovon später, samt den Beziehungen dazwischen
aus den Maßzahlen abzuleiten; viertens, den Sicherheitsgrad
der Resultate zu bestimmen. Außer diesen Aufgaben, die ich kurz als
objektive zusammenfasse, kann man sich noch einige unten zu besprechende,
von mir so genannte subjektive Aufgaben stellen.
Zur Lösung dieser sämtlichen Aufgaben
stehen uns nun drei Methoden zu Gebote, die ich kurz als Methode der
Wahl, Methode der Herstellung und Methode der Verwendung
unterscheide, und zunächst nach ihrem Hauptgesichtspunkte wie folgt
charakterisiere.
Methode der Wahl. Man legt die, hinsichtlich
ihrer relativen Wohlgefälligkeit zu vergleichenden, Verhältnisse
in möglichst einfachen Schematen7) vielen Personen vor,
läßt sie, wenn es sich um direkte Wohlgefälligkeit handelt,
mit ausdrücklicher Erinnerung an keine bestimmte Verwendung zu denken,
das Verhältnis, was ihnen nach seiner eigenen Beschaffenheit am wohlgefälligsten
und was am mißfälligsten erscheint, bezeichnen, und trägt
jedes Vorzugsurteil so wie Verwerfungsurteil in eine, mit dem betreffenden
Verhältnisse übeschriebene, Columne, einer besondern Vorzugs-
und einer besondern Verwerfungstabelle ein, und zwar mit l, wenn der Vorzug
oder die Verwerfung sich für ein bestimmtes Verhältnis entscheidet,
hingegen mit 1/2 oder 1/3,
wenn zwischen 2 oder 3 Verhältnissen geschwankt wird, um endlich die
Zahlen jeder Columne der Vorzugs- wie Verwerfungstabelle besonders zusammenzuzählen
und zu vergleichen, wobei die weniger wichtigen (auch oft von mir nicht
zugezogenen) Verwerfungsurteile in sofern doch eine Art Kontrolle bieten
können, als die am seltensten vorgezogenen Verhältnisse zugleich
die am häufigsten verworfenen sein müssen, wenn die Methode in
sich stimmen soll.
7) Also z. B., wenn es sich um Dimensionsverhältnisse handelt, in
einfachen Rechtecken aus Karton.
Methode der Herstellung. Man veranlaßt
viele Personen, statt unter mehreren vorgegebenen Verhältnissen das
wohlgefälligste zu wählen, vielmehr dasselbe in einfachst
möglichen Schematen selbst herzustellen8),
wonach man untersucht, bei welchem Verhältnisse die meisten Versuchssubjekte
zusammentreffen oder um welches sich die einzelnen am dichtesten scharen;
die geringeren Grade der Wohlgefälligkeit aber nach der geringeren
Zahl derer, die bei einem gegebenen Verhältnisse stehen bleiben, mißt.
8) So lasse ich, bei Versuchen mit Kreuzen nach dieser
Methode, auf einem fest aufliegenden oder fest aufgeklebten Längsbalken
aus weißem oder schwarzem Karton einen losen Querbalken so lange
vorschieben, bis er die wohlgefälligste Höhenstellung zu haben
scheint; insofern sich aber diese nach dem Längenverhältnisse
der Balken ändert, variiere ich dies Verhältnis so wie das der
Breite der Balken in verschiedenen Versuchsserien. Ich lasse über
senkrechten Strichen von verschiedener Länge Punkte in der wohlgefälligsten
Höhe anbringen, wobei der Gedanke an ein J freigestellt ist, usw.
Methode der Verwendung. Man mißt die Dimensionen
oder Abteilungen der einfachsten, im Gebrauche, Verkehr, Handel
und Wandel, kurz will ich sagen, im Leben, vorkommenden Gegenstände,
bei welchen die Form vielmehr direkt durch Rücksichten der Wohlgefälligkeit
(vorausgesetzt, dass es sich um reine direkte Wohlgefälligkeit handelt)
als des Zwecks, der Bedeutung oder des Anpassens an andere Formen bestimmt
ist, und welche keine Willkür in der Anlegungsweise des Maßes
zulassen9), wonach man wieder das relative
Maß der Wohlgefälligkeit durch die relative Häufigkeit
des Vorkommens dieses oder jenes Formverhältnisses bestimmt hält.
9) So habe ich u. a. Glückwünschungskarten
und ähnliche Karten, deren Dimensionsverhältnisse nur durch direkte
Wohlgefälligkeitsrücksicht ohne angebbare assoziative und kombinatorische
Mitbedingungen bestimmt scheinen, in einer Mehrzahl von Luxuspapierfabriken
und Papierhandlungen, so wie Schmuckkreuze bei verschiedenen Juwelieren
in größerer Zahl gemessen. Bei Visitenkarten, die ich u. a.
auch in Untersuchung genommen, findet schon eine angebbare kombinatorische
Mitbestimmung durch die Streckung des Namens statt. Briefcouverts wechseln
in den Dimensionsverhältnissen sehr nach der Mode, indem sie dabei
wie manche andere Formen um das nach der Gesamtheit aller Versuche an sich
wohlgefälligste Verhältnis schwanken. Die Schmuckkreuze unterscheiden
sich, trotz ihres Ursprungs aus dem Kruzifixe, doch wesentlich von diesem,
indem der Zweck, der die Form des Kruzifixes bestimmt, bei dem Schmuckkreuz
gegen die Rücksicht direkter Formwohlgefälligkeit zurücktritt.
Weiteres und Genaueres über diese und andere Beispiele s. später
bei den Versuchen.
Jede der zwei ersten Methoden kann mit der dritten gewissermaßen
verbunden werden, insofern man, anstatt der Wahl oder Herstellung abstrakter
Formen ohne Rücksicht auf Anwendung ausdrücklich die Wahl oder
Herstellung mit dem Gedanken konkreter Anwendung vornehmen läßt,
wonach ich abstrakte und konkrete Methode der Wahl und Herstellung oder
auch reine Methode und Methode mit Verwendung unterscheide.
So viel als möglich wird man diese verschiedenen
Methoden sich durch einander ergänzen und wechselseits kontrollieren
lassen. Jede bedarf mannigfacher Vorsichten, Rücksichten und Rechnungshilfen,
wovon wir aber erst in folgenden Abschnitten sprechen, um zuvor noch verschiedene
allgemeine Gesichtspunkte teils in Bezug auf die Methoden selbst, teils
die denselben zu stellenden Aufgaben zu besprechen.
Bei jeder dieser Methoden erhält man, wenn
sie in einiger Vollständigkeit ausgeführt wird, eine Reihe durch
Wahl, Herstellung oder Verwendung vor den übrigen bevorzugter Dimensions-
oder Abteilungsverhältnisse, die ich allgemein mit v, die Zahl
der darauf fallenden Bevorzugungen aber mit z bezeichne. Die Bestimmtheit,
wie viel Bevorzugungen jedes v erfahren hat, welches z ihm
also zukommt, nenne ich die Verteilung der Werte v nach Maß
und Zahl oder kurz Verteilung schlechthin, und eine Tabelle, welche die
Werte v nach ihrer Größe geordnet mit dem darauf fallenden
z enthält, die Verteilungstabelle der v.
Aus gewissem Gesichtspunkte ordnet sich die Sammlung
der Werte v mit zugehörigen z, welche eine bestimmte
Versuchsreihe liefert, dem Begriffe eines in seinen Einzelexemplaren dem
Maße nach zufällig variierenden Kollektivgegenstandes unter,
wovon Natur und Kunst unzählige Beispiele liefern10),
über deren Verteilungsgesetze nach Maß und Zahl der Einzelwerte
ich anderwärts zu veröffentlichende Untersuchungen angestellt
und die Übertragbarkeit der dafür geltenden Bestimmungen auf
unser Untersuchungsgebiet, insbesondere nach Resultaten der zweiten und
dritten Methode, teils schon geprüft habe, teils noch Data dazu sammle.
Hierauf wird öfters im Folgenden Bezug genommen werden.
10) Es variieren z. B. Menschen von gegebenem Geschlecht,
Alter, Rasse – eben so mittlere Jahrestemperaturen oder Regenmengen an
einem gegebenen Orte – eben so die Dimensionen von Visitenkarten oder Galleriegemälden
– nach ihrer Größe, und jeder Größe kommt ein bestimmtes
z zu. Insofern aber diese Variationen von Zufälligkeiten abhängen,
unterliegen sie auch den allgemeinen Wahrscheinlichkeitsgesetzen eines
sich häufenden Zufalls nicht minder als die Variationen unserer v
in Betracht des Einflusses zufälliger Mitbestimmungen.
Wenn schon wir bei Darlegung unserer Methoden nur deren
Anwendbarkeit auf die Prüfung der reinen Formwohlgefälligkeit,
oder von uns so genannten direkten Wohlgefälligkeit einfachster Verhältnisse,
also abgesehen von assoziativen und kombinatorischen Mitbestimmungen ins
Auge gefaßt haben, da unsere Hauptaufgabe hier ausdrücklich
auf diese Prüfung gerichtet ist, geht doch die Anwendbarkeit dieser
Methoden viel weiter, sofern sie eben so zur Prüfung der Wohlgefälligkeit
von Formverhältnissen jeder Art unter irgend welchen Mitbe-dingungen
in irgend welchen Verwendungen, hiermit zur Weiterführung dieser Untersuchun-gen
dienen können; indem man nämlich methodisch vom Einfachem zum
Zusammengeset-ztern fortschreitend, die assoziativen und kombinatorischen
Mitbedingungen nach verschiedenen Richtungen variiert. Ja die erste Methode
kann selbst zur Bestimmung des Wohlgefälligkeitsvorzuges zwischen
Kunstwerken jeder Art, welche aus irgend einem Gesichtspunkte vergleichbar
sind, Anwendung finden, nur dass keine elementaren Bestimmungen und Gesetze
daraus zu schöpfen sind. Es dürfte aber oft nützlich sein,
dem vielfach geführten Streit, welches von zwei Kunstwerken das schönere
sei, durch die statistische Aussage der ersten Methode, welches in maßgebenden
Kreisen mehr Vorzugsstimmen erhalte, ein sichreres Fundament als das mehr
oder weniger subjektive einzelner Kennerstimmen zu geben.11)
11) Eine interessante Gelegenheit, von dieser Methode
im Kunstgebiete Gebrauch zu machen, böte sich u. a. bezüglich
des berühmten Streites über den Vorzug zwischen dem Dresdner
und dem Darmstädter Exemplare der Holbeinschen Madonna dar, welcher
bis zum Eintritte der jetzigen, dem Interesse an solchem Streite keinen
Raum mehr lassenden , Kriegszeiten im lebhaftesten Gange war, und nach
Beendigung derselben , insbesondere durch die noch zu erwartende Zusammenstellung
beider Exemplare in Dresden, unstreitig wieder neu angefacht werden wird,
ohne eines Endes gewärtig zu sein. Dazu müßte man bei der
öffentlichen Ausstellung beider Exemplare eine Abstimmungsliste über
den Vorzug des einen oder andern Exemplares auslegen, aus welcher nach
Abschluß derselben die Stimmen der Kunstkenner und Kunstlaien (so
weit sie wenn auch nur obenhin trennbar sind), der Männer und Frauen,
der Personen von verschiedener Nationalität (wobei eine etwaige sächsische
Parteilichkeit ihren Maßstab finden würde) und so beliebig weiter
zu sortieren, und die von jeder Kategorie gelieferten Vorzugsurteile für
das eine und andre Exemplar teils besonders zusammenzuzählen, teils
(zum Maßstab für das Durchschnittsurteil des gesamten kunstliebenden
Publikum) zur Totalsumme zu vereinigen wären. Das Hauptinteresse würde
dabei immer die Frage haben, welches von beiden Exemplaren Alles in Allem
genommen oder Eins ins Andre gerechnet den Vorzug Seitens dieser und jener
Kategorie so wie von der Gesamtheit erhielte, und in welchem Verhältnis
die entgegengesetzten Vorzugsstimmen gegen einander aufträten. Doch
könnten auch besondere Fragen über Spezialpunkte, die einem Spezialstreit
unterliegen, als namentlich bei unserm Beispiel über die Auffassung
der Madonna, die Proportionen in der Anordnung des Ganzen, das Kolorit
usw. gestellt werden. So erhielte man einen vergleichenden Maßstab
der wirklichen ästhetischen Leistung beider kapitalen Bilder für
verschiedene Menschenklassen nach verschiedenen Beziehungen aus verschiedenen
Gesichtspunkten statt der oft so einseitigen, befangenen und absprechenden
Einzelurteile mit einander hadernder Kenner, deren Resultat der einfache
Widerspruch gegen einander ist. Auch könnte unstreitig durch Aufnahme
des Planes und Gesichtspunktes der Abstimmung in das Programm der Ausstellung
das allgemeine Interesse für dieselbe und die Frequenz ihres Besuches
nur gesteigert werden. Nun zweifle ich zwar, dass dieser Vorschlag in Rücksicht
äußerer Bedenklichkeiten Erfolg haben wird; doch konnte er hier
dienen, die Tragweite unsrer Methode mit Beziehung auf das im Text Folgende
zu erläutern.
Nun ist freilich nicht außer Acht zu lassen, dass
man überall durch unsere Maßnahmen nur erfährt, wie sich
die relative Wohlgefälligkeit innerhalb der Klasse von Menschen stellt,
aus der man seine Versuchssubjekte entnommen hat, und naturlich ist weder
zu behaupten, noch zu erwarten, dass Kindern oder rohen Negern dasselbe,
was erwachsenen gebildeten Europäern, Ja nicht einmal, dass Frauen
durchschnittlich dasselbe, was Männern am besten gefällt. Aber
es hindert nicht nur nichts, die Unterschiede, die in dieser Hinsicht zwischen
verschiedenen Klassen von Menschen nach Alter, Geschlecht, Rasse, Stand,
Bildungsstufe, Klima, Zeitalter bestehen, zu verfolgen, indem man die Versuchssubjekte
danach sondert, sondern es muß dies selbst als eine wesentliche Aufgabe
der experimentalen Ästhetik gelten.
Natürlich aber wird man, wenn nach einem Verhältnisse
gefragt wird, welches Gebildete mehr als jedes andere befriedigt – und
nur ein solches wird Anspruch machen können, als Normalverhältnis
zu gelten, – auch Gebildete zum Urteil zuzuziehen haben, und, insofern
eine Spezialbildung oder Übung für die Auffassung des ästhetischen
Wertes eines Verhältnisses oder Werkes erfordert wird, solche Personen
zuzuziehen haben, welche diese Spezialbildung oder Übung besitzen,
um Urteile und damit Resultate nach unsern Methoden zu erhalten, welche
einen Wert haben, der dem entsprechend ist, den man dem Besitze solcher
Bildung und Übung selbst beilegt.
Gilt es namentlich die Beurteilung von Kunstwerken,
so wird auch eine gewisse Kunstbildung vorausgesetzt, um überhaupt
für die Empfindung des Wertes gewisser Seiten dieser Werke empfänglich
zu sein12), und wer ohne diese Bildung
darüber urteilt, kann durch die einseitige Berücksichtigung von
ästhetischen Vorteilen und Nachteilen, deren Auffassung keiner besonderen
Vorbildung bedarf, zu Urteilen geführt werden, die vor einer höheren
Abwägung nicht Stich halten. Selbst für die Auffassung des ästhetischen
Wertes so einfacher Verhältnisse, als um die es sich hier handelt,
wird die ästhetische Empfänglichkeit und Übung nicht ganz
gleichgültig sein, aber jedenfalls wird keine spezifische Bildung
dazu vorausgesetzt, und wenn man sich dabei an die allgemeine Klasse der
sog. Gebildeten hält, wird man Resultate erhalten, die dadurch, dass
sie den wirklichen ästhetischen Wert gegebener Verhältnisse
für diese Klasse herausstellen, auch Wert für diese Klasse haben.
12) Für die Vorzüge der Konzeption eines Kunstwerkes
sind Kunst-Laien oft viel empfänglicher als Kunstkenner, indes die
Beurteilung der Korrektheit, des Stils, der malerischen Durchführung
den Kenner verlangt. Der vollkommene Kenner freilich, wie er aber selten
zu finden, wird allen Seiten des Kunstwerks gleich gerecht.
Darin aber liegt ein großer Vorteil für die
hier geführte Untersuchung, dass wir keine ängstliche Auswahl
der Versuchssubjekte dabei zu treffen haben. Immer zwar wird es von Vorteil
sein, zu den Versuchen vorzugsweise sogenannte geschmackvolle Personen
zuzuziehen, d. i. welche eine Abweichung von dem Verhältnisse, das
sich schließlich aus der Gesamtheit der Urteile als das wohlgefälligste
herausstellt und das Normalverhältnis heißen kann, leicht und
fein in einer Verminderung des Wohlgefallens empfinden und befähigt
sind, feine ästhetische Unterschiede überhaupt leicht aufzufassen,
indem dann das Schwanken der Urteile geringer wird, und man mit einer geringern
Zahl von Subjekten ein verhältnismäßig sichres Resultat
erzielt. Da aber eine feste Grenze zwischen mehr und weniger geschmackvollen
Personen nicht zu ziehen und das Urteil über den Geschmack Andrer
selbst mit vom eignen Geschmacke abhängt, also objektiv unsicher bleibt,
so kommt uns die Betrachtung zu Statten, dass der minder gute Geschmack
eben sowohl nach der einen als andern Seite von dem Verhältnisse,
was der bessere Geschmack vorzieht, abweicht, so dass man je nach dem mehr
oder minder guten Geschmack der Versuchssubjekte zwar das Maß der
Schwankungsgröße, wovon später, aber nicht den Wert, um
den es schwankt, verschieden zu finden erwarten darf.
Wir haben das ästhetische Maß bis jetzt
überhaupt bloß aus objektivem Gesichtspunkte betrachtet, aber
das Vorige führt uns darauf, ihm auch eine subjektive Bedeutung in
sofern beizulegen, als es Anhalt zur quantitativen Vergleichung des Geschmackes
verschiedener Subjekte selbst gibt.
Wir sprechen überhaupt von einem verschiedenen
Geschmack, sofern Verschiedenen Verschiedenes gefällt und mißfällt
oder auch nur in verschiedenem Grade gefällt und mißfällt.
Betrachten wir nun in Bezug auf die einfachsten Verhältnisse den Geschmack
als den Normalgeschmack, welcher das Normalverhältnis vorzieht, also
mit der überwiegenden Zahl der Stimmen Gebildeter übereinstimmt,
so werden wir den minder guten oder richtigen Geschmack in dieser Beziehung
nach der größeren oder geringeren Abweichung des von ihm vorgezogenen
Verhältnisses vom Normal-Verhältnisse beurteilen und schließen
können, dass wenn Jemand in Bezug auf die einfachsten Fälle keinen
guten oder richtigen Geschmack beweist, es um so weniger in komplizierteren
Fällen der Fall sein wird, wogegen wenn sich sein Geschmack bei jenen
bewährt, zwar noch keine Gewißheit, aber eine günstige
Voraussetzung auch für letztere vorhanden sein wird. Hiernach lassen
sich einfache Rechtecke, Kreuze usw. oder die einfachsten Anwendungen solcher
Formen als Probeobjekte für den Geschmack aufstellen. Wer in meinen
Versuchen weit von dem Normalwert des Rechteckes, den Normalverhältnissen
des Kreuzes abweicht, erweckt mir stets den Verdacht keines guten Geschmackes
in rein ästhetischen Dingen überhaupt. Freilich bedarf die Beurteilung
hiernach großer Vorsicht, auch könnte ein Geschmack in direkter
Beziehung gut, in Betreff assoziativer Mitbestimmungen schlecht sein; und
jedenfalls ist bei Beurteilung des Geschmackes eines Einzelnen auf ein
einzelnes Urteil desselben wegen möglicher zufälliger Mitbestimmung
dabei nicht viel zu geben. Auch würden die angeführten Methoden
zwar zur Prüfung beizubehalten, doch anders zu disponieren sein; ich
habe sie aber nach dieser Seite bisher überhaupt nicht ausgebildet.
Außer der im vorigen Sinne erstandenen Güte
oder Richtigkeit des Geschmackes gilt es die Sicherheit oder Unsicherheit
desselben zu beurteilen. Wir sprechen bei einer einzelnen Person von einer
größeren oder geringeren Unsicherheit des Geschmacks, je nachdem
sie bei der Vorzugswahl zwischen verschiedenen ästhetisch zu vergleichenden
Verhältnissen oder überhaupt Objekten mehr oder weniger über
den Vorzug schwankt und sich bei Wiederholung des Urteiles zu verschiedenen
Zeiten, nachdem die Erinnerung an das früher gefällte Urteil
erloschen ist, mehr oder weniger verschieden entscheidet; bei einer Klasse
von Personen, je nachdem die Vorzugsurteile der Einzelnen bezüglich
der zu vergleichenden Objekte mehr oder weniger variieren. Um auch für
den Grad dieser Unsicherheit einen Maßstab zu haben, kann man aus
den Einzelnwerten v, wo zwischen das Schwanken stattgefunden hat,
das Mittel ziehen, die Abweichungen der Einzelwerte v von diesem
Mittelwerte bestimmen, und das Mittel dieser Abweichungen als Maßstab
der Unsicherheit oder Schwankungsgröße des Geschmacks nehmen.
Wo das Schwanken zwischen vielen Werten v stattgefunden hat,
kann man sich auch an die Bestimmung zweier Grenzen halten, die ich kurz
die Kerngrenzen nennen will. Hierzu ordnet man die erhaltenen Werte
v nach ihrer Größe, und zählt von den Enden der
Reihe, herein auf jeder Seite ein Vierteil der Werte ab, so dass in der
Mitte die gesamte Hälfte der Werte als Kern bleibt. In je stärkerm
Verhältnisse beide Grenzwerte des Kerns von einander abweichen, desto
größer ist das Schwanken. Nach den hierbei als gültig anzusehenden
Wahrscheinlichkeitsgesetzen stehen beide Maße bei großer Zahl
der v in prinzipieller Abhängigkeit von einander, das erste
aber ist sichrer, das zweite weniger umständlich zu gewinnen.
Dabei ist zu bemerken, dass diese Weise die Schwankungsgröße
des Geschmacks zu messen, keine prinzipiell geforderte ist, sondern nur
überhaupt den Zweck erfüllt, Gradationen der Schwankung nach
einem konsequenten Prinzip zu vergleichen. Insofern aber die Rech-nungen
mit den v fast alle logarithmisch zu führen sind, kann man
denselben Zweck noch einfacher und vielleicht angemessener dadurch erreichen,
dass man statt der im Sinne der folgenden Einschaltung zu verstehenden
mittleren Abweichung der Werte v von ihrem Mittel, die arithmetisch
mittlere Abweichung der log v vom Mittel dieser Logarithmen13)
oder den arithmetischen Unterschied zwischen den Logarithmen der Kerngrenzen
als Maßstab der Schwankungsgröße einführt, was sich
später durch den Gebrauch dieses Maßes erläutern wird.
13) Positive und negative Abweichungen dabei ohne Rücksicht
auf das Vorzeichen zusammengezählt.
Wenn im Vorigen und
Folgenden von Abweichungen oder Abständen zwischen Verhältnissen
so wie von Mittelwerten zwischen Verhältnissen die Rede ist, so können
darunter nicht arithmetische Abweichungen noch arithmetische Mittelwerte
im gewöhnlichen Sinne verstanden sein, welche, wie unten zu zeigen,
nach der gleichmöglichen Aufstellung der Verhältnisse in der
Form 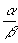 oder
oder 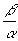 zu zweideutigen Resultaten führen, sondern nur Verhältnisabweichungen,
Verhältnismittelwerte, welche dieser Zweideutigkeit enthoben sind;
worüber hier Folgendes zu sagen. Der Kürze halber bezeichnen
wir dabei jedes einzelne Verhältnis so wie es als Dezimalzahl erscheint,
mit einem einfachen Buchstaben.
zu zweideutigen Resultaten führen, sondern nur Verhältnisabweichungen,
Verhältnismittelwerte, welche dieser Zweideutigkeit enthoben sind;
worüber hier Folgendes zu sagen. Der Kürze halber bezeichnen
wir dabei jedes einzelne Verhältnis so wie es als Dezimalzahl erscheint,
mit einem einfachen Buchstaben.
Man erhält
eine Verhältnisabweichung, oder für uns Abweichung schlechthin,
zwischen zwei Verhältnissen a, b nicht dadurch, dass
man eines beider Verhältnisse arithmetisch vorn andern abzieht, also
nicht als a - b oder b - a, sondern dadurch, dass man angibt,
in welchem Verhältnisse das eine vom andern überstiegen oder
unterstiegen wird, also selbst als Verhältnis zwischen den Verhältnissen
a, b, d. i. als 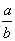 oder
oder 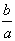 ,
womit sich die arithmetische Operation für Gewinnung der Verhältnisabweichung
von a, b auf die Logarithmen von a, b überträgt,
sofern
,
womit sich die arithmetische Operation für Gewinnung der Verhältnisabweichung
von a, b auf die Logarithmen von a, b überträgt,
sofern 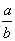 gleich der Zahl zu log a - log b ist, entsprechend mit
gleich der Zahl zu log a - log b ist, entsprechend mit 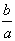 .
Den Wert log a - log b, also die arithmetische Abweichung
zwischen log a und log b nennen wir auch die logarithmische
Abweichung des Verhältnisses a vom Verhältnisse b.
Konsequent hängt hiermit zusammen, dass der halbe Abstand oder halbe
Unterschied des a vom b, in dem von uns festzuhaltenden Sinne
als Verhältnisunterschied, nicht
.
Den Wert log a - log b, also die arithmetische Abweichung
zwischen log a und log b nennen wir auch die logarithmische
Abweichung des Verhältnisses a vom Verhältnisse b.
Konsequent hängt hiermit zusammen, dass der halbe Abstand oder halbe
Unterschied des a vom b, in dem von uns festzuhaltenden Sinne
als Verhältnisunterschied, nicht 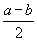 ,
sondern die Zahl zu
,
sondern die Zahl zu 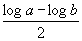 ,
d. i.
,
d. i. 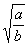 ,
entsprechend der doppelte Abstand die Zahl zu 2 (log a - log b)
d i.
,
entsprechend der doppelte Abstand die Zahl zu 2 (log a - log b)
d i. 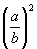 ist;
und wenn von einer Reihe äquidistanter Verhältnisse a,
b, c ... die Rede sein wird, so werden es nicht solche sein,
deren arithmetische, sondern deren logarithmische Differenzen gleich sind,
d. h. welche eine geometrische Reihe bilden, deren Exponent durch den Abstand
derselben in unserem Sinne gegeben ist.
ist;
und wenn von einer Reihe äquidistanter Verhältnisse a,
b, c ... die Rede sein wird, so werden es nicht solche sein,
deren arithmetische, sondern deren logarithmische Differenzen gleich sind,
d. h. welche eine geometrische Reihe bilden, deren Exponent durch den Abstand
derselben in unserem Sinne gegeben ist.
Eben so trägt
sich bei Mittelziehungen aus Verhältnissen a, b, c...
die arithmetische Operation von a, b, c ... auf die
Logarithmen von a, b, c. ... über, um das Verhältnismittel
oder sog. geometrische Mittel, um was es hier zu tun sein wird, als Zahl
dazu zu erhalten; wonach also das Mittel aus m Verhältnissen
a, b, c... nicht 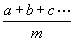 ,
sondern die Zahl zu dem Werte
,
sondern die Zahl zu dem Werte 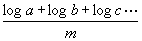 den
wir das logarithmische Mittel der Werte a, b, c ...
nennen, ist, d. i.
den
wir das logarithmische Mittel der Werte a, b, c ...
nennen, ist, d. i. 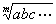 .
.
Auch Interpolationen
zwischen Verhältnissen können nach den gewöhnlichen, für
arithmetische Differenzen geltenden, Regeln nur zwischen den Logarithmen
der Verhältnisse vorgenommen und das Gauss’sche Gesetz zufälliger
Abweichungen als auf arithmetische Abweichungen bezüglich, nur an
den arithmetischen Abweichungen der Werte log v von ihrem arithmetischen
Mittel geprüft werden.
Zumeist genügt
es für den Zweck unserer Untersuchungen, bei den logarithmischen Resultaten
stehen zu bleiben, ohne auf die Zahlen dazu zurückzugehn, wie u. a.
bei dem vorigen Maße der Unsicherheit des Geschmackes.
Oben ward bemerkt,
dass die Anwendung arithmetischer Differenzen zwischen Verhältnissen
und arithmetischer Mittelwerte aus Verhältnissen auf Zweideutigkeiten
führe, welche ihren Gebrauch für uns ausschließen. In der
Tat, sei beispielsweise der arithmetische Unterschied so wie das arithmetische
Mittel zwischen den Dimensionsverhältnissen zweier Rechtecke zu bestimmen,
bei deren einem die kleinre Seite 1, die größre 2, bei dem andern
die kleinre 2, die größre 3 mißt, also, wenn wir die kleinre
Seite zum Zähler erheben, die arithmetische Differenz und das arithmetische
Mittel zwischen 1/2 und 2/3,
so ist die erste 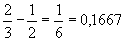 ,
die zweite
,
die zweite 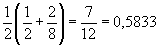 .
Es ist aber kein Grund, warum man den Ansatz obiger Dimensionsverhältnisse
nicht eben so gut in der umgekehrten Form
.
Es ist aber kein Grund, warum man den Ansatz obiger Dimensionsverhältnisse
nicht eben so gut in der umgekehrten Form 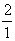 und
und 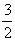 machen
sollte, da es willkürlich ist, ob man die größre oder kleinre
Dimension als Zähler und die andre als Nenner betrachtet. Soll nun
keine Zweideutigkeit entstehn, so muß das Resultat der umgekehrten
Aufstellung durch seine Umkehrung zum ersten Resultat zurückführen.
Dies ist bei arithmetischer Differenz und arithmetischem Mittel nicht der
Fall. Denn der arithmetische Unterschied zwischen
machen
sollte, da es willkürlich ist, ob man die größre oder kleinre
Dimension als Zähler und die andre als Nenner betrachtet. Soll nun
keine Zweideutigkeit entstehn, so muß das Resultat der umgekehrten
Aufstellung durch seine Umkehrung zum ersten Resultat zurückführen.
Dies ist bei arithmetischer Differenz und arithmetischem Mittel nicht der
Fall. Denn der arithmetische Unterschied zwischen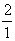 und
und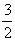 ist
ist 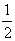 ,
und das arithmetische Mittel
,
und das arithmetische Mittel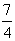 ;
aber 2 stimmt nicht mit
;
aber 2 stimmt nicht mit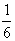 und
und 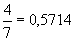 nicht mit
nicht mit 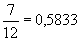 .
Bekanntlich nennt man den Wert, der durch Umkehr des nach der zweiten Aufstellungsweise
erhaltenen arithmetischen Mittels hervorgeht, das harmonische Mittel zu
dem nach der ersten Aufstellungsweise erhaltenen. Beide müßten
gleich sein, sollte das arithmetische Mittel für uns brauchbar sein,
sind es aber nicht. Hiergegen sind der Verhältnisunterschied und das
Verhältnismittel, im obigen Sinne verstanden, von dieser Zweideutigkeit
frei; indem danach das Resultat der umgekehrten Verhältnisse durch
seine Umkehr wieder zum ersten Resultat zurückführt.
.
Bekanntlich nennt man den Wert, der durch Umkehr des nach der zweiten Aufstellungsweise
erhaltenen arithmetischen Mittels hervorgeht, das harmonische Mittel zu
dem nach der ersten Aufstellungsweise erhaltenen. Beide müßten
gleich sein, sollte das arithmetische Mittel für uns brauchbar sein,
sind es aber nicht. Hiergegen sind der Verhältnisunterschied und das
Verhältnismittel, im obigen Sinne verstanden, von dieser Zweideutigkeit
frei; indem danach das Resultat der umgekehrten Verhältnisse durch
seine Umkehr wieder zum ersten Resultat zurückführt.
Nicht nur aus diesem
Grunde wird die verhältnismäßige Bestimmung der Differenzen
und Mittelwerte von Verhältnissen der arithmetischen vorzuziehen sein,
sondern auch weil es an sich rationeller, so zu sagen begrifflich commensurabler
erscheint, Verhältnisse nach Verhältnissen zu einander als nach
arithmetischen Differenzen zu vergleichen, anwachsen und sich vermindern
zu lassen.
Dazu noch Folgendes:
wenn es bloß das Mittel aus zwei Verhältnissen zu ziehen gilt,
so ist das Verhältnismittel von beiden, wie weit sie immer von einander
abweichen mögen, zugleich das Verhältnismittel zwischen dem arithmetischen
Mittel nach der einen Aufstellung und dem aus der andern Aufstellung abgeleiteten
harmonischen Mittel14),
kann also gewissermaßen beide, welche arithmetisch gleiche Berechtigung
haben, vertreten; ja approximativ gilt dasselbe auch bei Mittelziehung
aus mehreren Verhältnissen, so lange sie nicht zu weit von einander
abweichen.
14) Der, vielleicht schon irgendwo gegebene, Beweis
davon ist jedenfalls so leicht zu führen, dass ich glaube ihn übergehen
zu können.
Außer dem wohlgefälligsten Werte eines der
Variation unterliegenden Verhältnisses gibt es noch andre ästhetisch
bedeutsame Werte, die sich in Verbindung damit durch unsre Methoden bestimmen
und hinsichtlich ihres Verhältnisses zum wohlgefälligsten Werte
untersuchen lassen, woran bei der großen Unbestimmtheit und Oberflächlichkeit.,
welcher dies Feld der Untersuchung seither unterlegen hat, bis jetzt noch
niemand gedacht hat. Ehe wir aber darauf eingehen, noch folgende Bemerkung
hinsichtlich des wohlgefälligsten Wertes selbst.
Nach unsrer Begriffsbestimmung ist der wohlgefälligste
Wert eines der Variation unterliegenden Verhältnisses der, auf welchen,
– vorausgesetzt, dass er unter vergleichbaren Umständen gegen alle
andern gehalten wird – die meisten Vorzugsstimmen fallen oder um welchen
sich die Vorzugsstimmen am dichtesten zusammendrängen. Letztres aber
ist so zu verstehen. Es kann sein, dass nach erster Bestimmungsweise das
allerwohlgefälligste Verhältnis unter den Werten v, welche
die eine oder andre Methode liefert, gar nicht genau und sicher zu finden
ist, sei es, dass dies Verhältnis (bei erster Methode) gar nicht mit
vorgelegt ist, sei es, dass es (bei den andern Methoden) wegen beschränkter
Zahl der Versuche – von denen streng genommen eine unendliche Zahl erforderlich
wäre, um der Bevorzugung jedes möglichen v mit zugehörigem
z Raum zu geben – nicht genau mit dem größten z
der Verteilungstabelle getroffen ist, oder sich, (wie das gewöhnlich
ist,) mehr oder weniger unter größern oder kleinern Unregelmäßigkeiten
derselben versteckt. Dann aber wird es doch immer ein größeres
oder kleineres (logarithmisch abzumessendes) Intervall von Werten v
der Verteilungstabelle geben, auf welches mehr Vorzugsstimmen fallen, als
auf irgend ein andres Intervall gleicher Größe, oder worin sie
sich nach unserm kurzen Ausdruck am dichtesten zusammendrängen, und
in diesem Intervalle, was wir das dichteste nennen, wird man den wohlgefälligsten
Wert mit dem größtmöglichen z jedenfalls zu suchen
haben; daher wir ihn nach dieser Bestimmungsweise zum Vergleiche mit andern
alsbald zu besprechenden Werten auch wohl den dichtesten nennen
und mit D bezeichnen. Als ein je kleineres Intervall wir
nach Maßgabe der Vollkommenheit und Vollständigkeit der Versuche
das dichteste bestimmen können, desto genauer wird der wohlgefälligste
Wert als dichtester unmittelbar bestimmt sein, indem er jedenfalls zwischen
den Grenzen des dichtesten Intervalles liegen muß. Die rohe Bestimmung
eines nicht zu großen Intervalles, worin man ihn hiernach zu suchen
hat, ist bei hinreichender Zahl der Werte v und angemessener Anordnung
der Versuche schon ohne Rechnung möglich; die genauere Bestimmung
desselben (als eines zwischen unendlich nahen Grenzen liegenden Wertes)
aus dem Gange, welchen die Werte z in der Verteilungstabelle der
v um den dichtesten Wert herum nehmen, aber bedarf einer, übrigens
nicht schwierigen, Rechnungshilfe, wovon im folgenden Teile die Rede sein
wird. Jedenfalls ist die Bestimmung des so zu sagen idealen v, um
welches sich die Werte am dichtesten zusammendrängen, ausführbar;
die Genauigkeit dieser Bestimmung wächst aber mit der Zahl der Werte
v, die dazu in Rechnung genommen wird, und nimmt mit wachsender
Schwankungsgröße ab. Aus wenigen Werten ist überhaupt keine
genaue Bestimmung desselben zu gewinnen.
Es ist nun nicht selbstverständlich, dass der
dichteste, also wohlgefälligste Wert D eben so viel
größere Werte v über sich als kleinere unter sich
hat oder die Gesamtheit aller, nach ihrer Größe geordneten Werte
v der Zahl nach mitten durch teilt. Nennen wir überhaupt den
Wert, der diese Bedingung erfüllt, die Wertmitte oder den Zentralwert,
und bezeichnen ihn mit C. Eben so wenig ist selbstverständlich,
dass der dichteste Wert in gleichem zusammengesetzten Verhältnisse
der Größe nach von den andern Werten v überschritten
und unterschritten wird, d. i. dass er mit dem Verhältnismittel
oder sog. geometrischen Mittel zusammenfallt15),
was wir mit G bezeichnen und was dadurch erhalten wird, dass
man aus dem Produkte aller v, deren Zahl m sei, die m-te
Wurzel zieht, oder was auf dasselbe herauskommt, die Summe der Logarithmen
der v mit m dividiert und zum Quotienten die Zahl sucht.
Die Bestimmung der Werte C, G und die Frage,
ob sie mit D und miteinander koinzidieren, spielt in unserm
Untersuchungsfelde eine wichtige Rolle.
15) Dass das arithmetische Mittel der v außer Beachtung fällt,
geht aus der obigen Einschaltung hervor.
Wo D zugleich mit C und
G in so weit koinzidiert, dass man den kleinen Unterschied,
der übrig bleibt, als von unausgeglichenen Zufälligkeiten nicht
hinreichend vervielfältigter Versuche abhängig betrachten kann,
läßt sich von einer wesentlichen Symmetrie der Wohlgefälligkeitskurve
oder Verteilung der Werte v bezüglich D sprechen;
indem an der Koinzidenz von D mit C die gleiche
Zahl, an der Koinzidenz mit G die durchschnittlich gleiche
Größe der Abweichungen von D nach beiden Seiten
hängt.
Im physikalischen und astronomischen Beobachtungsgebiete,
wo man mit Beobachtungswerten einer einzigen Größe zu tun hat,
und das mit M zu bezeichnende arithmetische Mittel derselben
an die Stelle von G tritt, nimmt man an, dass nur unwesentliche,
d. i. von nicht ausgeglichenen Zufälligkeiten abhängige Abweichungen
zwischen M, C, D vorkommen, und
man könnte geneigt sein, dies ohne Weiteres auf unser Beobachtungsfeld
unter Ersetzung von M durch G zu übertragen.
Indes abgesehen, dass hierzu keine Berechtigung a priori vorliegt, hat
mich auch eine ausgedehnte Untersuchung an einer großen Zahl von
natürlichen und artistischen Kollektivgegenständen mit zufällig
variierenden Dimensionen ihrer Einzelexemplare gelehrt, dass selbst bei
einfachen Maßen, als bloßen Längen oder Breiten
der Exemplare, eine wesentliche Koinzidenz von D, sei es
mit C, G oder M, nicht allgemein
besteht, ja wohl öfter nicht besteht als besteht, und dass sie eben
so wenig für Dimensionsverhältnisse derselben allgemein
besteht, also kann eine solche auch nicht als selbstverständlich im
Felde unserer Untersuchung vorausgesetzt werden.
Inzwischen scheinen meine bisherigen Versuche doch
zu dem Resultate zu führen, ohne dass ich dasselbe schon als ganz
sicher aussprechen möchte, dass bei Abhängigkeit der Werte v
von reiner direkter Wohlgefälligkeit mit bloß zufälligen
Mitbestimmungen in der Tat eine Symmetrie der Verteilung in vorigem Sinne
stattfindet, wogegen D durch feste Mitbestimmungen dieser
oder jener Art aus seiner Mittelstellung auch verrückt werden kann.
Jedenfalls aber kann ich nach meinen allgemeineren
Untersuchungen im Felde von Kollektivgegenständen, dem ich unser Versuchsfeld
in dieser Hinsicht untergeordnet gefunden habe, folgenden wichtigen Satz
mit Sicherheit aussprechen:
Wenn zwei von den Werten D, C, G,
sei es bezüglich einfacher Werte oder bezüglich Verhältnissen,
womit wir hier zu tun haben, wesentlich, d. h. insoweit koinzidieren, dass
der übrig bleibende Unterschied dazwischen nur als von unausgeglichenen
Zufälligkeiten wegen zu geringer Zahl der Bestimmungen abhängig
angesehen werden kann, so findet auch eine entsprechende Koinzidenz mit
dem dritten statt; wogegen, wenn zwei davon so stark oder bei wiederholten
Bestimmungen so gesetzlich in bestimmter Richtung von einander abweichen,
dass man die Abweichung nicht als zufällig ansehen kann, auch der
dritte wesentlich von ihnen abweicht, und zwar ganz gesetzlich so, dass
der Zentralwert C zwischen dem Verhältnismittelwert G
und dichtesten Wert D liegt, wofür sich unter einer gewissen
allgemeinen Voraussetzung, die sich durch anderweite Resultate der Untersuchung
bestätigt findet, auch ein allgemeiner theoretischer Grund anführen
läßt, was aber näher zu besprechen und zu belegen hier
nicht der Ort ist. Genug, die Kenntnis dieser Verhältnisse ist, abgesehen
von ihrem allgemeinen theoretischen Interesse, hier für uns insofern
von praktischem Vorteil, als man danach in Fällen, wo man G
mit C wesentlich koinzidierend findet, die direkte Bestimmung
von D aus dem Gange der Werte durch die sichrere von G
oder minder umständliche von C ersetzen kann, und wo
G mit C nicht wesentlich koinzidiert, die Richtung,
in welcher D von C abliegt, danach bestimmen
kann.
Außer den vorigen Werten D, C, G
ist aus nachher anzugebendem Grunde nützlich, noch einen Wert zu berücksichtigen,
den ich den summarischen Mittelwert nenne und mit S
bezeichne, dadurch zu erhalten, dass man das arithmetische Mittel aller
Zähler der v, mit dem arithmetischen Mittel aller Nenner, oder
was auf dasselbe herauskommt, die Summe aller Zähler mit der Summe
aller Nenner dividiert16), wobei vorausgesetzt
ist, dass Zähler und Nenner alle nach wirklichen absoluten Maßen,
nicht teilweis reduziert gegeneinander, aufgeführt sind. Im Allgemeinen
fasse ich die Werte D, C, G, S als Hauptwerte zusammen.
16) Der Wert, welchen Zeising in dem Beispiele
S. 19 als Mittelwert aufführt, ist ein solcher summarischer Wert.
Das summarische Mittel kann vom Verhältnismittel
oder unserm Mittel schlechthin nicht unerheblich abweichen, wenn man willkürliche
Bruchwerte zum einen oder andern Mittel kombiniert. So ist das summarische
Mittel von 1/2, 2/3, 3/5
gleich 6/9 = 0,6666..., hingegen das Verhältnismittel 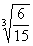 = 0,7368 ... Aber im Felde unsrer Untersuchung findet man im Allgemeinen
nur einen geringen, oft verschwindenden Unterschied zwischen beiden.
= 0,7368 ... Aber im Felde unsrer Untersuchung findet man im Allgemeinen
nur einen geringen, oft verschwindenden Unterschied zwischen beiden.
Des Näheren kommen überhaupt folgende
Verhältnisse des summarischen Mittels hier in Betracht.
Mögen Zähler und Nenner eines Verhältnisses
v kurz dessen Komponenten heißen, so haben auf den Wert von
S die Verhältnisse v mit größern Komponenten
einen größeren Einfluß, als solche mit kleinern Komponenten.
Denn seien z. B. 1/2 und 99/100
zwei Werte v, so wird im summarischen Mittel l gegen 99 und 2 gegen
100 merklich verschwinden, und sein Wert 100/102
= 0,9804 fast dasselbe Resultat geben, als wenn 1/2
gar nicht mit zugezogen wäre, wogegen in das Verhältnismittel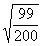 =
0,7036 beide Werte v rücksichtslos auf die absolute Größe
ihrer Komponenten mit gleichem Gewicht eingehen. Dies kann von vornherein
in allen Fällen, wo der Wert v in Abhängigkeit von der
absoluten Größe seiner Komponenten variiert, man aber keinen
Grund hat, auf Verhältnisse zwischen großen Komponenten bei
der Wohlgefälligkeits-Bestimmung mehr Gewicht zu legen, als aus kleinen,
als Vorteil des Verhältnismittels vor dem summarischen Mittel gelten.
=
0,7036 beide Werte v rücksichtslos auf die absolute Größe
ihrer Komponenten mit gleichem Gewicht eingehen. Dies kann von vornherein
in allen Fällen, wo der Wert v in Abhängigkeit von der
absoluten Größe seiner Komponenten variiert, man aber keinen
Grund hat, auf Verhältnisse zwischen großen Komponenten bei
der Wohlgefälligkeits-Bestimmung mehr Gewicht zu legen, als aus kleinen,
als Vorteil des Verhältnismittels vor dem summarischen Mittel gelten.
2) Das summarische Mittel stimmt mit dem
Verhältnismittel notwendig ganz überein, wenn bei beliebiger
Variation des absoluten Wertes von Zähler und Nenner doch das Verhältnis
beider konstant bleibt, oder weicht nur durch unausgeglichene Zufälligkeiten
davon ab, wenn das Verhältnis unabhängig von der Größe
seiner (Komponenten nach den Gesetzen des Zufalls variiert. Hingegen fällt
S gesetzlich größer oder kleiner aus als G,
je nachdem das Verhältnis mit wachsender Größe seiner beiden
Komponenten (oder nur eines derselben, wenn der andre konstant bleibt)
wächst oder abnimmt, wie man an willkürlichen Zahlenbeispielen
konstatieren kann17)
17) Einen allgemeinen Beweis dafür, den ich Prof.
Scheibner verdanke, werde ich nachträglich entweder im folgenden
Teile oder einer spätern Abhandlung über Kollektivgegenstände
mitteilen.
Hiernach aber gewinnt die Bestimmung des summarischen
Mittels aus doppeltem Gesichtspunkte ein Interesse und selbst eine Wichtigkeit
für uns. Erstens ist es leichter bestimmbar als jeder der andern vorgenannten
Hauptwerte, D, C, G, und kann bei fehlender oder nicht sehr
bedeutender Abhängigkeit des variierenden Verhältnisses von der
absoluten Größe des Zählers und Nenners (die man freilich
erst irgendwie geprüft haben muß) das Verhältnismittel,
und, wo dieses mit dem dichtesten Werte prinzipiell zusammenfällt,
diesen Wert ganz oder approximativ mit vertreten; zweitens gibt es uns
in seinem Verhältnisse zum Verhältnismittel unmittelbar, ohne
dass man eine Einzelrechnung deshalb anzustellen nötig hat, Aufschluß,
ob nach Maßgabe der absoluten Größe der Dimensionen oder
Abteilungen sich die Wohlgefälligkeit des Verhältnisses dazwischen
ändert18), was allerdings nicht bezüglich
der Wohlgefälligkeit abstrakter Verhältnisse an sich erwartet
werden kann, wohl aber unter dem Einfluß von Mitbestimmungen in den
Anwendungen nicht nur möglich ist, sondern auch sich als wirklich
vorkommend zeigen wird.
18) Nämlich wenn S > G
ist, so entsprechen die größern Werte von v mit ihrem
zugehörigen Wohlgefälligkeitsmaße z größern
Komponenten, hingegen, wenn S < G ist, kleineren
Komponenten, und reicht es also, um ein bestimmtes Wohlgefälligkeitsmaß
z zu erhalten , nicht hin, ein bestimmtes v überhaupt
zu haben, sondern es gehört dazu auch eine bestimmte Größe
der Komponenten.
In einem solchen Falle also wird man mit wachsender
oder abnehmender absoluter Größe der Komponenten das Verhältnis
derselben ändern müssen, um noch den größtmöglichen
Vorteil zu haben, und es wird dann einerseits darauf ankommen, darunter
den allerwohlgefälligsten Wert v mit der zugehörigen absoluten
Größe der Komponenten zu finden, andrerseits das Gesetz der
Abänderung von D nach der Größe der Komponenten.
Endlich gilt es noch, das Gesetz der Verteilung
der Werte v nach Zahl und Maß zu untersuchen, wozu die Untersuchung
der Symmetrie- oder Asymmetrieverhältnisse allerdings schon einen
Beitrag oder eine Unterlage bietet, ohne aber die Frage zu erschöpfen.
Auf den dichtesten Wert fällt seinem Begriffe nach die größte
Vorzugszahl; nach Maßgabe der Abweichung der Verhältnisse v
davon, sei es nach der einen oder der andern Seite, wird sich die relative
Vorzugszahl, die Größe des z, mindern, aber es fragt
sich, nach welchem Gesetze; wie hängt die relative Zahl der Bevorzugungen
mit der Größe der Abweichung vom dichtesten Werte zusammen?
Hierbei wird es insbesondere gelten, folgende Hypothese,
die sich auf Grund schon früher gepflogener Erörterungen darbietet,
zu prüfen. Man kann sich denken, dass der dichteste Wert als derjenige,
der die vorteilhaftesten Bedingungen des Gefallens in sich vereinigt, oder,
wie wir kurz sagen, ein Lustübergewicht an sich über alle andern
hervorruft, von Allen vorgezogen werden würde, wenn nicht unbestimmbare
zufällige subjektive oder objektive Mitbestimmungen bei den einzelnen
Versuchssubjekten obwalteten, wodurch mehr oder weniger große und
zahlreiche Abweichungen der Vorzugsurteile vom an sich wohlgefälligsten
Werte bedingt werden, ohne den Vorteil dieses Verhältnisses vor den
übrigen im Ganzen aufzuheben. Sofern nun diese Abweichungen
näher zugesehen darauf zu schreiben sind, dass das Lustübergewicht,
was das an sich wohlgefälligste Verhältnis19)
über die minder wohlgefälligen erweckt, durch die entgegenwirkenden
zufälligen Bedingungen überkompensiert wird, kann man die durch
den Erfolg selbst zu prüfende Hypothese aufstellen, dass jenes Übergewicht
ohne diese Gegenwirkungen entweder dem Verhältnisabstande selbst oder
dem zugehörigen logarithmischen Abstande des an sich wohlgefälligsten
Verhältnisses von den minder wohlgefälligen proportional sei,
wonach auch die gegenwirkenden zufälligen Bedingungen im Durchschnitt
proportional damit ansteigen müssen, um die Überkompensation
zu bewirken. Das werden sie aber um so seltener vermögen, je höher
sie dazu anzusteigen haben, indem in dieser Beziehung ein Wahrscheinlichkeitsgesetz
zwischen Zahl und Größe des Ansteigens besteht. Kurz, es muß
sich hiernach in der Verteilung der Werte v nach Maß und Zahl
das den Mathematikern wohlbekannte Gauss’sche Wahrscheinlichkeitsgesetz
zufälliger Abweichungen mit den Modifikationen wieder finden, welche
durch Anwendung auf Verhältniswerte v statt auf einfache Werte,
so wie auf unsymmetrische Verteilung, wo solche statt findet, geboten werden.
Auf die Erforschung dieser Modifikationen aber sind meine allgemeinen Untersuchungen
über Kollektivgegenstände nicht ohne Erfolg gerichtet gewesen,
und darf ich wenigstens für gewisse Fälle unseres jetzigen Untersuchungsfeldes
– denn zu einem allgemeinern Ausspruche fehlen mir noch hinreichend ausgedehnte
Unterlagen – die Bestätigung obiger Hypothese bezüglich logarithmischer
Abweichungen aussprechen. Den Ausspruch des Gesetzes selbst mit den darauf
bezüglichen Versuchen, so weit sie in unser Untersuchungsfeld gehören20),
werde ich im folgenden Teil geben, wohin ich auch Spezielles über
die Sicherheitsbestimmungen der Resultate verweise.
19) Oder auch unter festen assoziativen oder kombinatorischen Mitbedingungen
wohlgefälligste.
20) Im Übrigen habe ich auf die künftig zu veröffentlichenden
Untersuchungen über Kollektivgegenstände zu verweisen.
Um die betreffenden
Modifikationen, welche sich in der Anwendung des Gauss’schen Gesetzes auf
zufällig variierende Verhältniswerte, insbesondre bei asymmetrischer
Verteilung derselben, im Felde der Kollektivgegenstände nötig
machen, hier kurz zu resumieren, da sie auf unser jetziges Untersuchungsfeld
mit übergreifen, so sind es nach meiner allgemeinen Untersuchung folgende.
1) Die Anwendung
des Gesetzes ist, wie schon S. 56 erinnert, statt auf die Werte v
selbst auf deren Logarithmen zu machen; übrigens aber, im Falle symmetrischer
Verteilung der Werte in der bekannten Weise21)
vorzunehmen. Für Konstatierung der wesentlichen Symmetrie genügt
es nach S. 61. die wesentliche Koinzidenz zweier von den Werten D,
C, G oder ihren Logarithmen zu konstatieren.
21) Beispiel dazu: die Prüfung des Gesetzes durch
Bessel an Beobachtungsfehlern in s. Fundamentis Astronomiae p. 18.
2) Im Falle
wesentlich asymmetrischer Verteilung sind die Abweichungen der einzelnen
log v nicht vom Logarithmus des Verhältnismittels G,
sondern des aus den Logarithmen abgeleiteten dichtesten Wertes D
zu nehmen.
3) Die mittlere
Abweichung der log v von log D (sei es die einfache
oder aus den Quadraten der logar. Abweichungen zu gewinnende) ist für
jede Seite der Abweichungen besonders aus der Größe und Zahl
der Abweichungen dieser Seite abzuleiten, und hiernach auch die
Verteilung nach dem Gauss’schen Gesetze für jede Seite besonders vorzunehmen.
Diese Regeln gelten
übrigens im Felde der Kollektivgegenstände, so weit ich es bis
jetzt untersucht habe, nicht nur für variierende Verhältnisse
sondern auch für variierende einfache Werte, als namentlich
Dimensionen, wie ich mich sattsam an solchen, allerdings nicht häufig
vorkommenden Fällen überzeugt habe, die überhaupt eine Entscheidung
gestatten, d. i. wo die Variation der Einzelwerte im Verhältnis zur
Größe sei es des arithmetischen Mittels, oder des dichtesten
Wertes, so wie die Asymmetrie der Verteilung sehr beträchtlich ist.22)
Eins der auffälligsten Beispiele hiervon gewähren unter den artistischen
Gegenständen die Dimensionen von Galleriegemälden, die ich bei
Genrebildern, Landschaftsbildern und Stilleben (nach einer Reduktion der
Maße aus einer größern Anzahl von Galleriekatalogen auf
dieselbe Einheit) betreffs Höhe und Breite (im Lichten) besonders
in dieser Hinsicht untersucht habe23),
wo man mit der gewöhnlichen Anwendung des Gauss’schen Gesetzes so
wenig auskommt, dass ich dasselbe früherhin gar nicht für anwendbar
darauf hielt, wohl aber mit obigen Regeln seiner Anwendung auskommt. Dass
bei den hierher gehörigen Beispielen überhaupt (denn das vorige
Beispiel ist nicht das einzige, was mir in dieser Beziehung zu Gebote steht)
die Anwendung der Logarithmen der Einzelwerte in Berechnung der Verteilung
besser zur Erfahrung stimmt, als die Anwendung der Einzelwerte selbst,
beweist, dass diese Gegenstände (natürlich so weit ich sie untersucht
habe) nach einem kurzen (der Erläuterung wohl fähigen, doch dieselbe
ziemlich in sich tragenden) Ausdruck vielmehr nach Verhältnissen als
arithmetischen Differenzen variieren, worüber aber weitere Ausführungen
nicht hierher gehören würden.
22) Wo dies nicht der Fall ist, findet man ein merklich
gleich gutes Entsprechen mit der erfahrungsmäßigen Verteilung,
mag man die einfachen Werte selbst oder deren Logarithmen zur Berechnung
der Verteilung anwenden, und dabei (erstenfalls) die Abweichungen vom arithmetischen
Mittel oder (zweitenfalls) vom Logarithmus des dichtesten Wertes rechnen,
indem die Unterschiede im Erfolge beider Berechnungsweisen sich dann mit
der Unsicherheit der erfahrungsmäßigen Verteilung einer endlichen
Zahl von Werten zu sehr vermischen, um den Vorzug der einen vor der andern
Berechnungsweise durch Vergleich mit der Erfahrung sicher beurteilen zu
können, man müßte denn so viele Einzelwerte eines Kollektivgegenstandes
vor sich haben, als nicht leicht zu Gebote stehen.
23) Auch wurden dabei die Gemälde, bei welchen die
Breite größer als die Höhe ist, und bei welchen das Umgekehrte
stattfindet, gesondert.