Wir haben Empfindungssummen und Empfindungsunterschiede in Betracht zu ziehen Anlaß gefunden; es entsteht die Frage, ob nicht auch dem Begriffe eines Empfindungsproduktes Bedeutung beizulegen sei.

        ¹⁾ In Sachen S. 165 ff.

    Verständigen wir uns aber zuvor über den Begriff eines Produktes und nehmen, um uns nicht in unklare Abstraktionen zu verlieren, zum Anhalt ein bestimmtes Beispiel der Geometrie.

    Wenn wir ein Rechteck haben, dessen eine Seite 2, die andere 4 lang ist, diese Zahlen bezogen auf irgend eine Lineareinheit, so gibt das Produkt zwar nicht beider Seiten, denn ein solches gibt es nicht ²⁾, aber der Zahlen, wodurch ihre Länge gemessen wird, das Maß des Rechteckes bezüglich einer Flächeneinheit, welche mit der Lineareinheit in Beziehung steht.

    Nun fragt sich, ob auch einer Empfindung zwei in verschiedenem Sinne quantitativ bestimmbare Seiten oder Dimensionen zugeschrieben werden können, nach deren jeder sie für sich unabhängig von der anderen der Steigerung und Verminderung fähig ist, nach deren jeder sie durch eine der betreffenden Dimension homologe Einheit gemessen werden kann, und ob das Empfindungsresultat, was beide Seiten im Zusammentreffen geben, sein Maß eben so im Produkte der Maßzahlen finden kann, die beiden Seiten insbesondere zugehören, als das Rechteck im Produkte der Maßzahlen seiner Seiten.

    Zu Gunsten einer solchen Auffassung scheinen sich namentlich Stärke und Höhe eines Tones als Seiten desselben darzubieten. Und ich will zunächst das anführen, was sich in diesem Sinne geltend machen läßt.

    Sowohl Stärke als Höhe unterliegt dem Maße durch unsere Maßformel insbesondere. Nun macht allerdings die qualitative Verschiedenheit von Stärke und Höhe nötig, jede auf eine Einheit ihrer Art zu beziehen, und dies begründet einen Unterschied vom geometrischen Produkte, wo für beide auf einander senkrechte Seiten die gleiche Lineareinheit zu Grunde liegt. Aber da nicht die verschiedenen Qualitäten, sondern nur die darauf bezogenen abstrakten Maßzahlen zu multiplizieren sind, scheint mir darin um so weniger ein prinzipielles Hindernis zu liegen, als man durch die verschiedene Qualität von Stärke und Höhe des Schalls die verschiedene Richtung der Seiten eines Rechteckes vertreten halten kann. Ist die Einheit für beide Seiten der Empfindung einmal willkürlich gewählt, so wird jedenfalls nichts hindern, die darauf bezogenen Maßzahlen eben so mit einander zu multiplizieren, und die verschiedenen so gewonnenen Produkte mit einander zu vergleichen, als wenn man die Maßzahlen zweier auf einander rechtwinkligen Seiten multipliziert.

    Die wesentliche, die Hauptfrage ist nur, ob auch beide Seiten wirklich ein derartiges gemeinsames Empfindungsresultat geben, daß das Maß durch das Produkt der Maßzahlen der Seiten etwas bedeutet und dem Zusammenhange der Tatsachen entspricht. Ist dies der Fall, so kann kein mathematisches Bedenken mehr stattfinden.

    In der Tat scheint sich hiefür Manches anführen zu lassen.

    Es ist gewiß, daß der Totaleindruck eines hohen Tones durch seine Stärke vergrößert wird, und der Totaleindruck eines starken Tones in gewissem Sinne durch seine Höhe erhöht wird. Der Ton wird so zu sagen um so einschneidender, je höher er wird ³⁾. Auch verdient der Umstand Beachtung, daß es bekanntlich schwer ist, von der Gleichheit der Stärke verschiedener Töne bei verschiedener Höhe zu urteilen, indem das Urteil zwischen dem Maße des Gesamteindruckes und dem reinen Maße der Stärke zu schwanken scheint.

    Zur bestimmteren Unterscheidung nun bezeichnen wir folgends stets die Größe des Eindruckes, insofern sie bloß von Amplitude der Schwingungen abhängt, als Stärke, die Größe desselben, sofern sie bloß von Schwingungsdauer oder Schwingungszahl abhängt, als Höhe, die Größe des Eindruckes aber, sofern sie von beiden zugleich abhängt, als Intensität oder als Größe des Gesamteindruckes.

    Gesetzt hiernach, die Maße der empfundenen Schallstärke und Schallhöhe s und h seien für sich genommen respektiv

wo b die von der Amplitude abhängige physische Schallstärke, n die Schwingungszahl, t die Schwingungsdauer, b, n₁, t₁ die zugehörigen Schwellenwerte, k, k' Konstanten bedeuten, so würde das Maß der Intensität oder des Gesamteindruckes nach voriger Auffassung sein

oder, wenn wir die Schwellenwerte 1 setzen

    Sofern wir die physische Stärke eines Lichtes oder Schalls durch das Quadrat der Amplitude als gemessen ansehen, welche a heiße, wird sich a² für b in vorigen Gleichungen substituieren lassen, und, da log a² = 2 log a, der vorige Ausdruck übergehen in 2kk' log a log n, oder, indem wir auch 2kk' durch Wahl demgemäßer Einheiten gleich 1 annehmen, einfacher in log a log n.

    Jedoch halte ich die vorige Auffassung nicht nur nicht für bindend, sondern für nicht triftig, und nach alsbald zu erörternden Gründen als Maß des psychischen Gesamteindruckes oder der Intensität eines einfachen Tones statt der Form 2 kk' log  log die Form k log  für triftiger, wenn unter L die, von Amplitude und Schwingungszahl oder Schwingungsdauer zugleich abhängige, lebendige Kraft der Schwingungen und unter l deren Schwellenwert verstanden wird. Für Farben machen sich besondere Betrachtungen geltend, auf die ich unten komme.

    Nun kann L als gemessen angesehen werden durch das Quadrat des Produktes a n oder des Quotienten  , wozu die Schwellenwerte a₁n₁ und  seien; wonach der Ausdruck für das Maß der psychischen Gesamtstärke des Eindruckes, den ein einfacher Ton erzeugt, wäre

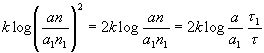
oder unter Wahl solcher Einheiten, wodurch 2k, a₁, n₁, t₁ gleich 1 werden

    So würde statt des vorhin erhaltenen Produktes der Logarithmen der Werte a, n, der Logarithmus des Produktes dieser Werte, oder, was dasselbe ist, die Summe der Logarithmen dieser Werte als Maß des psychischen Gesamteindruckes auftreten.

    Grailich in seinen sonst so schätzbaren Abhandlungen über das Zustandekommen zusammengesetzter Farben in den Sitzungsberichten der Wiener Akademie 1854. XII. S. 783. XIII. 201 setzt die lebendige Kraft der Lichtschwingungen, wovon der Empfindungseffekt abzuleiten, dem Quotienten aus der einfachen Schwingungsdauer in das Quadrat der Amplitude, oder, was dasselbe ist, dem Produkte aus der einfachen Schwingungszahl in das Quadrat der Amplitude, also dem Werte a²n proportional, indes Seebeck in seinen Abhandlungen über die Verhältnisse des Schalles (Poggend. Ann. LXII. 872. LXVIII. 461), eben so wie es hier geschieht, die lebendige Kraft der Schwingungen proportional n²a² setzt. Letzteres ist unstreitig triftiger ⁴⁾, und der Punkt, wo Grailich geirrt hat, leicht anzugeben.

wo t die Dauer einer Schwingung,  die Geschwindigkeit, t die Zeit ist, was durch Integration gibt

wenn man für  als Geschwindigkeit diejenige Funktion der Zeit t substituiert, welche in einer Schwingung statt hat, wenn a die Amplitude, p die Ludolfsche Zahl. Nun kann aber die lebendige Kraft einer Schwingung nicht maßgebend sein für die lebendige Kraft, welche durch Schwingungen während einer gegebenen Zeit entwickelt wird, um was es sich doch handelt, wenn die lebendige Kraft verschiedener Töne, Farben verglichen wird; sondern sie muß außerdem der Zahl der Schwingungen in dieser Zeit direkt, also mit t reziprok genommen werden, wodurch statt t vielmehr t² in den Nenner, oder das damit reziproke n² in den Zähler kommt.

    Es ist Schade, daß die mühsamen Rechnungen bezüglich der Intensitätswerte in Grailich’s Abhandlungen (Berichte Th. XIII. S. 230 ff.) dadurch ihre Triftigkeit verloren haben. Doch wird sein allgemeines Prinzip, die zusammengesetzten Farben zu erklären, dadurch nicht affiziert.

    Die Gründe, die letzte Auffassung der ersten vorzuziehen, sind folgende:

    Unstreitig haben wir Stärke und Höhe eines Tones nicht als etwas äußerlich Zusammengebrachtes anzusehen; sondern es liegt die Aufgabe in der Natur der Sache vor, den Eindruck der Stärke und Höhe im Zusammenhange aus den Grundbeziehungen der Empfindung zur Bewegung abzuleiten; und die einfachstmöglichen Voraussetzungen in dieser Beziehung werden uns im 32. Kapitel vielmehr auf einen Maßausdruck des Gesamteindruckes eines Tones von der Form log an als log a log n führen.

    Abgesehen hiervon spricht die Erfahrung direkt gegen die Form log a log n. Nach dieser Form gibt es einen festen Punkt der Stärke, bei welchem der Ton aufhört, hörbar zu sein, gleichviel, welche Höhe er habe, und einen festen Punkt der Höhe, wo er aufhört, gehört zu werden, gleichviel, welche Stärke er habe. Denn ist a oder n auf den Schwellenwert, der in der Form log a log n gleich 1 gesetzt ist, herabgekommen, so ist das Produkt log a log n in jedem Falle null, wie sich auch der andere Wert verhalte. Nicht so bei der Form log an. Hier kann Stärke durch Höhe und umgekehrt betreffs der Hörbarkeit vertreten werden; es besteht innerhalb der Grenzen der Höhe, die überhaupt nach der Einrichtung unseres Gehörorgans perzipiert zu werden vermögen, für jede andere Schwingungszahl n eine andere Amplitude a, bei welcher sie hörbar wird und umgekehrt. Der Ton wird hörbar, wenn das Produkt an den, hier kurz = 1 gesetzten, Schwellenwert a₁n₁ erreicht. Dies wird bei kleinem a sein, wenn n groß ist, und umgekehrt. So entspricht es aber der Erfahrung.

    In der Tat, tiefe Töne erfordern eine große Schwingungsamplitude, um noch hörbar zu sein, und hohe Töne können bei sehr geringer Stärke noch gehört werden.

    Diesen Umstand hat besonders Dove hervorgehoben, in Zusammenhang mit einer auf die Farben bezüglichen Tatsache, von welcher unten die Rede sein wird, die jedoch mindestens teilweise einen anderen Grund haben muß. Um hier zunächst bei dem, was sich im Tongebiete auf die Kompensation geringer Stärke durch vermehrte Höhe, oder geringer Höhe durch vermehrte Stärke bezieht, stehen zu bleiben, so erinnert Dove daran, "wie die Saiten des Contrabasses weiter schwingen müssen, als die der Violine; . .. . wie wir in höherem Tone sprechen, wenn wir ohne große Anstrengung gehört sein wollen; wie; wenn die tiefe, durch das Sprachrohr verstärkte, Stimme des Seemannes im Sturme verhallt, noch der schrillende Ton der Bootspfeife durch das Brausen der Wogen und das Geräusch des Windes hindurchdringt; und wie Savart mittelst der Speichensirene gezeigt hat, daß die Grenze der Wahrnehmbarkeit der Töne nach der Tiefe hin durch die Stärke der Töne erweitert werden kann."

    Auch folgender Umstand verträgt sich gar nicht mit der Form log a log n, indes er in die Form log a + log n wohl hineintritt.

    Wenn die Empfindung der Stärke oder Höhe ohne Rücksicht auf das andere Element allein sich ver-m-facht, so kann man dies nach jeder Voraussetzung durch m log a oder m log n darstellen. Nun tritt im Produkte log n log a der Faktor log n oder log a an die Stelle von m, und hiernach müßte man erwarten, falls anders mathematische Konsequenz bestehen soll, daß damit die Empfindung der Stärke im Verhältnisse von log n und die der Höhe im Verhältnisse log a wachse, also eine wechselseitige Steigerung der Stärke und Höhe eintrete, man also bei vermehrter Höhe eines Tones zugleich einen vermehrten Eindruck der Stärke, und bei vermehrter Stärke den Eindruck einer vergrößerten Höhe erhalte, was aber nicht der Fall ist. Bei der Form log a + log n tritt diese Schwierigkeit nicht ein.

    Allerdings steht der Form log an die Schwierigkeit entgegen, daß, wenn man mit der Vertiefung des Tones über eine gewisse Grenze geht, keine Verstärkung des Tones mehr hinreicht, ihn hörbar zu machen, und eben so gar zu hohe Töne nicht mehr hörbar sind, während doch nach der Form log an jede Verkleinerung von n durch eine Vergrößerung von a kompensiert wird, und der Eindruck des Tones mit wachsender Höhe ins Unbestimmte zunehmen müßte.

    Gewiß ist dies als eine Abweichung von der Gültigkeit der Formel log an an der unteren und oberen Grenze der Hörbarkeit der Töne anzusehen, wie wir aber schon sonst gewohnt sind, eine untere und obere Grenze für die Gültigkeit unserer Grundformeln zu finden, welche Grenzen doch voraussetzlich nur für die äußere, nicht für die innere Psychophysik bestehen, insofern die äußeren Reize nur innerhalb gewisser Grenzen, in denen sich der gewöhnliche Sinnesgebrauch hält, proportionale psychophysiscbe Bewegungen auslösen, auf welche die Grundformeln eigentlich zu beziehen sind, also auch nur innerhalb solcher Grenzen diese vertreten können.

    In der Tat ist der Gehörapparat des Menschen unstreitig bloß geeignet, Schwingungen innerhalb gewisser Grenzen der Höhe aufzunehmen und bis zu gewissen Grenzen der Stärke zu erzeugen, und die Unhörbarkeit noch so starker tiefer oder hoher Töne beruht hiernach nicht darauf, daß sehr langsame oder schnelle psychophysische Oszillationen selbst bei größter Amplitude unhörbar sind, sondern daß sie im Menschen gar nicht in erforderlicher Stärke zu Stande kommen, wenn schon äußere Schwingungen dazu da sind.

    Schon das Trommelfell mit seinen annektierten Teilen kann bei zu großer Höhe oder Tiefe die Dienste versagen ⁴⁾; ja durch ein von Wollaston angegebenes Mittel sogar künstlich taub gegen tiefe Töne gemacht werden ⁵⁾. Außerdem ist nicht unwahrscheinlich, daß die Nerventasten, die von den Tönen angeschlagen werden, oder akzessorischen Apparate, mittelst deren sie nach neueren Untersuchungen angeschlagen zu werden scheinen, nur bis zu einer gewissen Höhe reichen. In der Tat liegen viele Gründe vor, worauf ich im 33. Kapitel näher eingehe, zu vermuten, daß zur Apperzeption von Tönen verschiedener Höhe verschiedene Nervenfasern gehören.

    Nicht ohne Interesse ist folgende Bemerkung von Wollaston ^†):

    "From the numerous instances in which I have now witnessed the limit to acuteness of hearing, and from the distinct succession of steps that I might enumerate in the hearing of different friends, as the result of various trials that I have made among them, I am inclined to think, that at the limit of hearing, the interval of a single note between two sounds, may be sufficient to render the higher note inaudible, although the lower is heard distinctly."

Man kann bemerken, daß die Form log a + log n, oder, um die Schwellenwerte wieder mit einzuführen, log  + log  mit der, in der Summenformel sich darbietenden Form

log  + log  ganz übereinstimmt, welche stattfindet, wenn wir zwei Reizgrößen b, b ' auf zwei verschiedene Punkte mit verschiedenen Empfindlichkeiten wirken lassen. Die Bedeutung dieser Form verallgemeinert sich also dahin; daß nicht bloß das, was derselben Seite der Empfindung angehört, auf zwei verschiedenen Punkten, sondern auch das, was zwei verschiedenen Seiten angehört, auf demselben Punkte sich unter dieser Form verbinden. Und dies hat beidesfalls den übereinstimmenden Erfolg: daß, so wie die Reizgrößen auf zwei verschiedenen Punkten einer gesonderten Auffassung unterworfen werden können, indes sie doch in einer gemeinsamen Raumanschauung begriffen bleiben, so Stärke und Höhe auf demselben Punkte, indes sie in einer gemeinsamen Tonempfindung begriffen bleiben.

    Bei der übrigens stattfindenden gänzlichen Übereinstimmung der Form log+ log  mit der Form log  + log  ist jedoch der Unterschied nicht zu übersehen, daß in letzter Form b, b' unabhängig von einander sind, indes in erster a₁, und n₁ durch die Gleichung a₁n₁ = Konst. verknüpft sind. Dies führt mit sich, daß der empfundene Höhenunterschied der Töne durch ihre verschiedene Stärke eben so wenig abgeändert wird, als die Höhe selbst. Denn es sei der eine Ton log , der andere log , so ist a₁ zwar von a'₁ und n₁ von n'₁ verschieden, aber a'₁ n'₁ = a₁ n₁ und der gesamte Tonunterschied

    Ungeachtet ein tiefer schwacher und ein hoher starker Ton einen Maßausdruck von gleicher Größe haben können, so ist doch der qualitative Eindruck oder Charakter beider nach der Zusammensetzung dieses Maßausdruckes verschieden. Der erste erscheint uns verhältnismäßig ernst, würdig, schwer, breit, der zweite spitzig, dünn, schrillend.

    Die Triftigkeit der Form log an vorausgesetzt, so ist der Schwellenwert der Stärke eines Tones nur insoweit konstant, als die Höhe konstant ist, und der Schwellenwert der Höhe nur in soweit, als die Stärke konstant ist, und es steht, allgemein gesprochen, der Schwellenwert der Schwingungszahl, wovon die Höhe abhängt, im umgekehrten Verhältnisse der Amplitude der Schwingung, und umgekehrt der Schwellenwert der Amplitude der Schwingung im umgekehrten Verhältnisse der Schwingungszahl, im direkten der Schwingungsdauer.

    Wahrscheinlich bestehen in Betreff der Grenzen der Hörbarkeit der Töne große Verschiedenheiten zwischen verschiedenen Geschöpfen (wie dies Wollaston spezieller ausgeführt hat), indem jedes Geschöpf je nach seiner Lebensweise mit Aufnahmsorganen und Nerventasten für einen gewissen größeren oder kleineren, höheren oder niederen Teil der Tonskale versehen sein mag, wobei wir immer vorauszusetzen haben werden, daß schnellere Schwingungen und kleinere Amplituden zusammengehören. Wenn das, was für Tonschwingungen gilt, sich auf alle Schwingungen, von denen Empfindungen abhängen, verallgemeinern lassen sollte, so haben wir gewissermaßen schon in Auge und Ohre zwei so verschiedene Geschöpfe, da die Lichtschwingungen bei ungeheurer Kleinheit ungeheuer schnell, die Schallschwingungen bei viel größerer Langsamkeit viel größer sind, insofern es als wahrscheinlich gelten kann, daß dies Verhältnis der äußeren Schwingungen sich ins Innere übersetzt. Freilich kann, wie alsbald erörtert werden soll, die Form log an auf Farben keine direkte Anwendung finden, wenn wir die Abhängigkeit der Empfindung vom äußeren Farbenreiz danach messen wollen; doch ist damit die Möglichkeit noch nicht ausgeschlossen, daß, wenn uns eine letzte Analyse der inneren Schwingungsbewegungen, die der Lichtempfindung unterliegen, zu Gebote stände, die Maßform log an auch hier maßgebend sein würde.

    Man könnte sich Systeme denken, in welchen Bewegungen von so langer Periode als die Bewegung der Erde um die Sonne doch noch Empfindungsphänomene vermittelten; wenn zugleich die Amplitude entsprechend groß wäre; auch können wir nicht wissen, ob die Welt selbst nicht ein solches System ist. Nur wäre es nutzlos, solchen Möglichkeiten hier weiter nachzugehen.

    Das Vorige zusammengefaßt, so hängt die strenge Begründung der Form log an als Maßausdruck für die Intensität der Tonempfindung und die etwaige Übertragbarkeit dieser Form auf andere Empfindungen an zwei Bedingungen: 1) daß das Weber’sche Gesetz für Stärke und Höhe insbesondere gilt, wie es sich wirklich bei Tönen so gefunden hat; hieran hängt die logarithmische Form des Maßausdruckes und seine Zerlegbarkeit in zwei unabhängige Glieder; 2) daß die Intensität des Toneindruckes dieselbe bei gleichbleibender lebendiger Kraft a²n² und mithin gleichem Schwingungsprodukt an bleibe, mithin die Verringerung der Hörbarkeit bei verminderter Amplitude durch eine entsprechende Vermehrung der Schwingungszahl und umgekehrt die Verminderung der Hörbarkeit bei verminderter Schwingungszahl durch eine entsprechende Vermehrung der Amplitude kompensiert werden könne, was man ebenfalls bei Tönen in soweit als bestätigt ansehen kann, als man nach dem allgemeinen Ausfalle von Erfahrungen, wie solche (s. o.) angeführt wurden, gehen kann.

    Inzwischen reicht Letzteres freilich zu einer genauen Bewährung noch nicht hin, und in dieser Beziehung ist folgende Bemerkung wichtig. Sowohl die Gültigkeit des Weber’schen Gesetzes für Stärke und Höhe insbesondere, als die Kompensierbarkeit der Stärke durch Höhe und umgekehrt in Betreff der Hörbarkeit des Tones im Allgemeinen, soweit sie bis jetzt durch allgemeine und unbestimmte Erfahrungen konstatiert ist, würden sich ebensowohl mit Formen des Maßausdruckes von der Form log an² oder log a²n, als der Form log an vertragen. So daß durch Erfahrung noch nicht zwischen diesen verschiedenen Formen entschieden ist, und die Form log an nur wegen ihrer größeren Einfachheit und einfacheren Beziehung der Empfindungsgröße zur Größe der lebendigen Kraft so lange vorgreiflich zu bevorzugen sein dürfte, als eine direkte Entscheidung nicht vorliegt.

    Eine solche Entscheidung, ließe sie sich durch das Experiment gewinnen, wozu, wie ich unten zeige, nicht alle Aussicht fehlt, würde aber von äußerster Wichtigkeit sein. Aus den Erörterungen eines künftigen (des 32.) Kapitels geht nämlich hervor, daß die Form log an gefordert wird, wenn die Intensität der Empfindung von der Größe der Geschwindigkeiten, die Form log an² aber, wenn sie von der Größe der Geschwindigkeitsänderungen (Geschwindigkeiten zweiter Ordnung), die im Laufe einer Schwingung stattfinden; im Sinne der Maßformel abhängt, welches eine ganz fundamentale Frage für die Psychophysik ist, über die auf diese Weise entschieden werden könnte. Und ungeachtet ich beim bisherigen Mangel einer solchen Entscheidung die Form log an als die einfachere bevorzugt habe und demnächst bevorzugen werde, stelle ich es doch noch ganz dahin, ob dieser Vorzug sich bewähren wird ⁹⁾. Der Unterschied zwischen beiden Formen macht sich übrigens nicht sowohl in allgemeinen Folgerungen als den Verhältnissen der Maßwerte von Stärke und Höhe, an die sie sich knüpfen, geltend.

    Gesetzt, man läßt denselben Hammer immer aus derselben Höhe auf dieselbe horizontale Saite, aber bei verschiedener Spannung derselben, fallen, oder dasselbe Pendel immer bei Erhebung um denselben Elongationswinkel gegen dieselbe aber verschieden gespannte vertikale Saite schlagen, so wird sich die Saite immer mit gleicher lebendiger Kraft bewegen, aber je stärker sie gespannt wird, desto mehr wird a abnehmen, n zunehmen, d. i. sie wird in immer kleinerer Amplitude schwingen, indes sie zugleich eine immer größere Tonhöhe erlangt, Das Produkt a²n², mithin auch an wird gleich bleiben.

    Gilt nun der Maßausdruck log an, so wird auch der Ton immer bei derselben Fallhöhe hörbar zu werden anfangen und aufhören, wie man auch die Spannung der Saite abändere; oder, falls man den Versuch mit zwei gleichen aber verschieden gespannten Saiten und zwei dazu gehörigen gleich konstruierten Hämmern oder Pendeln bei gleicher Fallhöhe (unter Umkehr des Versuchs mit beiden) anstellt, was unstreitig den Vergleich erleichtern würde, der Ton beider bei derselben Entfernung des Hörenden anfangen und aufhören bemerklich zu werden.

    Ist hingegen die Form log an² triftig, so wird die Hörbarkeit durch Vergrößerung von n mehr zunehmen, als durch Vergrößerung von a.

    Sollte die Form log a²n gelten, was vorauszusetzen jedoch kein theoretischer Grund vorliegt, so würde das Umgekehrte gelten.

    Für den Augenblick bin ich nicht in der Lage, diesen Versuch genau genug mit den erforderlichen Abänderungen anzustellen, was mir vielleicht künftig möglich sein wird; wenn nicht inzwischen, wie ich wünsche, Andere sich desselben angenommen haben. Unstreitig würde sich noch mehr von demselben erwarten lassen, wenn nicht ein Umstand wäre, der seine entscheidende Kraft sehr beeinträchtigen muß. Sein Resultat würde einfach und unzweideutig sein, wenn der Gehörapparat jedes n gleich leicht aufnähme, d. h. der Amplitude der äußeren Schwingungen mit proportionaler Amplitude der inneren korrespondierte, aber nach den mitgeteilten Tatsachen ist dies nicht der Fall; und je mehr das n sich den Grenzen der Hörbarkeit nähert, desto mehr muß bei gleichbleibendem Werte an die Hörbarkeit abnehmen, selbst wenn die Form log an bezüglich der inneren Bewegungen richtig sein sollte, was zu untersuchen das Hauptinteresse ist. Es wird die Frage bleiben, inwiefern die etwa bemerkten Abänderungen in der Hörbarkeit verschieden hoher Töne bei gleicher lebendiger Kraft vielmehr davon abhängen, daß die Gleichheit der lebendigen Kraft der äußeren Schwingungen sich nicht ins Innere übertragt, oder davon, daß der innerlich gleichen lebendigen Kraft bei verschiedenem n und a keine gleiche Intensität der Empfindung zugehört. Inzwischen ließe sich doch vielleicht durch Kombination der Resultate von Versuchen 1) gegen die untere, 2) gegen die obere Grenze der Hörbarkeit, 3) um die Mitte zwischen beiden ein bindender Schluß ziehen; zumal nicht unwahrscheinlich eine derartige Accommodationsfähigkeit der Spannung des Trommelfelles stattfindet, daß die Perzeption verschieden hoher Töne innerhalb gewisser Grenzen gleich leicht erfolgt.

    Sollte jedoch der Versuch wegen nicht lösbarer Komplikation der Bedingungen kein hinreichend entscheidendes Resultat in Betreff der, die innere Psychophysik angehenden, Haupt-frage liefern, so würde es immerhin nützlich sein, sein zusammengesetztes Resultat für die äußere Psychophysik festgestellt zu haben.

    Mag nach Allem der Maßausdruck log an oder log an² sich als der triftigere erweisen, so läßt er sich doch nach den bisher vorliegenden allgemeinen Erfahrungen nur für das Gebiet der Töne, nicht der Farben in Anspruch nehmen. Denn für Farben besteht nach der schon Th. I. S. 175 gemachten Bemerkung das Weber’sche Gesetz nicht eben so wie für Tonhöhen, also schon die erste Bedingung der Form log an oder log an² trifft hier nicht zu; und es gibt eine Tatsache, wonach auch die zweite nicht zutrifft.

    Diese, wenn ich nicht irre, zuerst von Purkinje¹⁰⁾ bemerkte, von Dove¹¹⁾ seinerseits selbst-ständig aufgefundene und genauer verfolgte, von Grailich¹²⁾ gelegentlich konstatierte, von Helmholtz ^†) am schärfsten bestimmte und formulierte Tatsache, zufolge deren man in der Dämmerung das Blau länger als das Rot erkennt, was am Tage einen stärkeren Eindruck macht, wird von Letzterem in folgendem Satze oder Gesetze ausgesprochen. "Zwei farbige Lichtmengen, welche bei einer gewissen absoluten Lichtintensität gleich hell erscheinen, tun es im Allgemeinen nicht mehr, wenn die Lichtmengen beider verdoppelt oder halbiert werden. Und zwar wird im ersten Falle die minder brechbare der beiden Farben, im letzten die brechbarere die hellere werden."

    Man darf diese Tatsache nicht, wie es wohl geschehen ist, mit der Tatsache gleichgeltend halten, daß eine größere Schwingungszahl eine kleinere Amplitude für die Wahrnehmbarkeit kompensieren kann; denn während letztere, bei Tönen hinreichend konstatierte, Tatsache in die Form log an oder log an² hineintritt und dadurch gefordert wird, widerspricht die im Helmholtz’schen Satze enthaltene Tatsache, die bis jetzt bloß bei Farben, nicht bei Tönen konstatiert ist, dieser Form, wie jeder Form, welche eine gleiche Wahrnehmbarkeit an eine gleiche lebendige Kraft oder an die Gleichheit eines Produktes wie an² oder a²n knüpft. Denn wenn bei zwei Tönen oder Farben a²n² = a'²n'², mithin an = a'n' ist, so wird auch 2an = 2 a¢ n¢ bleiben müssen; und also weder die logarithmische noch irgend welche Funktion von a²n² oder an als Maßausdruck für die Intensität der Empfindung sich mit dem Helmholtz’schen Satze vertragen. Entsprechend bei Funktionen von an² oder a²n. Wenn also Blau bei Dämmerung das Rot überwiegt, so müßte es nach solcher Form des Maßausdruckes auch noch bei größter Tageshelligkeit dasselbe überwiegen; wogegen die Dove’schen Erfahrungen und der Helmholtz’sche Satz das Gegenteil besagen.

    Untersucht man, ob etwa die Form log a log n geeigneter wäre, den Helmholtz’schen Satz als Folgerung herzugeben, so zeigt sich, daß man vielmehr noch schlechter damit fahren würde; indem, wenn man bei zwei an Größe gleichen Intensitäten log a log n und log a' log n' die Amplitude a und a' in demselben Verhältnisse vergrößert, nicht nur keine Gleichheit der Intensitäten bleiben kann, sondern dem Helmholtz’schen Gesetze gerade entgegen die Farbe mit der größeren Schwingungszahl in Übergewicht kommen muß.

In der Tat gehen die Intensitäten log a log n und log a' log n' durch Multiplikation der Werte a und a' mit demselben Werte m über in

    Also kann man die unstreitig stattfindende Gemeinsamkeit der Tatsache für Farben und Töne, daß kleinere Schwingungszahlen eine größere Amplitude fordern, um wahrnehmbar zu sein, doch nicht mit einer Gemeinsamkeit des Helmholtz’schen Gesetzes für beide verwechseln, welche keineswegs damit gesetzt ist¹³⁾, und ich halte es für nicht unwahrscheinlich, daß das Helmholtz’sche Gesetz bei Farben mit so vielen anderen Abweichungen, welche die Verhältnisse der Farben von denen der Töne darbieten und welche ich im 33. Kapitel besonders zusammenstellen werde, zusammenhängt, und also nur für Farben, nicht für Töne gilt, in welcher Beziehung freilich direkte Versuche, in Verbindung mit dem oben vorgeschlagenen, noch sehr wünschenswert wären.

        ¹⁴⁾ Pogg. XCIV. 13.

    Hiernach bleiben zwei sehr wichtige Fragen übrig.

    Erstens. Es hat sich teils als gewiß, teils als wahrscheinlich gezeigt, daß die Farbenempfindungen nicht in gleicher Weise von den Schwingungszahlen abhängen, als die Tonempfindungen, denn sonst müßte sich für sie gleicherweise das Weber’sche Gesetz bestätigen. Was kann der Grund des Unterschiedes sein, nachdem sie doch faktisch überhaupt davon abhängen? Auf diese Frage gehe ich näher im 33. Kapitel ein, worin sich, wenn nichts schlechthin Gewisses; doch manches von vorwiegender Wahrscheinlichkeit über diesen Gegenstand wird sagen lassen.

    Zweitens. Nach den früheren Untersuchungen über Stärke und Höhe der Töne (Th. I. Kap. 9) hängt der Eindruck beider nach gleichem Gesetze, der der Stärke von der Amplitude, der der Höhe von der Zahl der Schwingungen ab, und hiernach schiene es, daß alle Verhältnisse sich für die Empfindung der Stärke und Höhe gleichstellen müßten. Aber so ist es doch nicht. Die Skala der Höhen trägt einen natürlichen Maßstab für das Gefühl in sich, welchen die Skala der Stärken nicht in sich trägt, und außer dem Eindrucke der Progression bei dem Aufsteigen in der Skala der Höhen haben wir auch den Eindruck einer Periodizität, den wir beim Aufsteigen in der Skala der Stärke nicht haben. Denn bei jedem Fortschritte um eine Oktave in der ersten Skala sagt uns das Gefühl zugleich, daß wir um ein Gleiches fortgeschritten und in gewissem Sinne zum früheren Eindrucke zurückgekehrt sind, wovon beim Fortschritte in der Skala der Stärken nichts Analoges stattfindet.

    Mit dem Gefühle für die Oktave hängt natürlicherweise das Gefühl für die Untereinteilungen der Oktave zusammen. Die Skala der Stärken ist eine für das Gefühl schlechthin unendliche, wovon es keine endlichen Verhältnisteile überhaupt gibt, wogegen das auf der Skala der Höhen abgegrenzte endliche Intervall der Oktave auch endliche Verhältnisteile zuläßt. Denken wir uns beide Skalen als Säulen, die ins Unendliche verlaufen. Aber auf der Säule der Höhen sind die Fuße abgeteilt und hiernach schätzen wir dann leicht die Zolle. Auf der Säule der Stärken ist nichts abgeteilt, und so haben wir auch keinen Anhalt, Unterabteilungen durch Schätzung zu bestimmen.

    Woher dieser Unterschied zwischen der Empfindungsskala der Stärken und Höhen der Töne bei gleicher mathematischer Repräsentation? womit man gleich die, in die vorige Frage mit hineintretende, Frage verbinden kann, woher der Unterschied, den die Töne in dieser Hinsicht von den Farben, die doch eben so wie sie an der Schwingungszahl hängen, darbieten? Denn die Farben bieten doch nichts dem musikalischen Eindrucke des Oktavenintervalls und seiner Unterabteilungen Analoges dar. Zwar scheint das Farbenspektrum durch Violet am brechbaren Ende eine Rückkehr zum Rot am mindest brechbaren Ende anzudeuten, worüber man Näheres im 33. Kapitel nachlesen mag; aber ein Maßgefühl der Zwischenintervalle zwischen Rot und Violet ist damit nicht im Geringsten gegeben; die Farben machen ihren charakteristischen Eindruck überhaupt unabhängig von ihrer Beziehung zu einander, und die Kontrastempfindungen, die in ihrer Beziehung begründet liegen, haben nichts gemein mit den Empfindungen der musikalischen Intervalle der Quinte, Quarte u. s. f.

    Zeigt sich nicht, kann man fragen, hier eine Unzulänglichkeit der Theorie?

    Meines Erachtens nicht eine Unzulänglichkeit insofern, als ob die bisherige Theorie irrig wäre, wohl aber eine Unvollständigkeit, sofern sie noch einer Ergänzung bedarf. Ehe ich nun diese zu geben versuche, will ich aber die sinnreiche graphische Konstruktion und Exposition mitteilen, wodurch Drobisch schon vorlängst den Gang des progressiven Aufsteigens zugleich mit der periodischen Wiederkehr der Toneindrücke beim Durchschreiten der Tonskala versinnlicht hat, eine Darstellung, die man gewiß nicht ohne Interesse hier wiederfinden wird¹⁵⁾.

    "Denkt man sich das Intervall 1 der Oktave mit dem Grundtone als den Umfang eines Kreises, dessen Halbmesser also = 0,15915 sein muß, so werden alle übrigen Intervalle Bogen dieses Kreises, deren zugehörige Mittelpunktswinkel sich leicht bestimmen lassen. Denn offenbar ist, wenn der dem Intervalle x entsprechende Winkel = w,

Hiernach ergeben sich für die dreizehn Hauptintervalle folgende Werte von w, denen wir unter w' die Werte beifügen, die den durch Zwölftel der Oktave ausgedrückten Intervallen der Tasteninstrumente entsprechen.

                                                                                                                   w            w'

        ¹⁶⁾ Auf diese bildliche Darstellung hat uns eine Stelle in Newton’s Optik (Lib. l. Pars II. Prop. VI) geleitet.

     "Diese Drehung des Halbmessers gibt jedoch von der Veränderung, welche der Ton erleidet, wenn er von dem Grundtone allmählich zur Oktave übergeht, nur ein unvollständiges Bild; denn die Oktave ist bei aller Verwandtschaft mit dem Grundtone doch ein von diesem unterscheidbarer Ton. Man sagt nun zwar, sie sei der Grundton in einer höheren Lage, ohne aber darüber eine deutliche Auskunft zu geben. Nahe genug liegt hier die Bemerkung, daß, da die Änderung der Töne eine allmähliche ist, diese höhere Lage nicht plötzlich, erst mit der Oktave, eintreten kann, sondern ein stetiger Übergang zu ihr stattfinden muss."

    "Wir erhalten hierüber eine völlig genügende Aufklärung, wenn wir der Gleichung y = 2^x, die den Zusammenhang zwischen der relativen Schwingungszahl y eines Tones und seinem Intervalle x mit dem Grundtone darstellt, eine angemessene geometrische Auslegung geben. Wie nämlich die Werte von x durch Bogen eines Kreises, so können die Werte von y durch gerade Linien dargestellt werden, die in den Endpunkten jener Bogen senkrecht auf der Ebene des Kreises stehen. Offenbar liegen dann diese die Werte von y darstellenden Geraden in der krummen Fläche eines Zylinders, der jenen Kreis zur Basis hat, ihre Endpunkte in einer sich um den Zylinder windenden logarithmischen Spirale. Da für x = 0, y = 1, so ist der Abstand des dem Grundtone entsprechenden Punktes dieser Spirale von der Basis des Zylinders = 1; und da für x = 1, y = 2, so ist der Abstand des der Oktave entsprechenden Punktes doppelt so groß. Jeder zwischenliegende Ton, für welchen immer 1 > x > 0 und 2 > y > 1, hat seinen entsprechenden Punkt in der Spirale. Hiernach stellen also x und y die Koordinaten einer logarithmischen Spirale auf der Fläche eines geraden Zylinders dar, und kann y als die absolute Höhe des Tones, x als seine Abweichung von der Richtung des Grundtones bezeichnet werden."

"Setzt man y - 1 = u, so drückt u die relative Höhe des durch die relative Schwingungszahl y gegebenen Tones in Bezug auf die Höhe seines Grundtones, oder kürzer die Erhebung des Tones über den Grundton aus; dann ist also

    Die Werte von u werden dargestellt durch die Abstände der Punkte der Spirale von der Ebene des Kreises, die parallel zu der Ebene der Basis durch den Punkt der Spirale gelegt wird, welcher dem Grundtone entspricht; oder x und y sind die Koordinaten der Spirale, welche sich auf diesen der Basis parallelen Schnitt des Zylinders beziehen....."

    "Nach dieser (durch Fig. 3 und deren Exposition im Originale erläuterten) Darstellung ist nun das der stetigen Aufeinanderfolge der Töne entsprechende Bild nicht sowohl die logarithmische Spirale auf der Zylinderfläche, als vielmehr die Schraubenfläche, welche ein Halbmesser des Zylinders beschreibt, wenn er in der Achse des Zylinders sich erhebt und sich zugleich um dieselbe dreht, und zwischen Erhebung und. Drehung der Relation u = 2^x – 1, oder was dasselbe, x = log₂ (1 + u) stattfindet. Hebt man, wie in der musikalischen Tonfolge c, d, e, f, g, a, h, c geschieht, nur eine bestimmte Anzahl von Tönen, mit Überspringung der zwischenliegenden, aus, so geben die ihnen entsprechenden Linien das Bild einer Wendeltreppe. Die Ausdrücke Tonleiter, Tonstufen sind also, wenn man zugleich an die Windung der Leiter denkt, in der Tat sehr treffend gewählt....."

    "So viel mir bekannt, hat zuerst W. Opelt (Über die Natur der Musik. Plauen und Leipzig 1834. S. 43) die obige zylindrische Spirale zur Versinnlichung der Tonreihe benutzt. Von der Schraubenfläche, die mir das Bild erst zu vervollständigen scheint, macht er keinen Gebrauch."

    Soweit die Darstellung von Drobisch, welche unstreitig sehr geeignet ist, von der Verbindung des progressiven und periodischen Elementes in der Tonreihe eine anschauliche Vorstellung zu geben.

    Zeigen wir nun zuvörderst, wie unter Wahl bloß anderer Einheiten diese Konstruktion mit unseren bisherigen Maßausdrücken in Beziehung tritt.

Sei n¢die Schwingungszahl eines beliebigen Grundtones, n die eines dagegen betrachteten anderen Tones,  = y ihr Verhältnis, x die Empfindung des Unterschiedes zwischen n und n', d. i. die Empfindung ihres Intervalls, k unsere gewöhnliche Konstante, so gibt die Unterschiedsformel

                                                                    x = k log .

(welcher Ausdruck noch mit log 2 zu dividieren sein würde, wenn man statt eines logarithmischen Systems mit der Grundzahl 2 das gewöhnliche anwenden wollte).

    Stellen wir nun die Werte von x, welche nach dieser Formel gegebenen Werten von n entsprechen, durch Bogen eines Kreises vom Radius 1 dar, welche von einem bestimmten Anfangspunkte an genommen sind, so ist 2p der Umfang dieses Kreises und zugleich Repräsentant des Oktavenintervalls. Jedesmal, wenn n eine Potenz der Grundzahl 2 wird, d. h., wenn der Ton auf eine höhere Oktave steigt; wird log eine ganze Zahl, mithin x ein Multiplum von 2p nach einer ganzen Zahl, d. i. gleich einer ganzen Zahl Kreisumfänge, oder kehrt x in der Konstruktion zum Ausgange zurück, welcher stattfindet, wenn n = 2, d. h. gleich der Schwingungszahl des Grundtones ist. Stellen wir nun zugleich das Schwingungsverhältnis

= y durch gerade Linien dar, die in den Endpunkten des Bogens x senkrecht auf der Ebene des Kreises stehen u. s. f., wie Drobisch, so haben wir ganz dessen Konstruktion.

    Auch lassen sich die, beiderseits untergelegten, mathematischen Ausdrücke leicht auf einander reduzieren. Nach Drobisch hat man y = 2^x, mithin

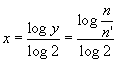
oder, wenn man, wie Drobisch selbst für die Anwendung der Logarithmen im Tongebiete vorgeschla-gen, 2 als die Grundzahl des logarithmischen Systems und zugleich mit uns als Grundzahl der Töne nimmt

x = log

wonach nur der Unterschied zwischen Drobisch’s und unserer Formel übrig bleibt, daß dieselbe Constante k, die wir = 2p setzen, von ihm = 1 gesetzt wird, was mitführt, daß bei ihm der Radius des Kreises = , der Umkreis = 1, bei uns der Radius = 1, der Umkreis = 2p gesetzt ist. Da nun beidesfalls das Oktavenintervall durch einen Kreisumfang repräsentiert wird, so hat dieses auch bei Drobisch den Wert 1, bei uns den Wert 2p , wovon Ersteres insofern angemessener erscheint, als die Oktave die natürliche Maßeinheit für die Tonintervalle bildet. Da es sich jedoch hier nicht um Darstellung der Tonverhältnisse in Zahlen, sondern durch Geometrie handelt, hat es gegenteils etwas für sich, den Radius wie gewöhnlich durch 1, den Umfang durch 2p auszudrücken; und schließlich bleibt die Wahl der Einheiten für die Konstruktion gleichgüllig.

    Übrigens sieht man nach einem Blicke auf unsere Formel leicht, daß der Gang der Ton-eindrücke noch einfacher, als durch eine, um einen Zylinder gewickelte, Spirale, durch eine ebene Spirale dargestellt werden kann, wenn man die Gleichung

                                                                                            x = 2p log 

durch Polkoordinaten darstellt, dabei x insbesondere als Winkel, und entweder log  oder  als Radiusvektor betrachtet, wovon Ersteres eine archimedische, Letzteres eine logarithmische Spirale gibt. Beidesfalls hat man in dem Winkel, welchen der Radiusvektor gegen seine beim Werte n = 2 stattfindende Ausgangslage bildet, das Maß der empfundenen Abweichung vom Grundtone oder von irgend einer Oktave des Grundtones; erstenfalls (im Falle der archimedischen Spirale) im Radiusvektor log  das Maß der empfundenen Höhe über dem Grundtone, sofern x = 2p log  proportional mit log  bleibt, zweitenfalls (im Falle der logarithmischen Spirale) im Radiusvektor  das Maß der wirklichen oder objektiven Höhe über dem Grundtone, wenn das relative Verhältnis der Schwingungszahlen des betreffenden Tones und Grundtones so genannt wird. Beidesfalls kann man dann noch, wie es Drobisch vorschreibt, den Radiusvektor während seiner Drehung sich erheben lassen, und durch die Erhebung  erstenfalls die wirkliche Höhe über dem Grundtone, zweitenfalls durch die Erhebung log  die empfundene Höhe über dem Grundtone dazu darstellen; so daß man beidesfalls, nur in verschiedener Form, mit der empfundenen Abweichung vom Grundtone oder einer Oktave desselben zugleich die empfundene Höhe über dem Grundtone samt der wirklichen Höhe darüber dargestellt findet, was ein kleiner Vorteil der Vollständigkeit sein dürfte. Durch beide Konstruktionen erhält man das Spiralblatt einer Schnecke, durch die erste ein verhältnismäßig mehr in die Höhe gezogenes, in der Schneckenachse endlich abschließendes, durch die zweite ein mehr in die Weite gedehntes, mit unendlich viel Windungen der Achse asymptotisch zustrebendes.

    Dies trifft interessanterweise damit zusammen, daß ein Spiralblatt in ein paar Windungen einen der wichtigsten Teile unseres Gehörorganes, den Träger eines Teiles der Endausbreitang des Gehörner-ven, darstellt. Ist man doch sogar geneigt gewesen, den Schneckennerven vorzugsweise vor dem Labyrinthnerven für die Empfindung der Tonhöhen bestimmt zu halten; doch ruht dies auf nichts Positivem; und sollte jenem Zusammentreffen eine mehr als zufällige Bedeutung beigelegt werden, so müßte die Ohrschnecke gerade so viel Windungen zeigen, als wir Oktaven vernehmen können, was nicht der Fall ist, wenn man nicht etwa annehmen will, daß der Labyrinthnerv die Skala der Schnek-kentöne fortsetzt. Jedesfalls würde es einiges Interesse haben, die genaue Form des Spiralblattes unserer Ohrschnecke aufzusuchen, und noch mehr, sich teleologische Rechenschaft von der Form desselben geben zu können; wozu aber bis jetzt keine Aussicht sein dürfte, und was uns auch hier nicht wesentlich angeht.

    Das Vorige ist nach Allem nur eine wenig wesentliche Transformation der ursprünglichen Darstellung von Drobisch, worauf kein Gewicht liegt, und die hier nur insofern angeführt wird, als sie sich so zu sagen von selbst als der natürlichste Ausdruck einer Begründung der dargestellten Verhältnisse dargeboten hat, auf die ich jetzt komme.

    Zunächst nämlich darf man nicht übersehen, daß alle diese Konstruktionen nur empirische sind, welche zwar die erfahrungsmäßigen Verhältnisse getreu darstellen, ohne uns aber etwas vom Grunde der dargestellten Verhältnisse zu lehren. Eine höhere oder tiefere Oktave tritt mit einer für das Gefühl maßgebenden Bedeutung ein, wenn sich eine Schwingungszahl verdoppelt oder halbiert, daher die Zahl 2 als eine fundamentale Konstante in die Formeln eingeführt ist, auf welcher diese Konstruktionen ruhen. Aber warum könnte nicht 3, 4, ³/₂ oder irgend eine Irrationalzahl diese Konstante sein, wonach dann statt der Oktave irgend ein anderes Intervall die maßgebende Bedeutung haben würde, welche in Wirklichkeit die Oktave hat. Der Toneindruck kehrt in gewissem Sinne zum Ausgangspunkte hei jeder Oktave zurück, daher die Kreisfunktion 2p als eine zweite fundamentale Konstante in unsere Formel eingeführt und diese durch Polkoordinaten von uns dargestellt ist; aber welcher in der Natur der Sache liegende Grund bringt dies mit sich? Von der auf das Weber’sche Gesetz gegründeten Formel

ausgehend; könnten wir für k eben so gut jeden anderen Wert als 2p substituieren, und statt Polkoordinaten eben so gut rechtwinklige Koordinaten zur Darstellung des Größenverhältnisses zwischen x und  oder log benutzen, wo wir dann eine gewöhnliche logarithmische Kurve, aber keine Spirale erhalten würden, womit der Ausdruck der Periodizität wegfallen würde. Warum ferner betrifft das periodische Element bloß die Höhe, nicht die Stärke, warum tritt es entschieden bloß im Gebiete der Töne, nicht der Farben auf? Auf alles dies gibt uns die Konstruktion keine Antwort, sondern verlangt vielmehr erst die Antwort.

    Es hat mich nun sehr überrascht, etwas, was mir eine Antwort darauf scheint, ungesucht mit zu erhalten, als ich etwas Anderes, allerdings damit Zusammenhängendes, suchte, nämlich nur darauf ausging, die gemeinsame Abhängigkeit des Toneindruckes von Schwingungszahl und Amplitude, welche nach den obigen Erörterungen durch die Erfahrung gefordert scheint, durch eine Ableitung aus elementaren Voraussetzungen wiederzufinden, ohne daran zu denken, daß die Abhängigkeit des periodischen Oktaveneindruckes solidarisch damit gegeben sein könnte, wie es sich wirklich gezeigt hat; ein Ergebnis, was ich aus dem 4fachen Gesichtspunkte für wichtig halte, als der Gesamtheit des Maßausdruckes für den Toneindruck dadurch der Stempel der Triftigkeit aufgedrückt wird, als das tief greifende Prinzip elementarer Ableitung, durch die dies Ergebnis gefunden wurde, sich damit bewährt, als ein psychophysisches Rätsel damit gelöst wird, und als eine, durch anderweite, künftig (Kapitel 33) darzulegende, Gründe schon wahrscheinlich, aber doch nur wahrscheinlich zu machende, Ansicht von der Einfachheit der Schwingungsbewegungen, welche unserem Hören innerlich unterliegen, und minderen Einfachheit derer, welche dem Sehen unterliegen, dadurch gestützt, hiermit der inneren Psychophysik nach einer gewissen Richtung vorgearbeitet wird. Nur unter der Voraussetzung nämlich, daß der Schallreiz die einfachst mögliche Schwingungsform in unserem empfindenden Gehörapparate auslöst, ergibt sich die folgende Erklärung.

    Ausführlicher wird dieser Gegenstand von mir im 32. Kapitel behandelt werden; ich hebe aber aus den etwas weitschichtigen Erörterungen, welche die allgemeinere Fassung der Aufgabe dort nötig machen wird, hier vorgreifend und resümierend Dasjenige heraus, was sich auf unsere jetzige Frage insbesondere bezieht.

    Im 32. Kapitel wird gezeigt werden, daß sich das Maß des Gesamteindruckes der Stärke und Höhe eines Tones von der Form log an oder log an², zwischen welchen nach den obigen Erörterungen noch die Wahl ist, durch Summation der Maße elementarer Empfindungsbeiträge wiederfinden läßt, welche durch die einzelnen Momente der Schwingung erzeugt werden, wenn man jeden elementaren Empfindungsbeitrag entweder von der in diesem Momente stattfindenden Geschwindigkeit (was die Form log an gibt) oder Geschwindigkeitsänderung (was log an² gibt) in derselben Weise abhängig denkt, als die ganze Empfindung von der ganzen Amplitude und Schwingungszahl abhängt.

    Bei dieser Herleitung sondert sich nicht nur von selbst Dasjenige, was in dem Maßausdrucke für den Ton von der Größe der Amplitude und was von der Größe der Schwingungsdauer abhängt, sondern man findet außerdem in den Maßausdruck einen Wert eingehend, welcher unabhängig von der Größe der Amplitude und Größe der Schwingungsdauer bloß von der periodischen Wiederkehr derselben Schwingungsdauer abhängt, und für einfache Schwingungen von jeder Amplitude und jeder Schwingungsdauer derselbe bleibt, in den Formen des Maßausdruckes log an oder log an² aber nur deshalb nicht zum Vorschein kommt, weil er, seiner konstanten Natur gemäß, in den gleich 1 gesetzten Konstanten k und a₁ n₁ oder a₁n₁² dieser Formen ¹⁷⁾ mit aufgeht, wie sich aus der folgenden Herleitung zeigt. Dieser Wert ist eine Funktion beider fundamentaler Konstanten 2 und p , wovon die Bedeutung des Oktavenintervalls abhängt, und zwar wird er ohne Rücksicht auf willkürliche Bestimmung der Maßeinheiten und der Konstante k, gleicherweise nach beiden Voraussetzungen, zwischen welchen noch die Wahl ist, absolut durch  gegeben, was dem obigen Werte von x für eine der Einheit gleich gesetzte Schwingungszahl n entspricht und als der reine Ausdruck des von der Periodizität der Bewegung abhängigen periodischen Elementes der Tonhöhenempfindung angesehen werden kann. Er geht nämlich ausschließlich aus der Summation einer periodischen Funktion hervor, in welche die Schwingungsdauer oder Schwingungszahl, nicht die Amplitude eingeht, kann daher nur mit erster (also mit der Tonhöhe), nicht letzter in Beziehung gesetzt werden, enthält aber, wie man sieht, nicht selbst die Schwingungsdauer; diese und die Amplitude gehen von anderer Seite in den Maßausdruck des gesamten Toneindruckes ein.

¹⁷⁾ Man erinnere sich, daß ihr entwickelter Wert eigentlich k log oder k log  ist.
 
 

In einer einfachen geradlinigen Schwingung von der Amplitude a, Schwingungsdauer t oder damit reziproker Schwingungszahl n =  ist die Geschwindigkeit v zur Zeit t, diese vom Maximum der Ausweichung an gerechnet, bekanntlich ¹⁸⁾

wo p die Ludolf’sche Zahl, oder die halbe Kreisperipherie, den Radius = 1 gesetzt. Indem nun der Empfindungsbeitrag in jedem Momente dt von der darin stattfindenden Geschwindigkeit v, oder was bei der logarithmischen Form des Ausdruckes wesentlich auf dasselbe herauskommt, lebendigen Kraft v² abhängig gemacht wird, wird er durch

                                                                                    k log dt oder k log dt

gegeben, wovon erster Ausdruck zu Grunde gelegt werden mag, mit Rücksicht, daß  stets als positiv zu nehmen ist. Hierin bedeutet b den Wert von v, bei dem der Empfindungsbeitrag auf die Schwelle tritt (die Elementarschwelle), und k die gewöhnliche Konstante. Hiernach wird die Empfindungssumme St, welche während der Dauer einer Schwingung erzeugt wird, gegeben durch

        ¹⁸⁾ Man sehe z. B. Herschel über das Licht §. 569 mit Rücksicht auf den Wert .

 
Da die Einheit der Geschwindigkeit willkürlich ist, setzen wir (um die Ausdrücke, auf die es hier ankommt, in einfachster Form zu gewinnen) den Wert = 1, zerlegen den Logarithmus des Produktes in eine Summe von Logarithmen, und substituieren n für , wodurch wir die Summe folgender drei Glieder erhalten:

wovon das erste den von der Amplitude, das zweite den von der Schwingungszahl oder Schwingungsdauer, das dritte den von der Periodizität der Schwingung abhängigen Teil des Maßausdruckes darstellt. Setzt man die Phase , so geht das letzte Glied über in

Das bestimmte Integral aber, welches den von der Periodizität rein abhängigen, von der Größe der Schwingungsdauer unabhängigen, Teil des Maßausdruckes, multipliziert mit dem konstanten Faktor , darstellt, ist

wonach der ganze Maßausdruck für die Empfindungssumme St während einer Schwingung von der Dauer t ist

    Dividiert man diesen Ausdruck mit t , wodurch man statt der Empfindungssumme die Intensität der Empfindung erhält, und setzt k = 2p , so erhält man als Maß der Intensität

oder, wenn man bei der Herleitung k = 1 und b = p setzt, den einfachsten Ausdruck

                                                                                                       log a n.

    Wie man zur Form k log  gelangt, wird im 32. Kapitel angegeben.

    Die zweite Voraussetzung, daß die Empfindung von der Geschwindigkeitsänderung (Geschwindigkeit zweiter Ordnung) abhängt, führt nach einem ganz entsprechenden Gange zu demselben Ausdrucke 2p log  für das periodische Element insbesondere, als die vorige Voraussetzung, und gibt als definitiven Werth für den ganzen Maßausdruck

welchen man durch Setzung von b = 8p²a und k = p in

2p log