Nach den Erörterungen des 22. Kapitels über die Unterscheidung von Empfindungsunterschieden und empfundenen Unterschieden oder Kontrastempfindungen kann unsere, zum Maße der ersten dienende, Unterschiedsformel nicht zugleich das Maß der letzten gewähren. In der Tat enthält sie bloß eine Abhängigkeit des Empfindungsunterschiedes von der Groöß der Reize, aber keine Abhängigkeit von den Umständen, von welchen die Größe des empfundenen Unterschiedes noch außerdem abhängt, und die Tatsache der Unterschiedsschwelle liegt nicht in ihr eingeschlossen, wonach sie auch keine Scheide zwischen bewußten und unbewußten empfundenen Unterschieden gewährt, die doch in der Wirklichkeit nicht minder als für absolute Empfindungen besteht. Zum Maße der empfundenen Unterschiede hat uns vielmehr eine andere Formel zu dienen, welche diesen Forderungen genügt, und welche ich die Unterschiedsmaßformel nenne, da sie für das Maß empfundener Unterschiede dasselbe leistet, als die Maßformel für das Maß absoluter Empfindungen.

        ¹⁾ In Sachen S. 9. 11. Revision S. 185 ff, Psych.Maßprinzipien S.194. 200.
 
 

    Mit Rücksicht darauf, daß empfundene Unterschiede so gut ihren Schwellenwert haben, als absolute Empfindungen, kann man zuvörderst die Unterschiedsmaßformel auf eine Analogie mit der Maßformel wie folgt begründen.

    Bezeichnen wir, wie früher einen Empfindungsunterschied, so jetzt einen empfundenen Unterschied zwischen den Empfindungen g und g' mit u, das zugehörige Reizverhältnis  mit j , und geben dem Werte dieses Reizverhältnisses, bei welchem der empfundene Unterschied auf die Schwelle tritt, d. i. der Verhältniskonstante oder Verhältnisschwelle v dasselbe Verhältnis zu jals die einfache Schwelle b zu dem Reize b in der Maßformel hat, so erhalten wir

    An sich hindert jedoch nichts, auch den kleineren Reiz im Zähler zu verwenden, nur hat man bei dieser umgekehrten Stellung beider Reize dann Alles in voriger Formel umzukehren, nämlich, indem man das Reizverhältnis j in das reziproke j₁ = verkehrt, auch den Wert von v in den reziproken v₁ =  zu verkehren, und die Stellung von j₁ und v₁, gegen die von j und v zu verkehren, also die Formel zu schreiben

welche mit der vorigen gleichen Wert hat, sofern .

    Im Folgenden wird aber die Voraussetzung j > 1 und demgemäß Stellung des größeren Reizes in den Zähler immer festgehalten werden, wonach man, wenn etwa ein in gewisser Weise angebrachter Reiz nach Umständen wechselnd größer und kleiner als der andere wird, auch seine Stelle als Zähler und Nenner im Werte von j zu wechseln hat.

    Die obige Aufstellung der Formel setzt ferner allgemein gesprochen den Normalfall voraus, daß, wenn die zwei zeitlich oder räumlich verschiedenen Reize, deren Unterschied es aufzufassen gilt, die Größe mit einander vertauschen, so daß der größere Reiz an die Stelle des kleineren tritt und umgekehrt, nur die Richtung, nicht die Größe des empfundenen Unterschiedes sich ändert. Dieser Normalfall ist keineswegs der allgemeine Fall der Wirklichkeit, da vielmehr in allen Fällen, wo sich bei Versuchen über die Unterschiedsempfindlichkeit sog. konstante Fehler in der Auffassung eines Unterschiedes je nach Raum- und Zeitlage der verglichenen Größen zeigen (vgl. Th. I. S. 90), die Empfindung des Unterschiedes bei gleichem Größenverhältnisse der Reize verschieden groß ausfällt, je nachdem man den einen oder anderen Reiz zum größeren macht. Die Bewährung des Weber’schen Gesetzes, auf welchem unsere Formel fußt, setzt aber die Abwesenheit oder Elimination konstanter Fehler voraus.

    Nun aber lassen sich konstante Fehler wirklich immer durch Versuch und Rechnung eliminieren, und so die Fälle mit konstanten Fehlern auf den Normalfall zurückführen, in vielen Fällen sind auch konstante Fehler zu gering, um eine Berücksichtigung nötig zu machen, endlich können solche, nachdem die Grundformel für den Normalfall gegeben ist, dann in geeigneter Weise noch besonders berücksichtigt werden (vgl. Kap. 27); wonach die Aufstellung der Formel für den Normalfall immer das bleibt, wovon man auszugehen hat.

    Zu derselben Form der Unterschiedsmaßformel, die hier bloß nach Analogie aufgestellt und mithin noch nicht streng begründet erscheint, einschließlich der Regel bezüglich der Änderung der Form der Formel, je nachdem man j > 1 oder < 1 macht, läßt sich strenger auf Grund des Weber’schen Gesetzes und der Tatsache der Verhältnissschwelle nach einem analogen Gange als zur Maßformel auf die in folgender Einschaltung angegebene Weise gelangen.

    Die auf das Weber’sche Gesetz gestützte Fundamentalformel gibt für zwei Empfindungsunterschiede insbesondere

hiernach

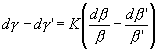
    Indem nun g und g' zwei Empfindungen sind, deren Unterschied g - g' ist, kann das Differenzial hiervon dg - dg ' als das Element eines Empfindungsunterschiedes angesehen werden, dessen Wert  ist. Sofern aber die Hinzufügung einer Konstante zu einem Integrale nichts im Differenziale ändert, ist dg - dg ' zugleich allgemeiner das Element eines um eine Konstante (d. i. von j oder  unabhängigen Größe) vermehrten oder verminderten Empfindungsunterschiedes. Nun läßt sich nach Kap. 22 der Empfindungsunterschied mit dem besonderen Falle eines empfundenen Unterschiedes identifizieren, wo bei kleinstmöglicher Differenz der Reize b , b ' ein Unterschied empfunden wird, und ein empfundener Unterschied als der allgemeinere Fall ansehen, wo bei irgend einem bestimmten Werte von  die Empfindung des Unterschiedes beginnt und schwindet. Durch Integration des obigen Wertes von dg - dg ' und Konstantenbestimmung in gleich anzuzeigender Weise erhalten wir den Ausdruck für diesen allgemeineren Fall und hiermit die Unterschiedsmaßformel.

    In der Tat, setzen wir dg - dg ' ± du (sofern an sich kein Grund ist, das eine Vorzeichen vor dem anderen anzuwenden), so haben wir

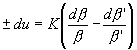
Dies gibt durch Integration unter Anwendung natürlicher Logarithmen

= K log j + C

    Und dieser Wert, in die allgemeine Gleichung substituiert, gibt

Unter Anwendung des oberen Vorzeichens haben wir also

unter Anwendung des unteren und Umkehr des Vorzeichens auf beiden Seiten

    Die Formel (1) entspricht der Bedingung, daß logj positiv ist und mithin der größere Reiz in den Zähler gesetzt wird, die Form (2) eben so der Bedingung, daß logj negativ ist, mithin der kleinere Reiz in den Zähler gesetzt wird, weil nur unter dieser Voraussetzung u mit Wachstum des absoluten Wertes von j in positivem Sinne wachsen kann, so lange der von uns vorausgesetzte Normalfall besteht. Unterscheiden wir die beiden Fälle, daß der größere und daß der kleinere Reiz in den Zähler gesetzt wird, dadurch, daß wir erstenfalls die Buchstaben j und v, zweitenfalls j₁ und v₁ verwenden, so wird, insofern beide Fälle sich auf dieselbe Empfindung u beziehen, und also ihr Maß bloß formell verschieden sein kann

mithin

sein müssen, was voraussetzt, da j₁ = , daß auch v₁ =  sei.

    Wenn der Normalfall nicht stattfände, sondern u verschiedene Werte annähme, je nachdem die Lage des größeren und kleineren Reizes vertauscht wird, so würden sich die Gleichungen (1) und (2) immer noch zur Aufstellung der Unterschiedsmaßformel verwenden lassen, insofern der konstante Fehler das Weber’sche Gesetz, wonach bei gleichem j der empfundene Unterschied gleich groß bleiben muß, für die eine, wie für die entgegengesetzte Lage des größeren und kleineren Reizes insbesondere bestehen ließe. Dann hätte man nämlich nur nötig, die Konstante v für die entgegengesetzte Zeit- und Raumlage der verglichenen Größen verschieden zu bestimmen. Sofern aber hierbei der Fall eintreten sollte, daß vermöge des konstanten Fehlers innerhalb gewisser Grenzen der kleinere Reiz als der größere erschiene und der empfundene Unterschied wüchse, wenn sich der Unterschied der Reize verkleinerte statt vergrößerte, würde man für diesen Fall unter Festhaltung der Regel, den größeren Reiz stets im Zähler zu verwenden, in jenen Grenzen die Gleichung (2) statt (1) anzuwenden haben, oder die Regel, den größeren Reiz im Zähler zu verwenden, exzeptionell in die gegenteilige zu verkehren haben, um noch die Gleichung (1) anzuwenden, damit stets positive Werte den bewußten Werten des empfundenen Unterschiedes entsprechen.

    Wie bei den früheren Formeln bedarf auch bei der Unterschiedsmaßformel die Bedeutung des Vorzeichengegensatzes, welchen der Empfindungswert annehmen kann, einer besonderen Klärung.

    Zur vollen Bestimmtheit des Wertes u ist nicht bloß auf das Vorzeichen von u selbst, sondern auch auf das Vorzeichen der Empfindungen, zwischen denen der Unterschied besteht, zu achten. Der empfundene Unterschied u nimmt nach der Herleitung bloß dann beim Werte j = v den Wert Null als Grenze zwischen bewußten und unbewußten Werten an, wenn das Verhältnis jzwischen Reizen oberhalb der Schwelle besteht, denn nur hierauf bezieht sich die erfahrungsmäßige Bestimmung der Konstante v, wogegen, wenn beide Reize und hiermit die zugehörigen Empfindungen unter die Schwelle fallen, hiermit der ganze Begriff eines empfundenen Unterschiedes verloren geht, und wenn bloß ein Reiz oberhalb der Schwelle, der andere auf der Schwelle oder unter der Schwelle ist, es so gut ist, als wenn man bloß mit einer einzigen Empfindung, als Differenz von einer Nullempfindung oder von einer gar nicht wirklichen Empfindung, zu tun hätte.

    Dies ist deshalb zu erinnern nötig, weil, nach der Formel u = k (log j - log v), der Wert von u positiv ausfallen kann, auch wenn beide Reize b, b ' unter der Schwelle sind, mithin gar nichts empfunden wird, indem hierzu hinreicht, daß j > v, was sehr wohl der Fall sein kann, wenn sowohl b als b' unter der Schwelle ist, wofern nur b ein großes Verhältnis zu b' hat. Man darf dann in diesem positiven Werte von u noch nicht das Zeichen des Bewußtseins finden, weil die Vorbedingung dazu fehlt, das Bewußtsein der Werte, von denen u abhängt.

    Sollte gegen diese verschiedene Deutung des Vorzeichens von u, je nachdem u Funktion so oder so beschaffener Werte b, b ' ist, noch ein Bedenken bestehen, so wird es sich wieder, wie schon früher so manches entsprechende Bedenken, durch Verweisung auf einen analogen Fall der analytischen Geometrie heben lassen. Auch in dieser kann das Vorzeichen eines Wertes u, welcher Funktion zweier Werte b, b ' ist, eine sehr verschiedene Bedeutung annehmen, je nachdem die Werte b,b ' so oder so beschaffen sind.

    In der Tat, nehmen wir ein Quadrat mittelst eines, durch seinen Mittelpunkt gelegten, den Seiten parallelen Kreuzes in vier kleinere Quadrate geteilt, die durch r. o, l. o, r. u, l. u (rechts oben, links oben, rechts unten, links unten) bezeichnet sein mögen, und suchen wir den analytischen Ausdruck u für die 4 kleinen Quadrate. Der von der Mitte ausgehende rechte Arm des Kreuzes werde seiner Maßzahl nach durch + b bezeichnet, so wird der linke durch - b bezeichnet werden; der von der Mitte nach oben gehende Arm des Kreuzes werde durch + b' bezeichnet, so wird der nach unten gehende Arm durch - b' bezeichnet werden; und wir werden durch Multiplikation dieser respektiv positiven und negativen Maßzahlen mit einander erhalten als analytischen Ausdruck u für

    Anstatt die Unterschiedsmaßformel als Funktion des Reizverhältnisses und der Verhältnisschwelle aufzustellen, können wir sie auch als Funktion des relativen Reizunterschiedes und der Unterschiedskonstante wie folgt aufstellen.

    Sei der eine Reiz vom anderen um die Größe a , und die Verhältnisschwelle v von 1 um die Größe w verschieden, so hat man

Hierin ist  der relative Reizunterschied, der kurz J heiße, und w die Unterschiedskonstante in dem Th. I. S. 244 angegebenen Sinne. Wonach die Unterschiedsmaßformel folgende Form annimmt

    In dem Falle, wo J und w kleine Werte sind, deren Quadrate sich gegen die erste Potenz vernachlässigen lassen, geht nach der i. Kap. 14 angezeigten Substitution diese Formel über in

    In dem Normalfalle, auf den sich die Aufstellung unserer Formel bezieht, ist v stets größer als 1, so lange nicht die Grenze der Unterschiedsempfindlichkeit erreicht ist. Wo aber die Reize unter günstigen Verhältnissen, ihren Unterschied aufzufassen, sich befinden, und die Unterschiedsempfindlichkeit groß ist, weicht v immer nur wenig von 1 ab, wie sich z. B. bei den Versuchen über die Unterschiedsempfindlichkeit für das Licht gezeigt hat, wo nach Volkmann  gefunden wurde. Indem dann log v wenig von Null abweicht, fällt auch die Unterschiedsmaßformel nahe mit der einfachen Unterschiedsformel zusammen, und diese kann statt jener approximativ so lange dienen, als nicht auch j auf einen der Einheit sehr nahen Wert und mithin log j auf einen der Null nahen Wert herabkommt.

    Die Verhältnisschwelle v tritt, wie man sieht, in der Unterschiedsmaßformel ganz an die Stelle der Reizschwelle b in der Maßformel, und ist eben so maßgebend für den Grad der Empfindlichkeit, mit welchem ein gegebenes Reizverhältnis aufgefaßt wird, als die Konstante b für den Grad der Empfindlichkeit, mit welchem ein gegebener Reiz aufgefaßt wird. So wie  als Maß der absoluten Empfindlichkeit, kann  als Maß der relativen Unterschiedsempfindlichkeit dienen. Alles hat auf den Wert von v Einfluß, wodurch bei gegebenem Reizverhältnisse der empfundene Unterschied abgeändert wird, und es ist also v als eine Konstante nur für konstante Verhältnisse der Auffassung anzusehen.

    Zu den einflußreichen Umständen auf den Wert von v gehört außer der zeitlichen und räumlichen Differenz der Reize, deren Unterschied es aufzufassen gilt, die Beschaffenheit dessen, was sich dazwischen einschiebt, so wie, was zeitlich und räumlich umliegt. Dieser Einfluß kann so beschaffen sein, daß konstante Fehler in der Auffassung des Unterschiedes entstehen, die durch Versuche und Rechnung in der bei den Maßmethoden der Unterschieds- empfindlichkeit und im 27. Kapitel angegebenen Weise zu berücksichtigen sind.

    Der Grad der absoluten Empfindlichkeit, mit welchem beide Reize aufgefaßt werden, hat, sofern er sich für beide Reize immer gleich bleibt, keinen Einfluß auf den Wert des empfundenen Unterschiedes; indes ein ungleicher Wert derselben für beide Reize einen konstanten Fehler begründet, welcher die dafür zu nehmenden Rücksichten nötig macht.

    Wie jede Veränderung der Konstante b in der Maßformel auch durch eine reziproke Veränderung der Reizwirkung b vertreten werden kann, gilt das Entsprechende von der Veränderung der Konstante v, sofern jede Veränderung derselben durch eine reziproke Veränderung von j vertreten werden kann.

    Der Ausdruck für eine vollbewußte Empfindung in dem Kap. 22 angegebenen Sinne wird, sofern sie sich als besonders aufgefaßter Unterschied einer Empfindung oberhalb der Schwelle von einer Empfindung auf der Schwelle, d. i. von einer Nullempfindung fassen läßt, natürlicherweise gefunden, wenn wir in der Unterschiedsmaßformel den kleineren Reiz b', zu dem wir den anderen im Verhältnisse betrachten, auf den Schwellenwert b reduzieren, indes wir zugleich die Empfindung g¢ auf Null reduzieren, mithin für j =  substituieren , und für u substituieren g . So erhalten wir diese Formel

    Nennen wir bv die Vollschwelle, b wie bisher schlechthin die Schwelle der Empfindung, so wird also das Verhältnis zwischen der Vollschwelle und Schwelle durch die Verhältniskonstante v gegeben sein. Schließen wir solche Ungleichförmigkeiten der absoluten Empfindlichkeiten und der Zeit- und Raumlage der Reize aus, welche machen können, daß ein größerer Reiz als der kleinere erscheint, so wird v stets größer als 1 sein, wenn  > 1, und also der Reiz vom Werte b an noch im Verhältnisse v wachsen müssen, um den Beginn des halbbewußten Zustandes der Empfindung in den vollbewußten überzuführen.

    Insofern es überhaupt gilt, die Grundformeln des psychischen Maßes zuerst für die einfachsten Voraussetzungen aufzustellen, und Alles, was als Abweichung kleiner Ordnung oder Komplikation die Aufstellung der Grundformen schon voraussetzt, anfangs zu vernachlässigen und erst nachtäglich zu berücksichtigen, ist auch bei der Aufstellung der Unterschiedsmaßformel und der sich daran knüpfenden Erörterung bisher ein Umstand nicht berücksichtigt worden, der als eine solche Abweichung oder Komplikation anzusehen ist, und darin besteht, daß das Dasein eines Reizes auf die Empfindlichkeit, mit welcher ein nachbarlicher Reiz aufgefaßt wird, einen Einfluß hat, welcher bei ungleichen Reizen, wie sie in die Unterschiedsmaßformel eingehen, ungleich für beide Reize ist. So, wenn Weiß und Schwarz neben einander sind, erscheint das Weiß heller, das Schwarz schwärzer, als in continuo ohne den ungleichen Nachbarreiz, was man die Hebung der Eindrücke durch den Kontrast nennt. Nun ist diese Hebung der Eindrücke von gewisser Seite unstreitig nur Sache eines Vergleichsurteils, daß wir nämlich das Schwarz gegen das Weiß, das Weiß gegen das Schwarz als Maßstab halten, oder das eine als ein Plus, das andere als ein Minus gegen das Andere fassen; und macht insofern keine besondere Rücksicht bei Aufstellung unserer Formeln nötig, da dieses Urteil über das Verhältnis der absoluten Empfindungen auf der Größe und Richtung des empfundenen Unterschiedes erst beruht, dieser aber nicht von ihm abhängt. Ja man könnte geneigt sein, die ganze Hebung der Eindrücke durch den Kontrast hiervon abhängig zu machen. Ich werde inzwischen später erfahrungsmäßige Tatsachen beibringen, welche dies nicht gestatten, vielmehr nötigen anzunehmen, daß, abgesehen von jenem Vergleichsurteile, die Empfindlichkeit für das Licht auf dem Weiß durch Nachbarschaft des Schwarz erhöht, auf dem Schwarz durch Nachbarschaft des Weiß vermindert gegen den Fall ist, daß wir bloß Weiß oder Schwarz im Gesichtsfelde haben, hiermit das Weiß wirklich absolut heller, das Schwarz dunkler erscheint, als in continuo allein ins Auge gefaßt, so daß beide mit diesen abgeänderten Werten zur Bestimmung des Vergleichsurteils selbst erst wirken. Dieser Umstand nun wird unstreitig ebenfalls einflußlos auf die Aufstellung und Verwendung der Unterschiedsmaßformel werden, wenn wir dieselbe statt auf den Reiz auf die dadurch ausgelöste psychophysische Bewegung (nach dem dafür statt b in die Formeln zu substituierenden Maße) beziehen, weil die abgeänderte Empfindlichkeit für einen Reiz selbst durch eine andere Größe von demselben auslösbarer psychophysischer Bewegung repräsentiert werden kann, und voraussetzlich die Grundformeln des psychischen Maßes eine reine und strenge Gültigkeit bezüglich der von den Verhältnissen der psychophysischen Bewegung abhängigen Empfindungsverhältnisse haben. Und selbst ohne den Rückgang auf die psychophysische Bewegung, die erst der inneren Psychophysik aufgehoben bleiben muß, würde es, wenn wir nur die Gesetze kennten, nach denen sich die Empfindlichkeit für die Reize durch Nachbarschaft derselben ändert, hinreichen, demgemäß abgeänderte Werte von b, b ' und mithin j , oder, was auf dasselbe herauskommt, v in die Unterschiedsmaßformel zu substituieren, um sie dann wie früher zu verwenden; auch liegt hiernach ein wichtiges Bedürfnis vor, diese Gesetze zu studieren. Auf dieses Studium werde ich später eingehen. So lange sie aber nicht bekannt sind, müssen wir uns begnügen, die Unterschiedsmaßformel als eine doch approximativ triftige in Fällen zu verwenden, wo kein Grund vorliegt, dem angegebenen Umstande einen erheblichen Einfluß zuzuschreiben, wie z. B. bei Schätzung der empfundenen Unterschiede zwischen Sternhelligkeiten, und übrigens der Richtung des Einflusses nur im Allgemeinen Rechnung tragen, denn unstreitig kommen viele Fälle vor, wo der betreffende Einfluß größer ist, als daß er mit Fug vernachlässigt werden könnte.