Die Empfindung steigt mit dem Reize auf, aber keineswegs demselben proportional auf. Vielmehr wissen wir, daß, während der Reiz bis zum Schwellenwerte ansteigt, die Empfindung überhaupt noch nicht bemerklich wird, und auch höher hinauf nicht in einem einfachen, sondern logarithmischen Verhältnisse dazu wächst. Es hat sein Interesse, die Hauptverhältnisse dieses Ganges noch etwas genauer zu verfolgen, als es durch die bloße Unterscheidung und Inbetrachtnahme der drei Hauptfälle, welche unter der Formel begriffen sind, bisher geschehen ist. Hierzu ist dieses Kapitel bestimmt.
Zu einfacherer Ableitung des bezugsweisen Ganges von Reiz und Empfindung soll die Maßformel folgends auf ihre einfachste Form g = log b reduziert gedacht werden, wobei der Schwellenwert b als Einheit des Reizes gilt, und die Reizwerte b die Bedeutung von Fundamentalwerten in dem (s. o.) angegebenen Sinne annehmen. Mit e soll wie immer die Grundzahl der natürlichen Logarithmen 2,718.... bezeichnet werden.
Allgemein entspricht jedem positiven
Empfindungswerte bei einem gegebenen Reize b
ein gleich großer negativer beim reziproken Reizwerte ![]() ; nach der allgemeinen Beziehung (Kap. 14 Formel 2), daß log
; nach der allgemeinen Beziehung (Kap. 14 Formel 2), daß log![]() =
- log b , wonach den beiden Reihen der Reizwerte
=
- log b , wonach den beiden Reihen der Reizwerte
1; ![]() ;
;![]() ;
; ![]() .....
.....
Sowohl die Reihe der positiven als
negativen Empfindungswerte läuft nach Maßgabe als man b
im Werte g = log b
oder g = log ![]() ins Unendliche wachsen läßt, in eine unendliche respektiv positive
oder negative Größe aus; wovon erstere eine unendlich starke
Empfindung, letztere das absolute Unbewußtsein einer Empfindung bezeichnet.
Was aber das Erste anlangt, so darf man nicht vergessen, daß unsere
Formel bloß so lange gilt, als das Weber’sche Gesetz gilt, und daß
dieses nach der Einrichtung unseres Organismus bei zu starken Reizeinwirkungen
gültig zu sein aufhört, daher sich die Empfindung durch Steigerung
des Reizes im Menschen nicht so ins Unbestimmte steigern läßt,
wie es nach abstrakter Geltung der Formel der Fall sein würde. Hingegen
hindert nichts, vorauszusetzen, daß, wenn die psychophysische Bewegung
ins Unbestimmte gesteigert werden könnte, auch die Abhängigkeit
der Empfindung davon ins Unbestimmte der Formel folgen würde.
ins Unendliche wachsen läßt, in eine unendliche respektiv positive
oder negative Größe aus; wovon erstere eine unendlich starke
Empfindung, letztere das absolute Unbewußtsein einer Empfindung bezeichnet.
Was aber das Erste anlangt, so darf man nicht vergessen, daß unsere
Formel bloß so lange gilt, als das Weber’sche Gesetz gilt, und daß
dieses nach der Einrichtung unseres Organismus bei zu starken Reizeinwirkungen
gültig zu sein aufhört, daher sich die Empfindung durch Steigerung
des Reizes im Menschen nicht so ins Unbestimmte steigern läßt,
wie es nach abstrakter Geltung der Formel der Fall sein würde. Hingegen
hindert nichts, vorauszusetzen, daß, wenn die psychophysische Bewegung
ins Unbestimmte gesteigert werden könnte, auch die Abhängigkeit
der Empfindung davon ins Unbestimmte der Formel folgen würde.
Die ganze Reihe der negativen Empfindungswerte von der negativen Unendlichkeit bis zur Schwelle entspricht dem verhältnismäßig kleinen endlichen Intervalle der Reizwerte von 0 bis 1, indes die Reihe der positiven Empfindungswerte von der Schwelle bis zur unendlich starken positiven Empfindung dem unendlichen Intervalle der Reizwerte von 1 bis ¥ zugehört.
Verfolgen wir des Weiteren nun den Gang der positiven Empfindungswerte.
Berechnet man unter Zugrundelegung
eines beliebigen logarithmischen Systems nach der Formel g=
log b die Werte g,
welche den von der Schwelle 1 an wachsenden Werten b
zugehören, so findet man, daß g anfangs
in rascherem Verhältnisse als b wächst,
wie sich darin zeigt, daß das Verhältnis ![]() anfangs
wächst. Steigert man aber b immer mehr,
so nimmt das zugehörige Verhältnis
anfangs
wächst. Steigert man aber b immer mehr,
so nimmt das zugehörige Verhältnis ![]() wieder ab. Kurz: steigert man den Reiz von seinem Schwellenwerte an, so
steigt die Empfindung anfangs rascher als der Reiz, über eine gewisse
Grenze hinaus aber langsamer.
wieder ab. Kurz: steigert man den Reiz von seinem Schwellenwerte an, so
steigt die Empfindung anfangs rascher als der Reiz, über eine gewisse
Grenze hinaus aber langsamer.
Da die Empfindung beim Schwellenwerte selbst Null ist, jeder endliche Wert aber unendlichemal so groß als Null, so geschieht die Steigerung der Empfindung bei Überschreitung des Schwellenwertes um eine noch so kleine endliche Größe in unendlich starkem Verhältnisse. Setzen wir anderseits den idealen Fall einer unendlichen Stärke des Reizes unter Forterhaltung der Gültigkeit der Formel, so wird ein endlicher Zuwachs des Reizes in keinem merklichen Zuwachse der Empfindung mehr gespürt. Der Übergang von einer Grenze zur anderen, wo die Empfindung in unendlichem Verhältnisse und wo sie gar nicht mehr merklich durch einen gegebenen endlichen Zuwachs des Reizes wächst, wird nun eben dadurch vermittelt, daß sie bis zu gewissen Grenzen rascher, über gewisse Grenzen hinaus langsamer als der Reiz wächst.
Hierzwischen muß es notwendig
einen ganz bestimmten Mittelfall geben, wo die Empfindung weder rascher
noch langsamer als der Reiz, sondern (streng genommen nur innerhalb eines
unendlich kleinen Intervalls) demselben proportional wächst. Und nachdem
bis zu diesem Mittelfalle der Wert ![]() =
= ![]() mit
Wachstum von b zunimmt, darüber hinaus
abnimmt, muß dieser Fall dem Maximum von
mit
Wachstum von b zunimmt, darüber hinaus
abnimmt, muß dieser Fall dem Maximum von ![]() entsprechen.
entsprechen.
Diese Bedingung gibt zugleich den Weg
an die Hand, den Reizwert b zu bestimmen, bei
dem dieser Wendepunkt eintritt. Nach bekannten Regeln der Differenzialrechnung
(durch Nullsetzung des Differenziales von ![]() )
findet man, daß der Wert b , welchem das
Maximum
)
findet man, daß der Wert b , welchem das
Maximum ![]() entspricht, gleich e, d. i. gleich der Grundzahl der natürlichen
Logarithmen ist. Wenn also der Reiz das 2,718... fache seines Schwellenwertes
ist, und sich von da um ein weniges ändert, so ändert sich die
Empfindung der Änderung des Reizes genau proportional.
entspricht, gleich e, d. i. gleich der Grundzahl der natürlichen
Logarithmen ist. Wenn also der Reiz das 2,718... fache seines Schwellenwertes
ist, und sich von da um ein weniges ändert, so ändert sich die
Empfindung der Änderung des Reizes genau proportional.
Steigt der Reiz weiter über diesen Wert, so wächst zwar die Empfindung noch absolut genommen, aber nimmt ab im Verhältnisse zum Reize. Sinkt er merklich darunter, so sinkt die Empfindung zugleich absolut und relativ zum Reize.
Der Punkt, wo dieses relative Maximum der Empfindung eintritt, soll der Kardinalpunkt heißen, und der Reizwert, bei dem es eintritt, also das e-fache des Schwellenwertes, und die zugehörige Empfindung der Kardinalwert des Reizes und der Empfindung.
Wenn also ein Reiz in der e-fachen Stärke seines Schwellenwertes oder mit seinem Kardinalwerte wirkt, so gibt er das verhältnismäßige Maximum der Empfindungsleistung oder die Kardinalempfindung. Und wenn man es daher in seiner Gewalt hat, ein gegebenes Reizquantum mehr konzentriert oder mehr verteilt zu verwenden, so wird man, um die größtmögliche Empfindungsleistung dadurch zu erhalten, dasselbe so zu verteilen haben, daß es mit der e-fachen Stärke des Schwellenwertes oder als Kardinalreiz wirkt. Konzentriert man es mehr, so wird die Empfindung intensiver; aber es wird eine so viel geringere Menge solcher intensiven Empfindungen entstehen, daß doch im Ganzen an Empfindungsleistung verloren wird; verteilt man es mehr, so wird die größere Menge der Empfindungen den Verlust durch die geringere Intensität nicht zu kompensieren vermögen. Später, bei den Verteilungsformeln der Empfindung, werden wir auf einem anderen Wege uns zu demselben Resultate geführt finden.
Da um jeden Maximumwert die Werte sich nur langsam ändern,
so wird auch ![]() um seinen Maximumwert beinahe konstant bleiben, und also nicht nur bei
dem Kardinalwerte des Reizes, sondern auch in der Nähe desselben die
Empfindung merklich proportional mit dem Reize wachsen.
um seinen Maximumwert beinahe konstant bleiben, und also nicht nur bei
dem Kardinalwerte des Reizes, sondern auch in der Nähe desselben die
Empfindung merklich proportional mit dem Reize wachsen.
Das funktionelle Verhältnis zwischen Reiz und Empfindung schließt also einige Spezialfälle von einer gewissen bevorzugten Bedeutung im bezugsweisen Gange beider ein, den Schwellenpunkt und Kardinalpunkt. Beim Schwellenpunkte ist die Empfindung Null, beim Kardinalpunkte hat sie das relative Maximum zum Reize. Der erste bezeichnet zum Aufsteigen des Reizes den Punkt, wo die negativen Werte der Empfindung in positive übergehen, der zweite den Punkt, wo die relative Zunahme zum Reize in relative Abnahme übergeht. Beim ersten steigt die Empfindung unendlich schnell verglichen mit dem Steigen des Reizes, beim zweiten steigt sie proportional mit dem Steigen des Reizes.
Hierzu kommt nun noch der formell wichtige Umstand, daß nach den Bestimmungen (s. Kap. 16) der Schwellenwert als Einheit des Reizes und der Kardinalwert als Einheit der Empfindung die einfachstmögliche Form der Maßformel (g = log b ), welche die Beziehung zwischen Reiz und Empfindung ausdrückt, für den Fall natürlicher Logarithmen geben, deren System eine mathematisch bevorzugte Bedeutung vor jedem anderen Systeme hat.
Hier folgt eine kleine Tabelle, welche für die Voraussetzung der Reizeinheit beim Schwellenwerte, und Empfindungseinheit beim Kardinalwerte die zu einander gehörigen Werte des Reizes und der Empfindung bei wachsendem Reize und wachsender Empfindung gibt, auf Seite I so, daß zu den gegebenen Reizgrößen die zugehörigen Empfindungsgrößen, auf Seite II umgekehrt angegeben sind.
Seite I ist mittelst natürlicher Logarithmen nach der Formel g= log b oder, was äquivalente Werte gibt, mittelst gemeiner nach der Formel
![]()
berechnet; Seite II nach der Formel
![]() .
.
In Betreff der beigefügten Werte ![]() ist zu bemerken, daß ihre absolute Größe keine Bedeutung
hat, da sie an den willkürlichen Einheiten von Reiz und Empfindung
hängt, sondern nur der davon unabhängige Gang oder die gegenseitigen
Verhältnisse dieser Werte mit Aufsteigen von g
und b.
ist zu bemerken, daß ihre absolute Größe keine Bedeutung
hat, da sie an den willkürlichen Einheiten von Reiz und Empfindung
hängt, sondern nur der davon unabhängige Gang oder die gegenseitigen
Verhältnisse dieser Werte mit Aufsteigen von g
und b.
|
|
|
|
|
|
|
| 0 | - ¥ | - ¥ | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 2,7183 | 0,36788 |
| 1,5 | 0,4055 | 0,27031 | 1,5 | 4,4817 | 0,33469 |
| 2 | 0.6931 | 0,34657 | 2 | 7,3891 | 0,27067 |
| 2,718 | 1,0000 | 0,36788 | 2,718 | 15,154 | 0,17938 |
| 3 | 1,0986 | 0,36620 | 3 | 20,086 | 0,14936 |
| 4 | 1,3863 | 0,34657 | 4 | 54,598 | 0,07326 |
| 5 | 1,6094 | 0,32188 | 5 | 148,41 | 0,03369 |
| 6 | 1.7918 | 0,29821 | 6 | 403,43 | 0,01487 |
| 7 | 1,9459 | 0,27799 | 7 | 1096,6 | 0,00640 |
| 8 | 2,0794 | 0,25993 | 8 | 2981,0 | 0,00268 |
| 9 | 3,1972 | 0,24413 | 9 | 8103,1 | 0,00088 |
| 10 | 2,3026 | 0,23026 | 10 | 22026 | 0,000051) |
1) Genauer 0,0000454.
Man sieht nun auf der Seite I, daß
dem Reize Null ein negativ unendlicher Wert der Empfindung entspricht,
d. h. der tiefst mögliche Grad des Unbewußtseins, das absolute
Unbewußtsein. Während der Reiz von Null bis l steigt, wo die
bewußte Empfindung beginnt, durchläuft die Empfindung alle mögliche
negative Werte, indem nach der Formel die in der Tabelle nicht mit angeführten
negativen Empfindungen für den Reiz ![]() u. s. f. den positiven für den Reiz 2, 3, 4 u. s. f. im absoluten
Zahlwerthe entsprechen. Wenn der Reiz über seinen Schwellenwerth 1
steigt, so wächst gemäß dem Angeführten die Empfindung
anfangs in rascherem Verhältnisse als der Reiz; indem das Verhältniss
u. s. f. den positiven für den Reiz 2, 3, 4 u. s. f. im absoluten
Zahlwerthe entsprechen. Wenn der Reiz über seinen Schwellenwerth 1
steigt, so wächst gemäß dem Angeführten die Empfindung
anfangs in rascherem Verhältnisse als der Reiz; indem das Verhältniss ![]() mit dem Wachstume von b anfangs wächst.
Bei b = e = 2,718, d. i. dem Kardinalwerte
des Reizes, zeigt sich das Maximum von
mit dem Wachstume von b anfangs wächst.
Bei b = e = 2,718, d. i. dem Kardinalwerte
des Reizes, zeigt sich das Maximum von ![]() =
= ![]() =
0,36788, und um diesen Wert von b = 2 bis b=
4 steigt die Empfindung merklich im Verhältnisse des Reizes, indem
das Verhältnis
=
0,36788, und um diesen Wert von b = 2 bis b=
4 steigt die Empfindung merklich im Verhältnisse des Reizes, indem
das Verhältnis ![]() hier nahe konstant bleibt; indes es bei weiterem Wachstume des Reizes immer
augenfälliger abnimmt.
hier nahe konstant bleibt; indes es bei weiterem Wachstume des Reizes immer
augenfälliger abnimmt.
Hier folgen noch nach voriger Tabelle
für die aufeinanderfolgenden Differenzen der Empfindung g,
wenn sie von 0 immer um die gleiche Größe 1 wächst, die
zugehörigen Differenzen des Reizes b.
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 |
1 1 1 1 1 1 1 1 1 |
4,6708 12,697 34,512 93,81 255,02 693,2 1884,4 5122,1 13923,0 |
Während also der Reiz, um die Empfindung von 0 bis zum Kardinalwerte oder der natürlichen Fundamentaleinheit wachsen zulassen, bloß um 1,7183 über seinen Schwellenwert 1 zu steigen hat, muß er, um die Empfindung von 9 bis 10 wachsen zu lassen, um 13923 steigen.
Es gibt einen sehr einfachen Fall, auf den man den vorigen Gang in Wirklichkeit beziehen kann. Wenn man sich einem dauernden Geräusche von konstanter Stärke sukzessiv nähert, so werden, wenn dies aus unendlicher Ferne her geschieht, alle Grade des Unbewußtseins von der negativen Unendlichkeit an durchlaufen, bis bei einem gewissen Punkte die Merklichkeit und hiermit der Schwellenwert des Geräusches eintritt, von dem an dann der in der Tabelle verzeichnete Gang der Empfindung in positivem Sinne befolgt wird.
Da die Stärke des Schalles b
in umgekehrtem Verhältnisse des Quadrates der Entfernung steht, so
möge sie 1 bei der Einheit der Entfernung sein, und als diese Einheit
die Entfernung gesetzt werden, wo der Schall eben merklich zu werden beginnt.
Dann ist die Stärke des Schalles ![]() in der Entfernung D. Sei ferner die Einheit der Empfindung beim
Kardinalwerte, so wird der Gang der Empfindung bei natürlichen Logarithmen
durch
in der Entfernung D. Sei ferner die Einheit der Empfindung beim
Kardinalwerte, so wird der Gang der Empfindung bei natürlichen Logarithmen
durch
Man kann in der obigen Tabelle als
eine Eigentümlichkeit bemerken, daß das Verhältnis ![]() bei b = 2 unterhalb des Kardinalpunktes mit
dem Verhältnisse bei 4 oberhalb dieses Punktes ganz übereinstimmt,
nämlich beidesfalls 0,34657 ist, und daß zugleich das Verhältnis
dieser Reize b= 2 und b
= 4, mit dem Verhältnisse der zugehörigen Empfindungen 0,6931
und 1,3863 übereinstimmt.
bei b = 2 unterhalb des Kardinalpunktes mit
dem Verhältnisse bei 4 oberhalb dieses Punktes ganz übereinstimmt,
nämlich beidesfalls 0,34657 ist, und daß zugleich das Verhältnis
dieser Reize b= 2 und b
= 4, mit dem Verhältnisse der zugehörigen Empfindungen 0,6931
und 1,3863 übereinstimmt.
Das Letzte ist eine natürliche Folge des Ersten, denn, wenn
![]()
so ist notwendig zugleich
![]()
Das Erste aber leitet man leicht aus der Maßformel ab.
Wenn nämlich g
= log b , so ist ![]() .
Setzt man nun nach einander b= 2 und
b = 4, so hat man
.
Setzt man nun nach einander b= 2 und
b = 4, so hat man
für b = 2 ×××××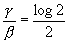
für b = 4 ×××××.
Indem aber log 4 = log 2² = 2 log 2, sind
beide Werte von ![]() identisch.
identisch.
Man kann aber weiter bemerken, daß keineswegs allgemein das Verhältnis der Empfindung mit dem Verhältnisse der zugehörigen fundamentalen Reizwerte übereinstimmt. Dies würde unter Anwendung der Fundamentaleinheiten fordern, daß
![]()
was nicht allgemein statt hat, wenn man für b, b ' beliebige Zahlen setzt. Doch ist das angegebene Gleichheitsverhältnis auch nicht auf jenen einzelnen Fall der fundamentalen Reizwerte 2 und 4 beschränkt, dies vielmehr nur ein besonderer und besonders ausgezeichneter Fall unter unendlich vielen dergleichen Fällen.
Allgemein entspricht jedem gegebenen Werte ![]() oberhalb des Kardinalpunktes ein gleicher unterhalb des Kardinalpunktes,
wie umgekehrt, und allgemein stimmt hier das Verhältnis der fundamentalen
Reizwerte mit dem der Empfindungswerte überein Die so zu einander
gehörigen Werte sollen korrespondierende heißen und die korrespondierenden
fundamentalen Reizwerte insbesondere mit x, y bezeichnet werden.
Es hat einiges Interesse, ihre Verhältnisse festzustellen, sofern
sie zwei Intensitäten bezeichnen, bei denen ein gegebenes Reizquantum
dieselbe Empfindungsleistung gibt, wenn es durch angemessene Verteilung
auf diese Intensitäten gebracht wird. Je weiter beide auseinander
und vom Kardinalwerte abweichen, desto geringer ist die Leistung des Quantums
bei diesen Intensitäten. Im Kardinalwerte selbst treffen beide korrespondierende
Werte in einem gleichen Maximum zusammen.
oberhalb des Kardinalpunktes ein gleicher unterhalb des Kardinalpunktes,
wie umgekehrt, und allgemein stimmt hier das Verhältnis der fundamentalen
Reizwerte mit dem der Empfindungswerte überein Die so zu einander
gehörigen Werte sollen korrespondierende heißen und die korrespondierenden
fundamentalen Reizwerte insbesondere mit x, y bezeichnet werden.
Es hat einiges Interesse, ihre Verhältnisse festzustellen, sofern
sie zwei Intensitäten bezeichnen, bei denen ein gegebenes Reizquantum
dieselbe Empfindungsleistung gibt, wenn es durch angemessene Verteilung
auf diese Intensitäten gebracht wird. Je weiter beide auseinander
und vom Kardinalwerte abweichen, desto geringer ist die Leistung des Quantums
bei diesen Intensitäten. Im Kardinalwerte selbst treffen beide korrespondierende
Werte in einem gleichen Maximum zusammen.
Die Herleitung der Verhältnisse, um die es sich handelt, ist diese:
Wenn x und y die korrespondierenden Reizwerte und g , g ' die zugehörigen Empfindungen sind, so haben wir
![]()
Indem aber g = log x, g' = log y, folgt daraus
![]()
Setzen wir nun ![]() und substituiren yn für x in vorige Gleichung, so erhalten
wir
und substituiren yn für x in vorige Gleichung, so erhalten
wir
n = ![]()
n log y = log ny![]()
log y n = log ny
yn = ny
yn-1 = n
(n-1) log y = log n
![]()
![]()
x = ny = ![]()
Allgemein finden nach vorstehender Herleitung für die korrespondierenden Reizwerte folgende merkwürdige, einander äquivalente, Beziehungen statt:
xy = yx
![]()
![]()
woraus, wenn man ![]() setzt, folgende Bestimmung von x und y fließt:
setzt, folgende Bestimmung von x und y fließt:
![]()
![]()
Gibt man sich also irgend ein beliebiges
Verhältnis ![]() ,
in
welchem die korrespondierenden Reizintensitäten stehen sollen, so
kann man nach vorigen Gleichungen die korrespondierenden Intensitäten
x,
y selbst finden, wobei die Reizeinheit der Schwellenwert, die Empfindungseinheit
beliebig ist.
,
in
welchem die korrespondierenden Reizintensitäten stehen sollen, so
kann man nach vorigen Gleichungen die korrespondierenden Intensitäten
x,
y selbst finden, wobei die Reizeinheit der Schwellenwert, die Empfindungseinheit
beliebig ist.
Hier folgt eine kleine, nach diesen Formeln berechnete, Tabelle, auf deren zweiter Seite die Potenzwerte der ersten Seite in ihre Zahlwerte aufgelöst sind.
|
|
|
|
|
|
| 1 | e | e | 2,718 | 2,718 |
| 2 | 22 | 21 | 4,000 | 2,000 |
| 3 | 33/2 | 3½ | 5,196 | 0,1732 |
| 4 | 44/3 | 41/3 | 6,350 | 0,1582 |
| 5 | 55/4 | 5¼ | 7,477 | 0,1495 |
| 10 | 1010/9 | 101/9 | 12,92 | 0,1291 |
| 100 | 100100/99 | 1001/99 | 104,8 | 1,048 |
Man sieht aus dieser Tabelle, daß, je höher die Intensität des einen korrespondierenden Reizes steigt, um so schwächer die des anderen ist, welche ihm in derselben relativen Empfindungsleistung die Wage hält, so daß z. B. einem Reize, welcher das 104,8-fache seines Schwellenwertes ist, ein Reiz darin korrespondiert, der nur das 1,048 fache seines Schwellenwertes, also 1/100 des vorigen ist, und man mit demselben Reizquantum dieselbe Empfindungsleistung erzielt, wenn man es in dieser oder jener Stärke verwendet, indem die demgemäße Ausbreitung des Reizes den Verlust seiner Intensität ersetzt. Auch hierauf werden uns die späteren Verteilungsformeln der Empfindung auf einem anderen Wege zurückführen.
Man kann nun bemerken, daß die
korrespondierenden fundamentalen Reizwerte 2 und 4, welche den Kardinalwert
e ziemlich in der Mitte haben, und zwischen denen ![]() fast konstant bleibt, also Empfindung und Reiz einander merklich proportional
wachsen, zugleich die einzigen sind, welche in ganzen Zahlen sich ausdrücken,
daß sie die möglichst einfachen Verhältnisse in geraden
Zahlen zum Schwellenwerte 1 darbieten, und der obere das Doppelte und Quadrat
des unteren ist. Sie haben also eine mathematische Auszeichnung vor allen
übrigen, welche mit ihrer realen Bedeutung dahin zusammentrifft, ein
Intervall von sekundärer Bedeutung, nächst dem Hauptintervall
zwischen Schwellenpunkt und Kardinalpunkt, abzugrenzen, das Intervall merklich
proportionalen Fortschrittes von Reiz und Empfindung; welches man das Kardinalintervall
nennen könnte, indes man jenes das Fundamentalintervall nennen mag.
fast konstant bleibt, also Empfindung und Reiz einander merklich proportional
wachsen, zugleich die einzigen sind, welche in ganzen Zahlen sich ausdrücken,
daß sie die möglichst einfachen Verhältnisse in geraden
Zahlen zum Schwellenwerte 1 darbieten, und der obere das Doppelte und Quadrat
des unteren ist. Sie haben also eine mathematische Auszeichnung vor allen
übrigen, welche mit ihrer realen Bedeutung dahin zusammentrifft, ein
Intervall von sekundärer Bedeutung, nächst dem Hauptintervall
zwischen Schwellenpunkt und Kardinalpunkt, abzugrenzen, das Intervall merklich
proportionalen Fortschrittes von Reiz und Empfindung; welches man das Kardinalintervall
nennen könnte, indes man jenes das Fundamentalintervall nennen mag.
Sucht man die mittlere Größe
der Empfindung in diesen zwei Hauptintervallen, so findet man, unter Voraussetzung
des Kardinalwertes der Empfindung als Einheit, als mittlere Empfindung
des Fundamenlalintervalls ![]() =
0,36788, als die des Kardinalintervalls 3 log nat. 2 - 1 = 1,07944. Die
mittlere Empfindung 1 erhält man für das Intervall vom Schwellenwerte
bis zum fundamentalen Reizwerte e2,
und der allgemeine Ausdruck für den Mittelwert einer Empfindung im
Intervall vom fundamentalen Reizwerte x bis y ist
=
0,36788, als die des Kardinalintervalls 3 log nat. 2 - 1 = 1,07944. Die
mittlere Empfindung 1 erhält man für das Intervall vom Schwellenwerte
bis zum fundamentalen Reizwerte e2,
und der allgemeine Ausdruck für den Mittelwert einer Empfindung im
Intervall vom fundamentalen Reizwerte x bis y ist
![]() .
.
Der Mittelwert der Empfindung in dem Intervall zwischen zwei Reizwerten x, y kann nämlich unter der Voraussetzung von k = 1, b = 1 durch
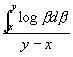
dargestellt werden; welcher Wert durch Integration zu obigen Bestimmungen führt.
Auf der zweiten Seite der Tabelle (s. o.) ist, abgesehen von den einschaltungsweise zugefügten Empfindungswerten 1,5 und 2,7183, die Reihe der Empfindungen als eine arithmetische mit der Differenz 1 dargestellt. Man sieht, daß ihr eine geometrische der Reizwerte entspricht, indem jeder folgende Reizwert aus dem früheren durch Multiplikation mit dem Exponenten e = 2,7183 hervorgeht.
Dieses Resultat des Zusammengehörens der arithmetischen Empfindungsreihe und geometrischen Reizreihe ist nicht an die besonderen Einheiten geknüpft, die hier gewählt sind; sondern allgemein entspricht jeder arithmetischen Reihe von Empfindungen, auch bei anderen Einheiten und anderer Differenz, eine geometrische der Reizwerte. Und zwar ist der Exponent einer Empfindungsreihe mit der Differenz 1 allgemein gleich dem fundamentalen Reizwerte, bei dem man die Einheit der Empfindung setzt, im Falle unserer Tabelle e, bei irgend einer anderen Differenz aber gleich der Potenz dieses fundamentalen Reizwertes, welcher durch die Differenz bezeichnet wird. So hat man nach unserer Tabelle für die Reihe der Empfindungen 1,3,5..., wo die Differenz 2 ist, eine geometrische Reihe der Reize mit dem Exponenten e2.
Man kann die Maßformel noch unter einer etwas anderen Form, als früher nach der Betrachtung aufstellen, daß sich der Reiz b als aus einem der Schwelle gleichen Teile b und einem positiven oder negativen Zuwachse a dazu, je nachdem der Reiz über oder unter dem Schwellenwerte ist, bestehend ansehen, also b = b + a setzen läßt, wodurch die Maßformel übergeht in
![]() .
.
So stellt sich g als Funktion des Verhältnisses dar, welches der Zuwachs zur Schwelle gegen die Schwelle hat, indes die frühere Form g als Funktion des Verhältnisses gab, welches der gegebene Reiz zur Schwelle hat.
Die jetzige Form zeigt sich bequem, folgende Resultate abzuleiten.
So lange der Reiz den Schwellenwert
nur sehr wenig übersteigt, also ![]() ein sehr kleiner Bruch ist, klein genug, daß die höheren Potenzen
gegen die erste zu vernachlässigen, kann man nach Kap. 14 für
log
ein sehr kleiner Bruch ist, klein genug, daß die höheren Potenzen
gegen die erste zu vernachlässigen, kann man nach Kap. 14 für
log![]() substituieren
M
substituieren
M![]() , wo
M
der Modulus. Wonach eine Empfindung, so lange sie sehr schwach ist, im
direkten Verhältnisse von
, wo
M
der Modulus. Wonach eine Empfindung, so lange sie sehr schwach ist, im
direkten Verhältnisse von![]() steht und steigt. Ist hingegen der Reiz so groß, daß 1 gegen
steht und steigt. Ist hingegen der Reiz so groß, daß 1 gegen ![]() zu vernachlässigen, so steigt die Empfindung proportional mit log
zu vernachlässigen, so steigt die Empfindung proportional mit log ![]() = log a - log b, und ist sie endlich so groß, daß
auch log b gegen log a zu vernachlässigen, so steigt
sie proportional mit log a, und wird unabhängig vom Schwellenwerte.
= log a - log b, und ist sie endlich so groß, daß
auch log b gegen log a zu vernachlässigen, so steigt
sie proportional mit log a, und wird unabhängig vom Schwellenwerte.
Die Weise, wie nach der Maßformel mit dem Wachstume des Reizes die Empfindung steigt, kann leicht graphisch durch die logarithmische Kurve repräsentiert werden, indem man die Größe des Reizes durch Abszissen, die zugehörigen Werte der Empfindung durch darauf rechtwinklige Ordinaten darstellt.