![]()
Die im Eingange des vorigen Kapitels entwickelte Fundamentalformel
![]()
stützt sich auf Versuche über Unterschiede, welche an der Grenze des Merklichen stehen. Hiernach können dy und dß in ihr als Differenziale betrachtet und behandelt werden. Durch Integration derselben findet man dann zunächst unter Voraussetzung natürlicher Logarithmen
o = K log b + C,
mithin
C = - K log b
und
g = K(log b- log b).
Da ein gewöhnlicher Logarithmus gleich dem, mit dem
Modulus M = 0,4342945 multiplizierten natürlichen Logarithmus
ist, so geht, unter Anwendung gewöhnlicher Logarithmen und Setzung
von ![]() , die
vorige Formel über in
, die
vorige Formel über in
g= k (log b
- log b) = k log ![]() .
.
Diese Herleitung würde illusorisch werden, wenn die Tatsache der Schwelle nicht bestände, welche daher mit dem Weber’schen Gesetze zusammen erst die zulängliche Unterlage der Maßformel und hiermit des absoluten Empfindungsmaßes bildet. In der Tat, sollte die Empfindung statt bei einem endlichen Werte vielmehr bei einem Nullwerte des Reizes erlöschen, so würden wir für die Konstante C einen negativ unendlichen Wert erhalten, und es wäre kein endlicher Ausdruck für einen absoluten Empfindungswert zu finden; doch würde nichts hindern, Empfindungsunterschiede noch zu messen, in deren Ausdruck C verschwindet. Euler’s Formel für Tonhöhen, und Steinheil’s Formel für Sterngrößen, als auf der Tatsache der Schwelle nicht mit fußend, beziehen sich daher auch nur auf Empfindungsunterschiede.
Auch ohne Infinitesimalrechnung kann man die Maßformel aus dem Weber’schen Gesetze unter Zuziehung der Tatsache der Schwelle ableiten; wenn man das Weber’sche Gesetz so ausdrückt, daß der Empfindungsunterschied derselbe bleibt, wenn das Reizverhältnis dasselbe bleibt. Und es verdient diese Ableitung namentlich insofern Beachtung, als sie in den Stand setzt, den bisherigen Gang umzukehren, d. h. statt von den Erfahrungsdaten aus erst zur Fundamentalformel zu gelangen, um daraus in vorhin angegebener Weise die Maßformel durch Integration abzuleiten, vielmehr erst zur Maßformel zu gelangen, um daraus die Fundamentalformel durch Differenzierung abzuleiten.
In der Tat, seien g
und g' zwei Empfindungen, welche respektiv
den Reizen b und b'
zugehören, so sagt das Weber’sche Gesetz in der letztbemerkten Form,
daß g- g
' konstant bleibt, so lange ![]() konstant bleibt, oder daß
konstant bleibt, oder daß
Ohne Zuziehung der Tatsache der Schwelle könnte nun die Funktion f beliebig genommen werden, die Bedingung des Weber’schen Gesetzes würde immer erfüllt sein. In der Tat würden folgende Formeln
g - g¢
= ![]()
= 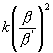
= 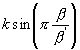 etc.
etc.
gleich gut die Bedingung erfüllen, daß g
-
g ' konstant bleibt, so lange ![]() konstant bleibt, als die Formel
konstant bleibt, als die Formel
In der Tat, setzen wir in der Gleichung
g = ![]() .
.
Entsprechend erhalten wir aus der Gleichung
g ¢
- g = ![]()
dadurch, daß wir g= 0 bei dem Werthe b = b setzen,
g¢ = ![]() .
.
Dies gibt den Unterschied
g - g¢
= ![]() -
- ![]() ,
,
welcher Unterschied dem anfänglich gefundenen
g - g¢
= ![]()
gleich sein muß. D. h. man muß haben
![]() =
= ![]() -
- ![]()
oder
Substituiert man in vorigen Gleichungen ![]() für x,
für x, ![]() für y, mithin das Produkt beider
für y, mithin das Produkt beider ![]() für xy, so wird sie mit der obigen identisch, und es folgt
daraus, daß man zu setzen hat
für xy, so wird sie mit der obigen identisch, und es folgt
daraus, daß man zu setzen hat
![]() ;
; 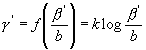 .
.
Sollten jedoch b, b
' mit g , g ¢
zugleich Null werden, also b = 0 sein, so würde diese Ableitung
wegen der unendlichen Werte, welche log ![]() ,
log
,
log ![]() annehmen,
nicht stattfinden und die Funktion f würde beliebig genommen
werden können.
annehmen,
nicht stattfinden und die Funktion f würde beliebig genommen
werden können.
Die logarithmische Funktion des Reizverhältnisses, auf die wir uns so mit Notwendigkeit gewiesen finden, zeichnet sich außerdem vor allen anderen Funktionen des Reizverhältnisses, die man etwa versuchen könnte, derselben zu substituieren, durch eine Eigenschaft aus, die, insoweit sie sich durch Erfahrung konstatieren läßt, nicht minder als die Bedingung der Schwelle dienen kann, durch Zutritt zu dem Weber’schen Gesetze die logarithmische Funktion sicher zu begründen; und ohne welche ebensowenig eine Rechnung mit Empfindungsgrößen auf Grund des Weber’schen Gesetzes stattfinden könnte, als ohne die vorige; indem das mathematische Axiom, daß man durch Summierung zweier Unterschiede etwas dem Totalunterschiede Gleiches erhält, nur eben mittelst der logarithmischen Funktion des Reizverhältnisses für Empfindungsunterschiede bestehen kann, sofern sie überhaupt Funktionen des Reizverhältnisses sind.
Seien z. B, drei Reize in absteigender Ordnung der Größen b, b ', b " mit den zugehörigen Empfindungen g , g¢ , g" gegeben, so würde nach keiner, als unserer logarithmischen Funktion des Reizverhältnisses der Unterschied, den wir zwischen den extremen Empfindungen g und g" finden, gleich der Summe der Unterschiede ausfallen, die wir zwischen g und g' , g ' und g" finden.
Erläutern wir es an Sterngrößen. Die drei Reize b, b ' b " sollen durch drei Sterngrößen l., 2., 3. Klasse repräsentiert werden. Ist der Empfindungsunterschied irgend eine andere Funktion des Reizverhältnisses, als unsere logarithmische, so muß der Unterschied der Helligkeit, den man findet, wenn man mit dem Auge von der 1. zur 3. Größe direkt übergeht, größer oder kleiner erscheinen, als der Unterschied der Helligkeit, den man findet, wenn man von der 1. zur 2. übergeht, plus dem Unterschiede, den man findet, wenn man von der 2. zur 3. übergeht, und es lassen sich zwischen die ganzen Größen keine Bruchgrößen einschieben, deren Differenzen von den ganzen Nachbargrößen die Totaldifferenz derselben wiedergäben. Da aber die Astronomen wirklich Bruchgrößen nach diesem Prinzipe auf das Urteil des Auges hin einschieben, so muß das betreffende Axiom hier seine Gültigkeit haben. Desgleichen könnte uns das Intervall der Oktave nicht eben so groß als die Summe von Quinte und Quarte erscheinen, was aber eine Erfahrungstatsache ist. Und wenn man sich vielleicht auch nicht getraut, diese Gleichheit des Totalunterschiedes der Empfindung mit der Summe der partiellen Empfindungen im Gebiete anderer Empfindungen eben so entschieden als Resultat der Erfahrung auszusprechen, als im Gebiete der Tonhöhen, so wird man immerhin zugestehen, daß noch weniger ein Grund in der Erfahrung für das Gegenteil vorliegt, ja es möchten ohnedem Widersprüche und Inkongruenzen im Empfindungsgebiete eintreten, wovon sich nichts zeigt.
Man kann sich nun zuvörderst erst empirisch überzeugen, daß, wenn g , g ', g " die drei Empfindungen sind, welche den drei Reizen b, b ', b " zugehören, nach keiner der oben aufgestellten Funktionen als der logarithmischen g - g " gleich (g - g') + (g¢ - g '') erhalten wird. Gesetzt, es gälte die erste Form, so würde man haben
![]()
![]()
Sollte nun g - g " = (g - g') + (g ' - g ")sein, so müßte
![]()
sein, also
![]() oder =
oder = ![]()
welches nicht allgemein, sondern nur unter der ganz partikulären
Voraussetzung, daß ![]() der Fall sein könnte. Nicht minder würde man Ungleichungen für
alle anderen Funktionen finden; mit Ausnahme der logarithmischen. In der
Tat, nach dieser hat man
der Fall sein könnte. Nicht minder würde man Ungleichungen für
alle anderen Funktionen finden; mit Ausnahme der logarithmischen. In der
Tat, nach dieser hat man
![]()

Gleichwertigkeit zwischen
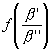 ;
g - g² =
;
g - g² = 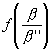
![]() +
+ 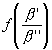 =
= 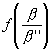
sein, welcher Gleichung mit Rücksicht darauf, daß ![]() =
= ![]() ×
×![]() ist, nach dem, was (s. o.) bemerkt ist, nicht anders entsprochen werden
kann, als wenn man setzt
ist, nach dem, was (s. o.) bemerkt ist, nicht anders entsprochen werden
kann, als wenn man setzt
![]() = k log
= k log ![]() .
.
Eben so, wie es Bedingungen gibt, welche entschieden nötigen, bei der logarithmischen Funktion stehen zu bleiben, so gibt es solche, durch welche diese oder jene der Funktionen, welche oben angeführt sind, entschieden ausgeschlossen wird. Sollte die Funktion diese Form haben
g - g
' = k![]()
so müßte ein Empfindungsunterschied nicht nur immer gleich groß sein, wenn das Reizverhältnis gleich groß ist, sondern auch in demselben Verhältnisse wachsen, als das Reizverhältnis wächst, unabhängig von der Größe der Reize. Dem aber widerspricht die Erfahrung. Denn z. B. bei den Sterngrößen entspricht die Verdoppelung des Unterschiedes zweier aufeinander folgender Sterngrößen, oder der Unterschied einer Sterngröße von der je dritten keineswegs einer Verdoppelung des Verhältnisses der Lichtintensitäten, welche den aufeinander folgenden Sterngrößen zugehören. Sollte anderseits die Form diese sein
g - g
' = k sin![]()
so müßte der Empfindungsunterschied mit steigender Intensität des einen Reizes, während der andere unverändert bleibt, periodisch zu- und abnehmen, was ebenfalls nicht der Fall.