Ohne noch ein Maß der Empfindung zu haben, kann man doch den durch das Weber’sche Gesetz ausgesprochenen Fall, daß der Empfindungsunterschied sich gleich bleibt, wenn der relative Reizunterschied sich gleich bleibt, und den durch das mathematische Hilfsprinzip begründeten Satz, daß kleine Empfindungszuwüchse den Reizzuwüchsen proportional gehen, in Verbindung durch einen scharfen mathematischen Ausdruck darstellen.
Nehmen wir an, wie es bei den Versuchen
zur Bewährung des Weber’schen Gesetzes im Allgemeinen der Fall, daß
der Unterschied zweier Reize, oder, was dasselbe sagt, der Zuwuchs zum
einen Reize sehr klein im Verhältnisse zu diesem sei. Der Reiz, zu
welchem der Zuwuchs erfolgt, heiße b ,
der kleine Zuwuchs heiße db , wo
man den Buchstaben d nicht als eine besondere Größe,
sondern bloß als Zeichen zu betrachten hat, daß dbein
kleiner Zuwuchs zu b sei; schon jetzt kann man
an das Differenzialzeichen dabei denken. So ist der relative Reizzuwuchs ![]() .
Die Empfindung anderseits, die von dem Reize b
abhängt, heiße g, der kleine
Zuwuchs der Empfindung, welcher bei Wachstum des Reizes um db
entsteht,
heiße dg , wo d wieder nur
als Zeichen kleinen Zuwuchses zu verstehen. db
und
dg sind jede auf eine Einheit ihrer Art,
die willkürlich ist, bezogen zu denken.
.
Die Empfindung anderseits, die von dem Reize b
abhängt, heiße g, der kleine
Zuwuchs der Empfindung, welcher bei Wachstum des Reizes um db
entsteht,
heiße dg , wo d wieder nur
als Zeichen kleinen Zuwuchses zu verstehen. db
und
dg sind jede auf eine Einheit ihrer Art,
die willkürlich ist, bezogen zu denken.
![]() (1)
(1)
wo K eine (von den für g
und b zu wählenden Einheiten abhängige)
Konstante ist. In der Tat, man multipliziere db
und
b beide mit beliebigen, nur immer beide mit
denselben Zahlen, so bleibt das Verhältnis ungeändert, mithin
auch der Empfindungsunterschied dg konstant.
Dies ist das Weber’sche Gesetz. Man verdoppele, verdreifache den Wert der
Änderung
db allein, ohne den Ausgangswert
b
zu ändern, so nimmt auch die Änderung
dg
den doppelten, dreifachen Wert an. Dies ist das mathematische
Prinzip. Die Gleichung ![]() genügt also vollständig zugleich jenem Gesetze und diesem Prinzipe;
und zwar genügt keine andere Gleichung beiden zusammen. Sie soll die
Fundamentalformel heißen, indem die Ableitung aller weiter folgenden
Formeln auf ihr beruhen wird.
genügt also vollständig zugleich jenem Gesetze und diesem Prinzipe;
und zwar genügt keine andere Gleichung beiden zusammen. Sie soll die
Fundamentalformel heißen, indem die Ableitung aller weiter folgenden
Formeln auf ihr beruhen wird.
Die Fundamentalformel setzt noch kein Maß der Empfindung voraus, gewährt aber auch kein solches, sondern drückt bloß die gesetzliche Beziehung aus, welche zwischen kleinen relativen Reizzuwüchsen und Empfindungszuwüchsen statt hat. Sie ist mit einem Worte nichts Anderes, als der in Eins gefaßte Ausdruck des Weber’schen Gesetzes und des mathematischen Hilfsprinzips durch mathematische Zeichen.
Es hängt aber mit dieser Formel durch infinitesimale Summation eine andere zusammen, welche eine allgemeine Größenbeziehung zwischen der, aus Reizzuwüchsen summierten, Reizgröße und der, aus Empfindungszuwüchsen summierten, Empfindungsgröße aufstellt, in der Art, daß mit der Richtigkeit der ersten Formel unter Mitvoraussetzung der Tatsache der Schwelle solidarisch zugleich die Richtigkeit der letzten gegeben ist.
Vorbehaltlich der späteren genaueren Herleitung suche ich zuvörderst den Zusammenhang beider Formeln wie folgt in allgemeiner Weise verständlich zu machen.
Leicht kann man bemerken, daß die Beziehung zwischen den Zuwüchsen dg und db in der Fundamentalformel der Beziehung zwischen den Zuwüchsen eines Logarithmus und den Zuwüchsen der zugehörigen Zahl entspricht. Denn, wie man sich leicht, sei es aus der Theorie oder aus den Tafeln, überzeugen kann, so wachsen die Logarithmen um gleich viel, nicht, wenn die zugehörigen Zahlen um gleich viel wachsen, sondern wenn dieselben um einen gleichen Verhältnisteil wachsen; mit anderen Worten, die Zuwüchse der Logarithmen bleiben gleich groß, wenn die relativen Zahlenzuwüchse gleich groß bleiben. So gehören z. B. folgende Zahlen und Logarithmen zusammen:
10
1,000000
11
1,0413927
100
2,000000
110
2,0413927
1000
3,000000
1100
3,04l3927
Nicht minder macht sich in der Beziehung zwischen Logarithmus und Zahl ganz eben so die Tatsache der Schwelle geltend, als in der Beziehung zwischen Empfindung und Reiz. Die Empfindung beginnt mit Werten, die den Nullwert übersteigen, nicht bei dem Nullwerte, sondern bei einem endlichen Werte des Reizes, dem Schwellenwerte, und so beginnt ein Logarithmus mit Werten, die den Nullwert übersteigen, nicht bei dem Nullwerte der Zahlen, sondern bei einem endlichen Werte der Zahlen, dem Werte 1, sofern der Logarithmus von l gleich Null ist.
Stehen nun nach Vorigem die Zuwüchse von Empfindung und Reiz in einem entsprechenden Verhältnisse, als die von Logarithmus und Zahl, steht auch der Punkt, von dem an die Empfindung merkliche Werte anzunehmen beginnt, in einer entsprechenden Beziehung zum Reize, als der Punkt, von dem an die Logarithmen positive Werte erlangen, zur Zahl, so wird man erwarten dürfen, daß auch Empfindung und Reiz selbst in einem entsprechenden Verhältnisse stehen, als Logarithmus und Zahl, welche wie jene als aus sukzessiven Zuwüchsen summiert betrachtet werden können.
Hiernach wäre die einfachste Beziehung zwischen beiden, die wir aufstellen können,
g = log b.
In der Tat wird sich bald zeigen lassen, daß unter Wahl angemessener Einheiten von Reiz und Empfindung die funktionelle Beziehung zwischen beiden auf diese einfachste Form zurückkommt. Inzwischen ist sie nicht die allgemeinste, die sich aufstellen läßt, sondern eben nur unter Voraussetzung bestimmter Einheiten von Empfindung und Reiz, wovon später, gültig, und für die vorige indirekte und nicht strenge Ableitung eine direkte und strenge zu verlangen.
Der Sachverständige übersieht sofort, wie diese zu bewirken ist, indem man nämlich die Fundamentalformel als Differenzialformel behandelt und integriert. Im folgenden Kapitel findet man dies ausgeführt; hier sei es als geschehen vorausgesetzt, und an Denjenigen, welcher einer einfachen infinitesimalen Ableitung nicht zu folgen vermag, der Anspruch gemacht, das Resultat als mathematische Tatsache anzunehmen. Dies Resultat ist folgende Funktionsformel zwischen Reiz und Empfindung, welche den Namen Maßformel führen und jetzt weiter diskutiert werden soll:
g = k( log b - log b) (2).
In dieser Formel bedeutet k wiederum eine, von den gewählten Einheiten und zugleich vom logarithmischen Systeme abhängige, Konstante, und b eine zweite Konstante, welche den Schwellenwert des Reizes b bezeichnet, bei dem die Empfindung g beginnt und schwindet.
Nach der im folgenden Kapitel gegebenen
Ableitungsweise der Formel fällt die Konstante k mit der Konstante
K
der Fundamentalformel zusammen, wenn man sich natürlicher Logarithmen
bedient; indes bei Anwendung gewöhnlicher Logarithmen ![]() und
K
= kM ist, wo M der Modulus des gemeinen logarithmischen Systemes
in der bereits angegebenen Bedeutung ist.
und
K
= kM ist, wo M der Modulus des gemeinen logarithmischen Systemes
in der bereits angegebenen Bedeutung ist.
Nach dem Satze, daß für den Unterschied der Logarithmen zweier Zahlen der Logarithmus ihres Quotienten substituierbar ist (vgl. Kap. 14), kann man für obige Form der Maßformel auch folgende, zumeist für Ableitung von Folgerungen bequemere, substituieren
In Worte übersetzt, lautet die Maßformel:
Die Größe der Empfindung (g ) steht im Verhältnisse nicht zu der absoluten Größe des Reizes (b ), sondern zu dem Logarithmus der Größe des Reizes, wenn dieser auf seinen Schwellenwert (b), d. i. diejenige Größe als Einheit bezogen wird, bei welcher die Empfindung entsteht und verschwindet, oder kurz, sie ist proportional dem Logarithmus des fundamentalen Reizwertes.
Beeilen wir uns, bevor wir weiter vorschreiten, zu zeigen, daß die Maßformel diejenigen Beziehungen zwischen Reiz und Empfindung, aus denen sie abgeleitet ist, auch richtig als Folgerungen wiedergibt, und also rückwärts in denselben ihre Bewährung findet, sofern sie sich in der Erfahrung bestätigen. Wir erhalten darin zugleich die einfachsten Beispiele der Anwendung der Maßformel.
Die Maßformel ist begründet auf das Weber’sche Gesetz und die Tatsache der Reizschwelle; und beides muß also auch wieder aus ihr fließen.
Was nun das Weber’sche Gesetz anlangt, so läßt es sich unter der Form, daß gleiche Empfindungszuwüchse gleichen relativen Reizzuwüchsen zugehören, durch die Differenzierung der Maßformel gewinnen, sofern man dadurch auf die Fundamentalformel zurückkommt, welche den Ausdruck des Gesetzes in dieser Form enthält.
In der anderen Form, daß gleiche Empfindungsunterschiede gleichen Reizverhältnissen zugehören, läßt es sich ganz elementar wie folgt ableiten.
Seien zwei Empfindungen, deren Unterschied es zu betrachten gilt, g und g ', und die ihnen zugehörigen Reize b und b'. Dann haben wir nach der Maßformel
g ' = k (logb' - log b)
In einem späteren Kapitel werden wir auf vorstehende Formel, als eine der einfachsten Folgerungen der Maßformel, unter dem Namen der Unterschiedsformel zurückkommen.
Was die Tatsache der Schwelle anlangt,
welche darin ruht, daß die Empfindung nicht bei einem Nullwerte,
sondern endlichen Werte des Reizes ihren Nullwert hat, von wo an sie mit
steigendem Reizwerte erst merkliche Werte anzunehmen beginnt, so liegt
sie insofern in der Maßformel enthalten, als g
den Wert Null nach der Maßformel nicht annimmt, wenn b=
0, sondern wenn b gleich dem endlichen Werte
b
ist, wie sich sowohl aus der Form (2) als (3) der Maßformel ergibt,
aus (2) unmittelbar, aus (3) mit Rücksicht, daß, wenn
b
gleich b wird, log![]() =
log1 wird, und log1 = 0 ist.
=
log1 wird, und log1 = 0 ist.
Natürlich werden nun auch alle Folgerungen des Weber’schen Gesetzes und der Tatsache der Schwelle zugleich Folgerungen unserer Maßformel.
Aus ersterem Gesetze fließt, daß jeder gegebene Zuwachs eines Reizes nach Maßgabe weniger Zuwachs der Empfindung gibt, als der Reiz, dem er zuwächst, größer ist, und bei hohen Reizgraden gar nicht mehr erheblich empfunden wird, indes er bei niederen ausnehmend erheblich erscheinen kann.
In der Tat führt der Zuwachs einer großen Zahl b durch eine gegebene Größe nur einen ohne Vergleich kleineren Zuwachs im zugehörigen Logarithmus g mit, als die Vermehrung einer kleinen Zahl b um denselben Zuwachs. Wenn die Zahl 10 um 10 wächst, also auf 20 steigt, so wächst der zu 10 gehörige Logarithmus 1 auf 1,3010. Wenn aber die Zahl 1000 um 10 wächst, so wächst der zu 1000 gehörige Logarithmus 3 nur auf 3,0043. Erstenfalls hat sich der Logarithmus um etwa 1/3, letzterenfalls nur etwa um 1/700 seiner Größe vermehrt.
Mit der Tatsache der Schwelle hängt die Folgerung zusammen, daß eine Empfindung um so weiter von der Merklichkeit entfernt bleibt, je mehr der Reiz unter seinen Schwellenwert sinkt. Diese Entfernung der Empfindung von der Merklichkeit oder diese Tiefe derselben unter der Schwelle wird nach unserer Maßformel eben so durch negative Werte von g repräsentiert, wie die Erhebung über dieselbe durch positive.
In der Tat übersieht man aus der
Form (2) unmittelbar, daß, wenn b kleiner
als b und mithin log b kleiner als log
b
wird, die Empfindung g negative Werte annimmt;
und dasselbe fließt aus der Form (3) nach der Betrachtung, daß ![]() zu einem echten Bruche wird, wenn b< b;
der Logarithmus eines echten Bruches aber negativ ist.
zu einem echten Bruche wird, wenn b< b;
der Logarithmus eines echten Bruches aber negativ ist.
Insofern wir Empfindungen, welche zwar von einem Reize angeregt sind, aber nicht hinreichend, um das Bewußtsein zu affizieren, kurz unbewußte, diejenigen, welche es affizieren, bewußte nennen, werden also die unbewußten Empfindungen durch negative, die bewußten durch positive Werte in unserer Formel repräsentiert. Auf diese Repräsentation werden wir wegen ihrer besonderen Wichtigkeit, und vielleicht nicht jedem unmittelbar einleuchtenden Triftigkeit noch in einem besonderen Kapitel (Kap. 18) zurückkommen. Für jetzt will ich mich nicht weiter dabei aufhalten.
Unsere Maßformel entspricht nach Vorstehendem der Erfahrung :
1) In den Gleichheitsfällen, wo ein Empfindungsunterschied bei Änderung der absoluten Stärke der Reize sich gleich bleibt (Weber’sches Gesetz).
2) In den Grenzfällen, wo die Empfindung selbst, und wo ihre Änderung bemerklich oder erheblich zu sein aufhört, Ersteres, wenn sie auf die Schwelle tritt, Letzteres, wenn sie so hoch gestiegen ist, daß ein gegebener Reizzuwachs nicht mehr erheblich gespürt wird.
3) In den Gegensatzfällen zwischen Empfindungen, welche die Merklichkeit übersteigen und welche die Merklichkeit nicht erreichen, kurz bewußten und unbewußten Empfindungen.
Hiernach dürfte sie als wohlbegründet anzusehen sein.
Für den ersten Anblick könnte man geneigt sein, zu glauben, nicht bloß die Tatsache der Reizschwelle, sondern auch der Unterschiedsschwelle müsse sich aus der Maßformel folgern lassen, weil diese darauf gegründet sei. In der Tat ist das Weber’sche Gesetz und hiermit die Hauptunterlage der Maßformel großenteils nach der Methode der eben merklichen Unterschiede aus Versuchen über das Gleichbleiben eines eben merklichen Empfindungsunterschiedes, welcher mit der Unterschiedsschwelle zusammenhängt und nahe zusammenfällt, gefolgert. Aber, sehen wir näher zu, so ist es nur die gleiche Größe dieses Unterschiedes bei gleichem relativen Reizunterschiede, nicht, daß die Merklichkeit erst bei einem endlichen Werte dieses Reizunterschiedes eintritt, was zur Begründung der Fundamentalformel und hiermit Maßformel gebraucht wird; daher auch der nur eben merkliche Unterschied bei dieser Begründung eben so gut durch einen durchschnittlich größeren, als den eben merklichen, wie bei der Methode der richtigen und falschen Fälle, oder einen durchschnittlich kleineren, wie bei der Methode der mittleren Fehler, vertreten werden kann, insofern er eine Beurteilung der Gleichheit zuläßt. Von der anderen Seite tritt aber auch die Tatsache der Unterschiedsschwelle, richtig aufgefaßt, nicht in Widerspruch mit der Maßformel, sondern führt erforderlich berücksichtigt und in einen mathematischen Ausdruck aufgenommen, zu einer allgemeineren Formel (Unterschiedsmaßformel), deren Begründung und Diskussion einem späteren Kapitel vorbehalten bleibt, einer Formel, welche für besonders aufgefaßte (sog. empfundene) Unterschiede zwischen Empfindungen dasselbe leistet, als die Maßformel für absolute Empfindungen und deren Differenzen.
Das Parallelgesetz, nach welchem ein Empfindungsunterschied sich gleich bleibt, wenn sich die Reizbarkeit und hiermit der Schwellenwert b für die verschiedenen Reize in demselben Verhältnisse ändert, ist eine Folgerung unserer Formel, wenn k dabei konstant bleibt, nur daß nach einem richtigen Gange die Konstanz von k hierbei selbst erst umgekehrt aus dem Parallelgesetze gefolgert werden kann, wie unten gezeigt wird.
Mit der Maßformel hat man nun ein allgemeines, nicht mehr bloß für Gleichheitsfälle der Empfindung gültiges, Abhängigkeitsverhältnis zwischen der Größe des fundamentalen Reizwertes und der Größe der zugehörigen Empfindung gewonnen, welches gestattet, aus Größenverhältnissen des ersten das Wievielmal des letzten zu berechnen, womit das Maß der Empfindung gegeben ist.
Eine n-mal so starke Empfindung g wird hiernach nicht die sein, welche einem n-mal so großen Werte des äußeren oder äquivalenten inneren Reizes b zugehört, sondern welche einem solchen Werte von b zugehört, der nach der Maßformel einen n-mal so großen Wert von g gibt.
Gesetzt, die Empfindung g
bei einem bestimmten Fundamentalwerte des Reizes ist gegeben, so wird g
auf den n-fachen Wert steigen, wenn der fundamentale Reizwert ![]() auf die n-fache Potenz steigt, und auf
auf die n-fache Potenz steigt, und auf ![]() ihres Wertes herabkommen, wenn aus dem fundamentalen Reizwerte die n-te
Wurzel gezogen wird.
ihres Wertes herabkommen, wenn aus dem fundamentalen Reizwerte die n-te
Wurzel gezogen wird.
Denn, was das Erste anlangt, so hat man, indem man auf beiden Seiten der Maßformel mit n multipliziert
![]()
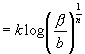 (6)
(6)
![]()
sofern bekanntlich allgemein ![]() .
.
Überhaupt aber ist das Verhältnis zweier Empfindungen g, g ', die den Reizen b, b ' zugehören:
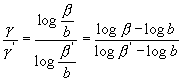 (7)
(7)
also gleich dem Verhältnisse der Logarithmen der fundamentalen Reizwerte.
In der Maßformel und ihren Ableitungen ist sowohl die Größe des Reizes als der Empfindung jede auf eine Einheit ihrer Art zu beziehen. Denn da Reiz und Empfindung ganz heterogener Natur sind, so können sie auch nur durch Einheiten ihrer Art besonders gemessen, nicht aber ihnen eine gemeinsame Einheit untergelegt werden. In der Tat erklären wir in unserem Maße der Empfindung diese nicht als ein Wievielmal des Reizes, sondern als ein Wievielmal einer als Einheit untergelegten Empfindungsgröße derselben Art, und nur die Beziehung der Empfindung zu ihrer Einheit wird nach der Beziehung des Reizes zu seiner Einheit bestimmt, indem beide Beziehungen eine Funktion von einander sind, welche derartig ist, daß, wenn die eine Beziehung gegeben ist, die andere daraus zu folgern ist. Diese Funktion ist es, die durch unsere Maßformel dargestellt wird.
Bei der an sich willkürlichen Wahl der Einheiten von Reiz und Empfindung können verschiedene Rücksichten bestimmen. Man kann die Einheiten von Reiz und Empfindung zusammentreffen lassen, d. h. die Einheit der Empfindung bei dem Reizwerte annehmen, den man als Einheit des Reizes annimmt, kann sie aber auch eben so gut auseinanderfallen lassen, d. h. die Einheit der Empfindung bei einem anderen Reizwerte als der Reizeinheit annehmen, da gar keine Notwendigkeit vorliegt, beide zusammentreffen zu lassen. Es ändern sich nur mit jeder anderen Wahl der Einheiten die Konstanten der Formel und hiermit die absolute Größe der Zahl, durch welche eine Empfindungsgröße ausgedrückt wird, ohne daß aber die Größenverhältnisse der Empfindung, auf die es beim Maße allein ankommt, andere dadurch werden.
Verlangt man die einfachstmögliche Form der Maßformel
Daß k = 1 wird,
wenn man die Empfindungseinheit bei einem fundamentalen Reizwerte gleich
der Grundzahl der angewandten Logarithmen setzt, findet sich leicht so:
Sei allgemein die, in irgend einem Systeme genommene, Grundzahl a, so
hat man, indem man die Empfindungseinheit bei ![]() setzt, also hierbei g = 1 setzt, nach Substitution
dieser Werte in die Massformel
setzt, also hierbei g = 1 setzt, nach Substitution
dieser Werte in die Massformel
1 = k log a
mithin
![]()
Da nun in jedem Systeme der Logarithmus der Grundzahl also log a = 1 ist, so erhält hierdurch k den Wert 1.
Diese Einheiten von Reiz und Empfindung, welche b = l und k = 1 machen und hiermit auf die einfachstmögliche Form der Maßformel g = log b zurückführen, sollen künftig die Fundamentaleinheiten heißen, und zwar gewöhnliche oder natürliche, je nachdem man dabei gewöhnliche oder natürliche Logarithmen voraussetzt. Die Reizeinheit bleibt beidesfalls dieselbe; aber die Empfindungseinheit ändert sich nach dem logarithmischen Systeme im Verhältnisse von 10 : 2,718 ....
Unter Voraussetzung der Fundamentaleinheiten kann man einfach sagen, die Stärke der Empfindung sei der Logarithmus der Stärke des Reizes, und man wird zwar je nach dem angewandten logarithmischen Systeme den Zahlausdruck für die Größe der Empfindung verschieden, die absolute Größe aber in Rücksicht der dabei unterliegenden verschiedenen Einheit gleich groß finden, wie man ja auch für die Länge 1 die Länge 12 setzen kann und mit der letzteren Zahl keine größere Länge bezeichnen wird, als mit der ersteren, wenn man unter 12 zwölf Zolle und unter 1 einen Fuß versteht.
Hiernach wird z. B. unter Anwendung gewöhnlicher Fundamentaleinheiten eine Verdoppelung der Empfindung 1 stattfinden, wenn der Reiz sich verzehnfacht, da log 10 = 1, log 100 = 2. Aber man würde Unrecht haben, zu sagen, daß überhaupt jede Empfindung sich verdoppelt, wenn sich der Reiz verzehnfacht, sondern eben nur jene Empfindung 1, die dem Werte b = 10 zugehört, d. i. einem Reize, der 10 mal so groß als sein Schwellenwert ist. Sollte die Empfindung 2 sich verdoppeln, welche zum Reize 100 gehört, so würde dies bei einem Reize stattfinden, dessen Logarithmus 4 ist, d. i. bei 10000, also hier der Reiz sich nicht verzehnfachen, sondern verhundertfachen müssen, u. s. f.
Auch wird, wenn die Empfindung 1 unter Anwendung gewöhnlicher Fundamentaleinheiten sich bei Verzehnfachung des Reizes verdoppelt, dies nicht mehr stattfinden, wenn man natürliche Fundamentaleinheiten anwendet, weil die Empfindung 1 hier einem niederen Reizgrade, nicht dem 10 fachen, sondern 2,718.. .-fachen des Schwellenwertes zugehört, und mithin einer geringeren absoluten Größe der Empfindung entspricht. Diese wird sich verdoppeln, wenn der Reiz auf das 2,718... fache steigt.
Will man die Empfindungseinheit und Reizeinheit in demselben Punkte zusammentreffen lassen, so wird man die der vorigen nächst einfache Form der Maßformel erhalten, wenn man die Reizeinheit und die Empfindungseinheit zugleich bei einem fundamentalen Reizwerte nimmt, welcher gleich der Grundzahl der angewandten Logarithmen ist. Diese Form der Maßformel ist
Die Bedingung ferner, daß g und b zugleich 1 sind gibt durch Substitution von 1 sowohl für g als b in der Form der Maßformel (2) und Setzung von k = 1
Substituirt man endlich diese Werte k = 1 und - log b = + 1 in die allgemeine Form der Maßformel g = k (log b - log b), so erhält man die obige Form.
Die einfachste Form der Maßformel g = log b kann überall dienen und wird überall die einfachste Ableitung der Resultate gestatten, wo der Schwellenwert des Reizes konstant bleibt, indem man es dann immer in seiner Macht hat, die Fundamentaleinheiten anzuwenden, also die Einheit des Reizes konstant bei b, und die der Empfindung bei dem fundamentalen Reizwerte gleich der Grundzahl der angewandten Logarithmen zu nehmen. Wo jedoch Veränderungen der Reizbarkeit eintreten, oder die Möglichkeit derselben berücksichtigt werden soll, kann b nicht allgemein = 1 gesetzt werden; und wir werden uns daher in der Folge zwar häufig, aber nicht immer, der einfachsten Form der Maßformel bedienen.
Wie leicht zu erachten, führt die Abhängigkeit der Empfindung vom Reize von selbst die umgekehrte Abhängigkeit des Reizes von der Empfindung mit, nicht insofern der Reiz seinem Dasein nach in Abhängigkeit von der Empfindung stände, aber insofern die Größe des Reizes, welche nötig ist, eine gegebene Empfindung zu erwecken, in Abhängigkeit von der Größe der Empfindung steht. Dieses Abhängigkeitsverhältnis drückt sich mittelst Umkehrung der Maßformel aus durch
b = ag (11)
Die Formel g = k log ![]() führt nämlich zuvörderst zu log
führt nämlich zuvörderst zu log ![]() ,
diese nach Kap. 14 zu
,
diese nach Kap. 14 zu ![]() =
= ![]() und diese zu
und diese zu ![]() .
.
In Betreff der Bedeutung und Verwendung der Maßformel sind folgende Bemerkungen wichtig.
Sie ist eine Formel, welche nach ihrer Begründungsweise unmittelbar nur als maßgebend für die Abhängigkeit der Intensität oder Stärke der Empfindung von der Intensität oder Stärke des Reizes gelten kann, wenn ein Reiz an einem Punkte oder in gleichem Verhältnisse an allen Punkten, wo er besteht, ab- oder zunimmt. Wenn wir von Messung der Empfindung durch den Reiz mittelst der Maßformel sprechen, ist daher auch stets die Messung der Intensität der Empfindung nach der Intensität, nicht nach der Quantität des, über eine gegebene zeitliche oder räumliche Ausdehnung sich erstreckenden Reizes damit gemeint.
Soll die Empfindung einfach als Funktion des Reizes mittelst der Maßformel gemessen werden, so muß der Schwellenwert des Reizes b bekannt und ebenso wie k bei den verschiedenen Reizgraden konstant sein. Nun bleibt zwar k durch Reizeinwirkung ungeändert, wie ich unten besonders zeige, nicht aber b, indem sich durch Reizeinwirkung die Reizbarkeit ändert. Je mehr sie sich aber abstumpft, ein um so größerer Wert des Reizes gehört dazu, die Empfindung auf die Schwelle zu heben, um so mehr steigt also b. Inzwischen bebt dieser Umstand die Anwendbarkeit der Maßformel nicht auf, sondern erweitert sie vielmehr. Denn es zeigt sich hiermit, daß sie nicht bloß maßgebend ist für die Abhängigkeit der Empfindung vom Reize, sondern auch vom Grade der Empfindlichkeit, womit er aufgefaßt wird. Eben so, wie wir in die Formel ein variables b einführen und die davon abhängige Änderung von g verfolgen können, können wir ein variables b einführen und hiernach die Änderungen von g verfolgen.
Dies fordert natürlich dazu auf, das Gesetz der Änderungen von b durch Reizeinwirkung genauer zu studieren, um dann b als Funktion der Stärke und Dauer des Reizes in die Formel einführen zu können. Zu diesem Studium eines an sich wichtigen Verhältnisses aber bietet die Maßformel selbst den geeignetsten Anhalt dar. Wie es scheint, kommt b bei jedem nicht zu heftigen Reize mit verlängerter Dauer desselben zu einem Grenzwerte, oder, bei rascher periodischer Wiederkehr desselben, zu einem mittleren Werte, welche mit der Größe des Reizes und der Dauer der Periode in einer, jedoch noch nicht ermittelten, gesetzlichen Beziehung stehen; und es werden durch Substitution einesteils des Anfangswertes, anderenteils jenes Grenzwertes oder mittleren Wertes in die Maßformel Hauptfälle ihrer Anwendung gedeckt sein.
Wo der Schwellenwert b nicht bekannt ist, mithin ein absolutes Maß der Empfindung durch die Maßformel nicht stattfinden kann, läßt sich aber doch dieselbe zum Maße von Empfindungsunterschieden benutzen, indem, wenn man dieselbe für zwei verschiedene Empfindungen aufstellt, und den Unterschied der Ausdrücke nimmt, der Schwellenwert b aus diesem Unterschiede verschwindet, wie man schon hat bemerken können, und in einem späteren Kapitel noch weiter wird erörtert werden.
Stellt man in der Maßformel die Konstante b als Funktion der anderen Größen auf, so erhält man aus der Formel 11 die folgende
![]() (12)
(12)
wenn a die Grundzahl der angewandten Logarithmen
ist, wonach b dem Reize b proportional
ist, der eine gegebene Empfindung g mitführt.
Hiernach kann der reziproke Wert von b, d. i.![]() geradezu
als Maßstab der absoluten Empfindlichkeit oder der im Sinne von Th.
I. S. 51 verstandenen Reizbarkeit gelten, sofern auch diese nach früherer
Begriffsbestimmung dem Reize reziprok ist, der eine gegebene Empfindung
auslöst.
geradezu
als Maßstab der absoluten Empfindlichkeit oder der im Sinne von Th.
I. S. 51 verstandenen Reizbarkeit gelten, sofern auch diese nach früherer
Begriffsbestimmung dem Reize reziprok ist, der eine gegebene Empfindung
auslöst.
Hierbei ist vorausgesetzt, was in folgender Einschaltung bewiesen wird, daß k sich nicht mit b ändert.
Stellt man in der Maßformel k als Funktion der anderen Werte auf, so erhält man
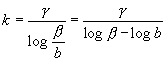 (13)
(13)
wonach k der Empfindung g
proportional ist, die durch ein gegebenes fundamentales Reizverhältnis ![]() hervorgeht. Nun ließe sich allgemein gesprochen als möglich
denken, daß, wenn der Schwellenwert des Reizes b sich vermöge
Abänderung der Reizbarkeit ändert, auch das fundamentale Reizverhältnis
hervorgeht. Nun ließe sich allgemein gesprochen als möglich
denken, daß, wenn der Schwellenwert des Reizes b sich vermöge
Abänderung der Reizbarkeit ändert, auch das fundamentale Reizverhältnis ![]() sich ändert, bei welchem eine gegebene Empfindungsgröße
g
entsteht. In diesem Falle würde voriger Formel zufolge der Wert k
sich mit dem Werte b ändern, davon abhängig sein, und
man also einen konstanten Wert von k in der Maßformel nur
so lange anwenden dürfen, als die absolute Empfindlichkeit oder Reizbarkeit,
von welcher b abhängt, dieselbe bleibt. Von der anderen Seite
aber ist allgemein gesprochen eben so denkbar, daß, wie auch der
Schwellenwert b sich ändere, doch die Empfindung dieselbe bleibt,
wenn nur das fundamentale Reizverhältnis
sich ändert, bei welchem eine gegebene Empfindungsgröße
g
entsteht. In diesem Falle würde voriger Formel zufolge der Wert k
sich mit dem Werte b ändern, davon abhängig sein, und
man also einen konstanten Wert von k in der Maßformel nur
so lange anwenden dürfen, als die absolute Empfindlichkeit oder Reizbarkeit,
von welcher b abhängt, dieselbe bleibt. Von der anderen Seite
aber ist allgemein gesprochen eben so denkbar, daß, wie auch der
Schwellenwert b sich ändere, doch die Empfindung dieselbe bleibt,
wenn nur das fundamentale Reizverhältnis ![]() dasselbe bleibt. In diesem Falle ist k unabhängig von der Reizbarkeit
und kann bei den verschiedensten Werten von b dasselbe k
in der Maßformel angewandt werden.
dasselbe bleibt. In diesem Falle ist k unabhängig von der Reizbarkeit
und kann bei den verschiedensten Werten von b dasselbe k
in der Maßformel angewandt werden.
Nur die Erfahrung kann diese wichtige Frage entscheiden, und sie entscheidet für die letzte Annahme. In dem Kapitel über das Parallelgesetz hat sich gezeigt, daß ein Unterschied zwischen zwei Reizen gleich deutlich erscheint, mögen sie mit ermüdeten Organen, wodurch der Schwellenwert b sich ändert, oder mit nicht ermüdeten aufgefaßt werden. Seien nun erstenfalls die zu einander gehörigen Werte der Konstanten b' und k', letztenfalls b und k, und beidesfalls die Reize, deren Unterschied aufzufassen ist, b und b1, so ist erstenfalls der Empfindungsunterschied
![]()
wovon sich die zweite Form ergibt, indem wir die Differenz der Logarithmen in den Logarithmus des Quotienten umsetzen. Zweitenfalls ist der Empfindungsunterschied
![]() .
.
Sollen nun beide Unterschiede gleich
sein, wie es die Erfahrung zeigt, so muß k' = k , d.
i. der Wert von k unabhängig vom Werte b sein 2)
Hiernach läßt sich aus der Maßformel folgender beachtenswerte Satz ableiten:
Wenn der Reizwert b, bei welchem
eine Empfindung auf die Schwelle tritt, sich in gegebenem Verhältnisse
vergrößert oder verkleinert, so vergrößert oder verkleinert
sich jeder Reizwert, durch welchen eine Empfindung gegebener Stärke
erzeugt werden soll, in demselben Verhältnisse. Wenn also z. B. Jemand,
der sich der Taubheit nähert, einen n-mal so starken Schall
braucht, um denselben überhaupt noch zuhören, als ein Anderer
mit gesunden Ohren, so wird er auch einen n-mal so starken Schall
brauchen, um ihn gleich stark als dieser zu hören, gleichviel, welche
Stärke man hierbei zu Grunde legen mag. Denn wir haben nach der Maßformel
g
= k log ![]() .
Soll nun bei n-fachem Werte von b der Wert von g
noch gleich groß ausfallen, als bei einfachem, so muß auch
das n-fache b angewandt werden.
.
Soll nun bei n-fachem Werte von b der Wert von g
noch gleich groß ausfallen, als bei einfachem, so muß auch
das n-fache b angewandt werden.
Wir haben kein direktes Mittel, die Stärke von Empfindungen bei verschiedenen Individuen zu vergleichen. Aber man sieht nicht ohne Interesse, daß wir durch Bestimmung des Schwellenwertes b bei verschiedenen Individuen ein indirektes Mittel erhalten, welches für die ganze Skale der Empfindungsstärken auf einmal ausreicht.
Übrigens zeigt die Form der Maßformel, daß es für die Größe der Empfindung auf dasselbe herauskommt, ob man b in einem gegebenen Verhältnisse verringert oder b in demselben Verhältnisse vergrößert denkt. Dies führt zu einer doppelten Repräsentation einer abgeänderten Reizbarkeit, und es kann unter Umständen sachgemäßer sein, sich der einen oder anderen zu bedienen. Man kann eine verminderte Reizbarkeit ebensowohl durch eine verminderte Reizeinwirkung b bei gleichem Schwellenwerte b repräsentieren, als durch einen erhöhten Schwellenwert b bei gleicher Reizeinwirkung b. Ersteres kann man als Abstumpfung der Reizeinwirkung oder des Reizes, Letzteres als Abstumpfung der Reizbarkeit bezeichnen. Bei Übersetzung des Reizes in die davon abhängige psychophysische Bewegung, welche aber erst in der inneren Psychophysik Platz zu greifen hat, ist nur die erste Repräsentation anwendbar, sofern eine verminderte Reizbarkeit voraussetzlich nur darin ruht, daß eine verminderte psychophysische Wirkung des Reizes stattfindet, die wir dann durch ein vermindertes b auszudrücken haben werden. Aber in der äußeren Psychophysik, auf deren Boden wir jetzt stehen, haben wir, um ohne Voraussetzung nur die faktischen Verhältnisse durch die Formel zu repräsentieren, den Reiz b in seiner wirklichen Größe in die Formel einzuführen, und die Variabilität seiner Wirkung nach Abänderung der Reizbarkeit durch eine Variation der Konstante b darzustellen, wobei wir also auch im Folgenden zunächst stehen bleiben.
Nennen wir B den Wert von b,
bei welchem die Einheit der Empfindung g angenommen
wird, so werden wir in den allgemeinen Ausdrücken, welche bisher für
b
und k gegeben wurden, den Wert von g
=
1 zu setzen haben, wenn wir zugleich b
=
B setzen. So erhalten wir diese Konstanten als Funktion des erfahrungsmäßigen
Wertes B, nämlich
(14)
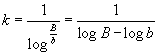 (15)
(15)Diese Werte für b und k lassen sich dann auch beliebig in die Maßformel substituieren. Bei Substitution des Wertes von b hat man
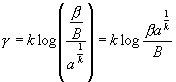
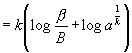
![]()
![]() (16)
(16)
Die Substitution von ![]() für log
für log![]() in dieser Herleitung, welche auf das schon (s.o.) gefundene Ergebnis zurückführt,
begründet sich dadurch, daß log
in dieser Herleitung, welche auf das schon (s.o.) gefundene Ergebnis zurückführt,
begründet sich dadurch, daß log ![]() =
= ![]() log
a,
und daß log a = 1, weil a die Grundzahl.
log
a,
und daß log a = 1, weil a die Grundzahl.
Bei Substitution des Wertes von k findet man leicht
 (17)
(17)Zu den bei der Anwendung der Maßformel zu berücksichtigenden Umständen gehört wesentlich das Vorhandensein innerer Empfindungsreize. Sofern solche vorhanden sind, ist ihre Größe der Größe der äußeren Reize hinzuzufügen, um den Wert von b zu erhalten, welcher in die Formel einzuführen ist. Es kann aber ihr Dasein und ihre Größe überhaupt nur aus dem Vorhandensein und der Stärke von Empfindungen bei Abwesenheit von äußeren Reizen erschlossen und nach Vergleichung mit deren Wirkung in einem Äquivalente berücksichtigt werden. So haben wir zu jedem äußeren Lichtreize eine kleine Größe hinzuzufügen und den so vermehrten Reiz in die Formel als b einzuführen, um das Resultat der Lichtempfindung vollständig zu erhalten, sofern sich nach mehrfacher früherer Erörterung schon ohne äußeren Reiz eine schwache Lichtempfindung im Dasein des Augenschwarz geltend macht, welche das Vorhandensein einer inneren Ursache der Lichtempfindung voraussetzt, die wir kurz als inneren Reiz bezeichnen. Läßt sich nun diese Zusatzgröße zum äußeren Reize nicht genau bestimmen, so muß doch ihr Dasein berücksichtigt werden, da sie bei schwachen äußeren Lichtreizen den wichtigsten Einfluß gewinnt, und müssen verhältnismäßig dagegen starke äußere Lichtreize angewandt werden, wo ihr Einfluß vernachlässigt werden soll.
Von der anderen Seite ist in Rücksicht zu ziehen, daß manche Reize abgesehen von der Abstumpfung der Reizbarkeit, die sie mitführen, einen ihre Einwirkung beschränkenden Mechanismus auslösen, dessen Wirkung mit der Stärke der Reize wächst. Mindestens gilt dies von dem Lichtreize, sofern sich die Pupille durch den verstärkten Lichtreiz verengert, und es wäre sehr möglich, daß beim Gehöre und vielleicht auch bei anderen Sinnen etwas Entsprechendes stattfände. Natürlich kann der Reiz nur mit Rücksicht auf diese Beschränkung in die Maßformel eingeführt werden, welcher man beliebig durch eine demgemäße Reduktion von b oder Steigerung von b genügen kann.
Jeder Reiz irradiiert in einem gewissen Umkreise und jeder klingt während einer gewissen Zeit nach; nachdem sein Eindruck einmal geschehen ist. Auch hieraus können zu berücksichtigende Zuwüchse zu dem direkt und momentan wirkenden Reize hervorgehen.
Noch in anderer Weise, nach Gesetzen des Kontrastes nämlich, wirken vorgängige und mitgehende Reize abändernd auf die Größe der Empfindung ein, die ein gegebener Reiz hervorruft. Soll mit Rücksicht hierauf die Maßformel einfache Anwendung finden, so müssen entweder alle Reize sich in demselben Verhältnisse ändern, oder es müssen alle Reize außer dem sich ändernden konstant gehalten werden; wenigstens ist es wahrscheinlich, daß unter diesen beiden Voraussetzungen die einfache Anwendung der Maßformel stattfinden kann. Das Weber’sche Gesetz nämlich bestätigt sich unter der ersten Voraussetzung beim Versuche mit den Wolkennuancen (Th. I. S. 140), unter der zweiten Voraussetzung bei Schätzung der Sterngrößen.
Endlich ist noch als eines, bei den Anwendungen der Maßformel zu berücksichtigenden Punktes der Aufmerksamkeit zu gedenken. Vorläufig fordern wir für eine vergleichbare Anwendung der Maßformel einen vergleichbaren Zustand der Aufmerksamkeit. Später wird sich zeigen, einmal, daß der verschiedene Grad der Aufmerksamkeit in gewissen Grenzen und in gewissem Sinne bei den Anwendungen der Maßformel auf Empfindungen nicht in Betracht kommt, zweitens, daß die Maßformel auf das Maß der Aufmerksamkeit selbst Anwendung finden kann. Hierzu jedoch müssen erst manche Erörterungen der inneren Psychophysik vorausgehen.
Man sieht nun wohl aus Vorstehendem, daß, so einfach die Maßformel ist, doch ihre Anwendung keine zu einfache Sache ist. Und es bietet sich bei diesen Schwierigkeiten ihrer Anwendung leicht die Frage dar, ob etwas und was überhaupt mit ihr gewonnen sei.
In dieser Hinsicht ist zu bemerken, daß das Hauptinteresse der Maßformel nicht sowohl darin liegt, daß sie gestattet, Empfindungen wirklich genau in Zahlwerten zu vergleichen, wozu nicht leicht ein wissenschaftlicher oder praktischer Anlaß sein dürfte, als daß:
1) mit der durch sie begründeten, unter günstigen Umständen zu verwirklichenden, prinzipiellen Möglichkeit des Maßes der Begriff desselben auf ein festes, klares, exaktes Fundament gebaut und hiermit der Psychophysik die mathematische Unterlage überhaupt gesichert ist; daß 2) in der funktionellen Verknüpfung der Werte g , b, b das Verhältnis von Reiz, Empfindung und Empfindlichkeit einen Ausdruck findet, welcher eine zugleich klare und scharfe Auffassung dieses Verhältnisses nach faktischer Beziehung begründet, und der Untersuchung darüber klare und sichere Angriffspunkte gewährt; daß 3) nach dieser funktionellen Beziehung sich auch ohne spezielles Maß doch im Allgemeinen voraussehen läßt, wie sich mit Abänderung dieser und jener Verhältnisse der Gang und Stand der Empfindungsphänomene ändern muß, wie es mit den Grenzfällen und Wendepunkten derselben steht; also auch da, wo kein speziales Maß möglich ist, doch allgemeine Folgerungen möglich werden.
Diese Vorteile bieten sich schon auf dem Gebiete der äußeren Psychophysik dar, und in solchen vielmehr, als in der eben so selten zu brauchenden als zu verwirklichenden Möglichkeit der Ausführung des Maßes ist die Wichtigkeit der Maßformel auf diesem Gebiete zu suchen.
Jedoch das Hauptinteresse der Maßformel ruht meines Erachtens überhaupt nicht in der äußeren, sondern in der inneren Psychophysik, sofern in der durch sie ausgedrückten Maßbeziehung zwischen Reiz und Empfindung zwar nicht der Eintritt in die innere Psychophysik, aber so zu sagen der Schlüssel zu ihrer Tür gegeben ist.
In der Tat, wenn schon die Maßformel sehr viel beitragen kann, uns in dem Gebiete der Beziehungen von Reiz und Empfindung zu orientieren, so wird doch nach allem Vorstehenden eine reine und strenge Anwendung derselben hier nie stattfinden können. Nur in gewissen, mehr oder weniger weiten, nie ganz sicher zu bestimmenden, Grenzen, mit mehr oder weniger Approximation, dürfen wir Proportionalität zwischen Reiz und dadurch ausgelöster psychophysischer Tätigkeit erwarten, und wo diese Proportionalität gestört ist oder aufhört, ist die Anwendbarkeit der Maßformel gestört oder aufgehoben. Die Hauptleistung der äußeren Psychophysik in Feststellung der Maßformel ruht daher meines Erachtens darin, sie trotz aller Störungen so weit auf ihrem Gebiete begründet zu haben, daß die Übersetzung in eine reine Anwendung auf dem Gebiete der inneren Psychophysik möglich und notwendig wird.
Inzwischen stehen wir doch für jetzt mit der Maßformel erst noch ganz in der äußeren Psychophysik, und haben ihre Leistungen und Beschränkungen zunächst auf diesem Boden in Betracht zu ziehen. Je vollständiger, getreuer, voraussetzungsloser aber dies geschieht, so besser werden wir dem Übertritte in die innere Psychophysik damit vorarbeiten.
Die Stärke der Reize im Gebiete des Lichtes und Schalles ist direkt durch ihre lebendige Kraft repräsentierbar, und von ihnen wie von anderen Reizen anzunehmen, daß sie nur als Reize wirken, sofern ihre lebendige Kraft eine lebendige Kraft psychophysischer Bewegung im Körper auslöst und mithin repräsentiert. Es hat hiernach ein Interesse, unsere Formeln als Funktion der lebendigen Kraft des Reizes oder der dadurch ausgelösten Bewegung aufzustellen. Zunächst zwar erscheint dies nur unter dem Gesichtspunkte einer mathematischen Spekulation; auch ist von vorn herein nicht zu entscheiden, ob Formeln, welche nach der Erfahrung zunächst nur für die lebendige Kraft ganzer Schwingungen aufgestellt werden konnten, auch übertragbar sind auf die lebendige Kraft der Einzelmomente von Schwingungen, und ob sich die Leistung einer ganzen Schwingung und sonst anderen Bewegungsformen für die Empfindung durch Summation dessen, was ihre einzelnen Momente nach diesen Formeln beitragen, richtig wiederfinden läßt, wodurch allein die Übertragung auf Momente gerechtfertigt und von Nutzen erscheinen könnte. Da sich inzwischen eine solche Rechtfertigung durch ein späteres Kapitel zu ergeben scheint, so schicken wir die darauf bezüglichen Elementarformeln voraus.
Denken wir uns ein Teilchen von der Masse m, das sich in einem gegebenen Zeitmomente mit der Geschwindigkeit v bewegt, und mithin die lebendige Kraft mv 2hat, vermöge deren es, sei es als Reiz auf ein Empfindungsorgan wirkt, oder selbst ein psychophysisch tätiges Element desselben darstellt, und hiermit so oder so einen Beitrag zur Totalempfindung gibt, die durch Summation der elementaren Wirkungen als hervorgehend anzusehen ist, wie dies künftig näher erläutert wird.
Sei b die Geschwindigkeit des Teilchens, bei welcher dessen Beitrag zur Gesamtempfindung erlischt; dann erhalten wir durch Substitution von mv2 für b und von mb² für b in die Maßformel
![]()
und in die Fundamentalformel
![]()
Die Gleichheit von ![]() mit
mit ![]() in
letzter Formel wird durch die Differenzialrechnung bewiesen, sofern d×v2
als Differenzial genommen = 2 vdv. Also haben wir kurz
in
letzter Formel wird durch die Differenzialrechnung bewiesen, sofern d×v2
als Differenzial genommen = 2 vdv. Also haben wir kurz
![]() ;
; ![]()
welche Werte noch mit dem Zeitelemente dt zu multiplizieren sein werden, um einerseits den Beitrag gdt zu erhalten, den ein Reiz, welcher zur Zeit t die Größe mv2 hat, zur Empfindung in dem Zeitelemente dt gibt, anderseits den Empfindungszuwachs dg dt, den die zur Zeit t stattfindende Empfindung erfährt, wenn der Reiz mv2 im Zeitelemente dt um d × mv2 wächst.
Aus vorigen Formeln fließen folgende beachtenswerte Folgerungen:
1) Die Maße der Teilchen geht in die Elementarformeln nicht ein.
2) Es ist gleichgültig, ob man die lebendige Kraft oder die einfache Geschwindigkeit in die Formeln einführt, indem sich letztenfalls bloß die Konstanten k und K verdoppeln.
3) Das Vorzeichen von v und mithin die Richtung der Geschwindigkeit ist einflußlos auf den Wert der Empfindung und des Empfindungsunterschiedes, indem stets gleiches Vorzeichen im Zähler und Nenner der Ausdrücke auftritt, denn auch b werden wir homolog dem v, wozu es gehört, vorauszusetzen haben.
Den ersten Punkt anlangend, so ist es unstreitig nicht ohne Interesse, und, wenn man will, dem Charakter eines geistigen Maßes angemessen, daß die körperliche Masse aus diesen Formeln ganz verschwindet. Die elementare geistige Intensität hängt danach nur von Bewegung, nicht von Masse ab. Indessen darf man das, was für Elemente gilt, nicht auf Systeme übertragen. Wenden wir die Formeln auf den Gesamtreiz an, so können sich die Impulse, welche verschiedene Teilchen desselben äußern, teils für denselben Punkt des empfindenden Organes summieren, wie denn zwei Glocken zusammen stärker als eine tönen, teils auf verschiedene verteilen, wie denn zwei Sterne zwei Lichtpunkte im Auge erscheinen lassen, und beidesfalls wird die Gesamtgröße der Empfindung mit der Zahl der reizenden Teilchen, hiermit der Gesamtmasse des Reizes, wachsen müssen. Wenden wir die Formeln auf das psychophysisch erregte Organ selbst an, so wird dasselbe von der Zahl der gereizten Teilchen gelten müssen. Auch wird unstreitig ein Teilchen von doppelter Masse mit gleicher Geschwindigkeit gleich einer Summe zweier Teilchen von einfacher Masse mit dieser Geschwindigkeit gelten müssen.
Die bisherigen Formeln sind nach der einfachsten und nächstliegenden Voraussetzung aufgestellt worden, daß die Abhängigkeit, welche nach der Erfahrung zwischen der Größe der Empfindung und der lebendigen Kraft einer ganzen Schwingung besteht, übersetzbar sei in eine Abhängigkeit zwischen dem Beitrage, den ein einzelnes Moment einer Schwingung in einem Zeitelemente zur ganzen Empfindung gibt, und der lebendigen Kraft, die in diesem Zeitelemente besteht, wobei sich gezeigt hat, daß es wesentlich auf dasselbe herauskommt, ob wir das Quadrat der Geschwindigkeit oder die einfache Geschwindigkeit für b in die Formeln einführen. Man kann nun aber bemerken, daß bei Licht und Schall, auf deren Verhältnissen wir hierbei allein fußen konnten, genau proportional mit der Geschwindigkeit der oszillierenden Teilchen die Änderungen der Geschwindigkeit wachsen, die im Laufe jeder Schwingung stattfinden; verdoppelt sich die Amplitude, so verdoppelt sich die Geschwindigkeit und verdoppelt sich die Änderung der Geschwindigkeit in jedem Momente zugleich. Und es ist hiernach eben so viel Grund, daran zu denken, daß für den Reiz b die Änderung der Geschwindigkeit als die Geschwindigkeit selbst in die Elementarformeln zu substituieren sei. Hierzwischen kann die Entscheidung nur danach kommen, welche von beiden Voraussetzungen der Aufgabe besser genügt, die erfahrungsmäßige Abhängigkeit der ganzen Empfindung von der ganzen Bewegung durch Summation elementarer Beiträge herzustellen; und es gibt einen verhältnismäßig einfachen Fall, der sich zur Untersuchung dieser Frage wohl eignet, auf den ich aber erst künftig eingehe.
Sollte nun nach solcher Untersuchung die Annahme wirklich vorzuziehen scheinen — und in der Tat wird es der Fall sein — daß in die Fundamentalformel und Maßformel für b statt der einfachen Geschwindigkeit die Änderung der Geschwindigkeit, oder was wir künftig kurz Geschwindigkeit zweiter Ordnung nennen werden, zu substituieren sei, um sie zur Konstruktion zusammengesetzter Empfindungsleistungen jeder Art tauglich zu machen, so würde dies übrigens in der Form der obigen Formeln nichts ändern, indem wir nur eben unter v statt einer Geschwindigkeit erster Ordnung eine solche zweiter Ordnung oder eine Geschwindigkeitsänderung zu verstehen haben würden, und die obigen drei Punkte würden eben so noch ihre Geltung behalten:
1) daß die Masse aus den Elementarformeln verschwindet;
2) daß es, abgesehen vom Werte der Konstanten k, K gleichgültig ist, ob man die Geschwindigkeiten zweiter Ordnung einfach oder im Quadrate verwendet;
3) daß der positive oder negative Wert derselben, d. h. ob sie als Beschleunigung oder Verzögerung wirken, keinen Einfluß auf das Empfindungsresultat hat.
Die genauere Untersuchung über die Frage selbst ist aber in der Tat erst später am Platze, da sich bis jetzt weder ein besonderes Bedürfnis noch auch ein Anhalt dargeboten hat, sie zu entscheiden.
Ich habe im Vorstehenden die Fundamentalformel und Maßformel nach den Hauptpunkten, die dabei in Betracht kommen, nur in so weit diskutiert, daß das Allgemeinste und der allgemeine Zusammenhang dieser Punkte ins Licht tritt; doch wird auf die einzelnen derselben in den folgenden Kapiteln noch mit spezielleren Erörterungen zurückzukommen, so wie die Anwendungen der Formeln zu verfolgen sein. Weiterhin komme ich auf eine Verallgemeinerung der Maßformel und des ganzen Maßprinzips, die ich hier vorweg kurz anzeige.
Die Maßformel gibt die Abhängigkeit der Empfindung vom Reize. Als das Allgemeinere derselben kann eine Formel, welche ich die Unterschiedsformel nenne, gelten, wodurch die Abhängigkeit eines Empfindungsunterschiedes vom Reizverhältnisse gegeben wird, indem die Maßformel als der besondere Fall der Unterschiedsformel angesehen werden kann, wo die eine beider Empfindungen, wozwischen der Unterschied besteht, Null wird. Die Formeln für Empfindungsunterschiede lassen sich weiter zu solchen für Unterschiede zwischen Empfindungsunterschieden oder Unterschieden höherer Ordnung verallgemeinern. Zwischen Empfindungsunterschieden ist selbst ein später durch Tatsachen zu erläuternder Unterschied zu machen, je nachdem sie in der Empfindung aufgehen oder besonders aufgefaßt werden sollen, und für letztere die Einführung der Verhältnisschwelle in die Unterschiedsformel nötig, wodurch die Unterschiedsmaßformel entsteht. Endlich läßt sich das ganze Maßprinzip vom Weber’schen Gesetze unabhängig darstellen.