§ 152. Man kann fragen, ob
die Mitteltemperaturen der aufeinanderfolgenden Jahre nach reinem Zufallsgesetze
variieren oder eine gewisse Abhängigkeit in ihrer Aufeinanderfolge
von einander zeigen; eine Frage, die auf viele analoge Fälle übertragen
werden kann. Nun können die Abhängigkeitsverhältnisse verschieden,
und die Untersuchungen darauf demgemäß verschieden zu führen
sein. Eine der einfachsten Fragen und Untersuchungswege aber knüpft
sich an folgende Bemerkung.
Ich nehme eine Liste gezogener Lotterienummern. Eine solche beginnt beispielsweise mit:
26 826 _
21 460 +
31 094 _
22 120 _
16 226 (+)
Ich bezeichne, wie beistehend, jede Abnahme von einer zur folgenden Nummer mit , jede Zunahme mit + und erhalte so ohne Rückgreifen auf die erste Nummer folgende Reihe: + und hiervon ohne Rückgreifen auf das erste Vorzeichen zwei Zeichenwechsel und eine Folge gleicher Zeichen; oder wenn ich sowohl mit Zahl als Zeichen zurückgreife: + + und hierin vier Wechsel und eine Folge; allgemein, wenn ich die Zahl der Nummern m und die Zahl der Wechsel und Folgen z nenne, erstenfalls z = m 2 , letzterenfalls z = m . Ersteres heiße Methode a , letzteres Methode b .
Mag ich nun die Methode a oder
b
anwenden,
so finde ich bei großem m die Zahl der Zeichenwechsel so approximativ
gleich dem Doppelten der Zahl der Zeichenfolgen, daß ich die
W. der einen zur W. der anderen wie 2
: 1 annehmen kann1).
Dies das Gesetz des reinen Zufalls.
1) [Theoretisch leitet man dieses Verhältnis aus der Bemerkung ab, daß drei Werte a, b, c, die frei von Successionsabhängigkeit sind, mit der nämlichen Wahrscheinlichkeit in jeder der sechs Successionen:
a , b , c ,
c , b , a ,
b , a , c ,
c , a , b ,
a , c , b ,
auftreten können, so daß, wenn z. B. a <b
< c, die beiden ersten Successionen je eine Zeichenfolge,
die vier letzten je einen Zeichenwechsel ergeben, und mithin die W. einer
Zeichenfolge gleich 1/3
die W. eines Zei-chenwechsels gleich 2/3zu
setzen ist.]
Sollte aber eine Abhängigkeit der aufeinander folgenden Zahlen der Art stattfinden, daß sie in kontinuo durch ein gewisses Intervall stiegen und wieder sänken, so würde die Zahl der Zeichenfolgen sich über das vorige Verhältnis hinaus vergrößern. Ja, wenn die Abhängigkeit immer in derselben Richtung fortginge, so würde man nach Methode a lauter Zeichenfolgen, nach Methode b m 2 Folgen, 2 Wechsel erhalten.
Bleiben wir bei Methode a stehen und nennen die Zahl der Wechsel w , die der Folgen f ,so wird die volle Unabhängigkeit durch f = 1/3z , die volle Abhängigkeit durch f = z und die partielle Abhängigkeit durch Werte von f zwischen diesen charakterisiert, und man wird ein Maß der partiellen Abhängigkeit bei gegebenem f und z in dem Verhältnisse finden können, in welchem der Überschuß von f über das Maß der vollen Unabhängigkeit zum Totalüberschuß der vollen Abhängigkeit über die volle Unabhängigkeit steht, d. i. wenn wir dieses Maß mit Abh. bezeichnen:
Abh. = ![]() . (1)
. (1)
Inzwischen ist f wegen des endlichen m unsicher, und von dieser Unsicherheit ist Abh. mit beteiligt. Die Bestimmung dieser Unsicherheit ist in den Wert von Abh. als wahrscheinlicher Fehler mit aufzunehmen.
[Man leistet diese Bestimmung durch Berechnung der wahrscheinlichen Grenzen, die sich aus der Umkehrung des sog. BERNOULLI-schen Theorems für die W. einer Zeichenfolge auf Grund der beobachteten Werte von f und z ergeben. Setzt man nämlich die unbekannte W. für das Auftreten einer Zeichenfolge gleich x , die W. eines Zeichenwechsels gleich 1- x , so besteht dem angeführten Satze der Wahrscheinlichkeitsrechnung2) zufolge die W.:
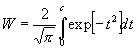 (2)
(2)
dafür, daß der Wert von x zwischen den Grenzen:
![]() und
und ![]() (2a)
(2a)
liege. Da nun für W = ½ der Wert von c = 0,476 94 wird, so sind die wahrscheinlichen Grenzen von x gleich:
![]() . (3)
. (3)
Dem entsprechend sind die wahrscheinlichen Grenzen von Abh. gleich:
![]() . (4)
. (4)
Es ist somit 1 gegen 1 zu wetten, daß das wie oben
definierte Maß der Abhängigkeit nicht kleiner als die untere
und nicht größer als die obere der beiden angegebenen Grenzen
sei.]
2) [Vergl. MEYER's Vorlesungen über Wahrscheinlichkeitsrechnung
Kap.VII.]
[Dasselbe kann auch negative Werte annehmen und so eine Abhängigkeit anzeigen, die sich durch vorwiegenden im extremen Falle durch ständigen Wechsel der Zeichen kund gibt. Hierzu ist erforderlich, daß die Anzahl f der Zeichenfolgen unter den Wert 1/3z sinke und im Grenzfalle gleich 0 werde.]
§ 153. [Die Anwendung des Abhängigkeitsmaßes (4) zur Prüfung der Sukzessionsabhängigkeit meteorologischer Monats- und Tageswerte führt zu folgenden Resultaten.]
[DOVE stellt in einer seiner Abhandlungen3) für eine Reihe von Orten die "Abweichungen der einzelnen Monate vom vieljährigen mittleren Werte derselben" zusammen. Für Berlin umfaßt diese Zusammenstellung den Zeitraum von 1719 bis 1849 mit dem Ausfalle von bloß 3 bis 7 Jahren für die einzelnen Monate. Hieraus ergeben sich für alle Monate zusammen genommen nach Methode a 1421 Sukzessionen von Zeichen, und zwar 913 Zeichenwechsel und 508 Zeichenfolgen. Die W. x einer Zeichenfolge hat somit die wahrscheinlichen Grenzen:
Abh. = 0,036 ± 0,013
erhält.]
3) [Bericht über die in den Jahren 1848 und 1849 auf
den Stationen des meteorologischen Instituts angestellten Beobachtungen.
Berlin 1851. S. XX flgd.]
[Im Niederländischen Jahrbuche für Meteorologie4) findet man Tabellen der täglichen Thermometer- und Barometerabweichungen von dem aus langjähriger Beobachtung gefundenen täglichen Normalstande, für die einzelnen Monate des Jahres. Die Beobachtungsorte sind die verschiedenen meteorologischen Stationen des Landes; die Beobachtungszeiten sind bestimmte Stunden des Tages, auf welche sich sowohl der Normalstand als auch die Abweichungswerte beziehen. Hierdurch wird dem gesetzmäßigen Steigen oder Fallen des Thermometers und Barometers innerhalb eines Monats Rechnung getragen, so daß die Sukzessionsabhängigkeit nicht davon beeinflußt wird. Ich wählte die für Utrecht im Monat Januar während des 10-jährigen Zeitraumes von 1884 bis 1893, mittags 2 Uhr, angegebenen Werte. Dieselben ergaben nach Methode a 298 Sukzessionen von Zeichen. Darunter waren für die Thermometerabweichungen 129 Zeichenfolgen und 169 Zeichenwechsel, für die Barometerabweichungen 153 Zeichenfolgen und 145 Zeichenwechsel. Sonach findet man für erstere die wahrscheinlichen Grenzen der W. einer Zeichenfolge gleich:
0,433 ± 0,019
und:
Abh. = 0,149 ± 0,029 ;
für letztere dagegen als wahrscheinliche Grenzen der W. einer Zeichenfolge:
Abh. = 0,270 ± 0,029 .
4) [Meteorologisch Jaarboek, uitgegeven door het Kon. Nederlandsch
Meteorologisch Instituut. "Thermoen Barometer-afwijkingen".]
[Die täglichen Regenhöhen sind dagegen nach einer Bemerkung in § 21 frei von wesentlicher Sukzessionsabhängigkeit. In der Tat ergeben die im XXI. Kapitel als Beispiel für die logarithmische Behandlung gewählten Regenhöhen des Monats Januar für Genf von 18451892 unter 475 Sukzessionen von Zeichen 165 Folgen gleicher Zeichen. Dabei sind sämtliche 477 Werte ihrer zeitlichen Aufeinanderfolge nach in eine Reihe vereinigt, und die Sukzessionen gleicher Werte abwechselnd den Zunahmen und den Abnahmen beigerechnet worden. Somit findet sich:
§ 154. [Ein anderer Weg zur Untersuchung der Sukzessionsabhängigkeit wurde in § 20 zugleich mit dem bisher erörterten bezeichnet. Er gründet sich auf die Bemerkung, daß bei voller Unabhängigkeit und ohne Störung durch unausgeglichene Zufälligkeiten die Anzahl der Folgen von je zwei oberhalb oder je zwei unterhalb der Wertmitte C gelegenen Maßwerten gleich sei der Anzahl der Wechsel zwischen je zwei oberhalb und unterhalb C gelegenen Werten. Werden nämlich die Werte oberhalb C durch + , die Werte unterhalb C durch - bezeichnet, so ist die W. eines positiven Wertes ebenso groß wie die W. eines negativen; es ist daher auch bei voller Unabhängigkeit jede der vier möglichen Sukzessionen: + +; - - ; + - ; - + gleich wahrscheinlich. Die beiden ersten ergeben aber je eine Zeichenfolge, die beiden letzten je einen Zeichenwechsel, so daß sowohl für eine Zeichenfolge als auch für einen Zeichenwechsel die W. ½ besteht. Findet man nun für eine in dieser Weise behandelte Reihe von Werten f Zeichenfolgen und w Zeichenwechsel bei einer hinreichend großen Anzahl von z = f + w Sukzessionen von Zeichen, so können ebenso wie oben die wahrscheinlichen Grenzen für die unbekannte W. x einer Zeichenfolge aus der Umkehrung des BERNOULLI'schen Theorems gleich:
![]()
gefunden werden. Hier wird sich der Wert f : z bei stattfindender partieller Sukzessionsabhängigkeit, die sich als Häufung der Folgen im Vergleiche zu den Wechseln zu erkennen gibt, zwischen dem Werte ½ , der für volle Unabhängigkeit gilt, und dem Werte 1, der für f = z volle Abhängigkeit anzeigt, halten. Man kann daher wiederum in dem Verhältnisse des Überschusses der partiellen Abhängigkeit über die volle Unabhängigkeit, d. i. des berechneten x über ½ , zu dem Totalüberschusse der vollen Abhängigkeit über die volle Unabhängigkeit, d. i. von 1 über ½ , ein Maß der Abhängigkeit gewinnen und
Abh.=![]() (6)
(6)
setzen. Auch dieses Maß der Abhängigkeit behält für negative Werte seine Bedeutung, indem es alsdann das Überwiegen der W. eines Zeichenwechsels über die W. einer Zeichenfolge anzeigt.]
[Als Beispiel für diese Abhängigkeitsbestimmung diene einesteils die Reihe der Monatsabweichungen für Berlin, anderenteils die Reihe der Rekrutenmaße, deren Sukzessionsabhängigkeiten nach Formel (4) bereits berechnet wurden, so daß zugleich ein Vergleich zwischen beiden Weisen der Bestimmung möglich wird.]
[Bezüglich der Monatsabweichungen ist zunächst für jeden Monat die Wertmitte C zu bestimmen. Dieselbe fällt für einige Monate unterhalb, für die Mehrzahl der Monate oberhalb des jeweiligen vieljährigen Mittels. Es kann indessen was die Anwendung dieser Methode sehr erleichtert sehr wohl der Mittelwert selbst als Wertmitte angenommen werden, so daß die positiven und negativen Abweichungswerte zugleich als + Werte und - Werte im Sinne unserer Methode gelten dürfen. Denn die 12 Monate ergeben, zusammengenommen, nach Bestimmung der Zentralwerte 768 Zeichenfolgen und 665 Zeichenwechsel; bei direkter Bezugnahme auf die Mittelwerte dagegen finden sich 769 Zeichenfolgen und 664 Zeichenwechsel, was keinen wesentlichen Unterschied für das Abhängigkeitsmaß mit sich führt. Aus ersteren Bestimmungen resultieren als wahrscheinliche Grenzen für die W. einer Zeichenfolge die Werte:
[Der Zentralwert C der 360 Rekrutenmaße findet sich gleich 71,75. Hiernach ergehen sich unter 359 Sukzessionen von Zeichen 165 Zeichenfolgen und 194 Zeichenwechsel. Die wahrscheinlichen Grenzen für die W. einer Reihenfolge sind daher:
§ 155. [Das Abhängigkeitsmaß (6) kann auch der Bestimmung der wechselweisen Abhängigkeit von je zwei Dimensionen eines mehrdimensionalen K.-G. oder von Dimensionen verschiedener, aber zeitlich zusammengehöriger K.-G. dienstbar gemacht werden. Zu diesem Zwecke bezeichne man das Wachsen von jeder der beiden verglichenen Dimensionen durch +, das Abnehmen durch - , so daß eine Reihe von m Paaren zusammengehöriger Werte durch m 1 Zeichenpaare ++, - - , + - , - + charakterisiert wird. Unter letzteren werden sich bei voller Unabhängigkeit der beiden Dimensionen von einander und ohne Hinzutreten unausgeglichener Zufälligkeiten ebensoviele Zeichenfolgen als Zeichenwechsel befinden, da die W. für jede der vier Arten von Zeichenpaaren gleich groß anzunehmen ist. Es ist daher, wenn unter z Beobachtungen f Folgen und w Wechsel auftreten, die W. einer Zeichenfolge nach Formel (3) zu berechnen und das Abhängigkeitsmaß nach Formel (6) zu bestimmen.]
So besteht beispielsweise zwischen der Größe des Horizontalumfanges und des vertikalen Scheitelbogens der 500 europäischen Männerschädel, die im vorigen Kapitel der Behandlung von Verhältnissen zwischen Dimensionen als Beispiel dienten, eine Abhängigkeit, die sich nach der angegebenen Methode wie folgt bestimmen läßt. Die 500 Schädelmasse sind in der Urliste in 34 Gruppen von 6 bis 30 Schädel zusammengefaßt (die beiden ersten enthalten 20 Breisgauer und 15 Schwaben; die beiden letzten 6 Serben und 22 Großrussen); in jeder Gruppe aber sind die Maße nach wachsendem Horizontalumfange geordnet. Ich zählte nun für jede Gruppe die Anzahl der Zeichenfolgen und Zeichenwechsel ab, die sich für den Gang der beiden verglichenen Werte ergeben, wobei die Fälle, in denen ein Stillstand in der Veränderung einer der beiden Größen eintrat, zur Hälfte den Folgen und zur Hälfte den Wechseln beigezählt wurden. Hiernach fanden sich 273 Zeichenfolgen und 193 Zeichenwechsel unter 466 Zeichenpaaren, so daß sich:
[Ein zweites Beispiel entnehme ich den von Prof. WELCKER in der Abhandlung5): "die Kapazität und die drei Hauptdurchmesser der Schädelkapsel" mitgeteilten Maßen des Innenraumes I und der Länge L , Breite B und Höhe H von 101 Schädeln verschiedener Völkerschaften, um insbesondere die Abhängigkeit des WELCKER-schen "Schädelmodulus" L+B+H und des Produktes L× B × H vom zugehörigen Innenraume zu berechnen. Werden die einzelnen, nach zunehmendem Innenraume geordneten Schädelgruppen, deren Anzahl 13 ist, hier ebenso behandelt wie bezüglich der Gruppen der Horizontal- oder Vertikalmaße angegeben wurde, so resultieren sowohl für L+B+H und I als auch für L . B . H und I 59,5 Zeichenfolgen gegenüber 26,5 Zeichenwechsel unter 86 Zeichenpaaren. Es ist somit sowohl für die Abhängigkeit der Summe als des Produktes der drei Hauptdurchmesser vom Innenraume: