[Hieraus erwächst die Aufgabe, in Ergänzung des bereits im V. Kapitel (§ 35 und 36) Gesagten auf die logarithmische Behandlung überhaupt näher einzugehen. Dort wurden die allgemeinen Gesichtspunkte entwickelt, die es geboten erscheinen lassen, das Verteilungsgesetz der K.-G. prinzipiell vielmehr auf Verhältnisabweichungen als auf arithmetische Abweichungen zu beziehen, woraus unmittelbar die Folgerung sich ergab, daß dem G. G. statt der arithmetischen Q = a H die Logarithmen der Verhältnisabweichungen y= a : H , nämlich log y = log a - log H , zu Grunde zu legen seien. Auch wurde dort die Anwendung der logarithmischen Behandlung der Hauptsache nach schon mitgeteilt und die Bezeichnungsweise festgesetzt. Demgemäß ist allgemein:
zu setzen und insbesondere der dichteste Wert der a durch D, ihr arithmetisches Mittel durch G und ihr Zentralwert durch C zu bezeichnen, während die oberen und unteren Abweichungszahlen und mittleren Abweichungen bez. D in gleicher Weise wie bez. D durch m' ,m, und e' , e,anzugeben sind, so daß:
![]() ;
; ![]() ; wo
l¢
= a¢-
D
;
l
, = D a,.
(2)
; wo
l¢
= a¢-
D
;
l
, = D a,.
(2)
Will man ferner von den logarithmischen Werten zu den Zahlwerten übergehen, die ihnen nach den Logarithmentafeln zugehören, so ist
D = log T ; C = log C ; G = log G (3)
vorauszusetzen. Es bezeichnet alsdann T den dichtesten Verhältniswert der a , der von dem arithmetisch dichtesten Werte D verschieden ist; C stimmt mit dem arithmetischen Zentralwerte überein; und G stellt das geometrische Mittel der a dar. Mit dem Hinweis auf diese Festsetzungen und Entwicklungen des angegebenen Kapitels verbindet sich aber die Verpflichtung, was dort nur in Aussicht gestellt wurde, hier durchzuführen. Es müssen darum einesteils die empirischen Belege dafür erbracht werden, daß in der Tat der Vorteil der logarithmischen Behandlung für K.-G. mit starker verhältnismäßiger Schwankung entschieden hervortritt. Anderenteils gilt es, die für die logarithmischen Abweichungen der a und ihre Hauptwerte D ,C ,G auf Grund des zweispaltigen G. G. unmittelbar geltenden Bestimmungen auf die Verhältnisabweichungen der a und ihre Hauptwerte T , C , G zu übertragen und durch Ableitung der theoretisch gültigen Beziehung zwischen T und D einen Zusammenhang zwischen der logarithmischen und arithmetischen Behandlung herzustellen.]
[Hierbei ist das logarithmische Verteilungsgesetz selbst als ein bei starker Schwankung hinreichend sich bewährendes Erfahrungsgesetz anzusehen, das bei schwacher Schwankung in das gewöhnliche arithmetische Gesetz übergeht. Jenes bedarf daher sowenig wie dieses vom empirischen Standpunkte aus einer weiteren Begründung. Nachdem aber im Zusatze zum XIX. Kapitel eine Hypothese betreffs der Entstehungsweise der K.-G-, aufgestellt worden, aus der das zweiseitige G. G, für arithmetische Abweichungen approximativ sich ergab, erscheint es geboten, jene Hypothese so zu modifizieren, daß aus ihr auch für logarithmische Abweichungen das Verteilungsgesetz in entsprechender Weise folgt. Dies soll im Zusatz zu diesem Kapitel geschehen.]
§ 144. [Um den Vorzug, den die logarithmische Behandlung gegenüber der arithmetischen bei starker Schwankung besitzt, vor Augen zu stellen, entnehme ich jedem der oben genannten K.-G., den Dimensionen der Galleriegemälde und den täglichen Regenhöhen, ein Beispiel und teile die Resultate für beide Behandlungsweisen mit.]
[Aus den Katalogen der älteren
Pinakothek zu München und der Gemäldesammlung zu Darmstadt ergaben
sich die Maße von 253 Genrebildern, deren Höhendimensionen in
eine primäre Verteilungstafel gebracht wurden. Als Maßeinheit
wurde das Zentimeter gewählt. Das kleinste Maß fand sich gleich
13, das größte gleich 265, das arithmetische Mittel A1gleich
54,4 und der Zentralwert C1gleich
44,2 cm. Hieraus wurde eine reduzierte Tafel gewonnen, in welcher die Maße
für je 10 cm zusammengefaßt wurden. Dieselbe führte bei
arithmetischer Behandlung nach dem zweiseitigenG. G. zu folgenden Ergebnissen:
|
|
|
||
|
|
|
||
| | | 1 | |
| 15 | 13 | 15 | |
| 25 | 41 | 38 | |
| 35 | 54 | 39 1) | |
| 45 | 43 | 36 | |
| 55 | 22 | 31 | |
| 65 | 20,5 | 26 | |
| 75 | 15 | 21 | |
| 85 | 10 | 16 | |
| 95 | 8,5 | 11 | |
| 105 | 5 | 8 | |
| 115 | 3 | 5 | |
| 125 | 6 | 3 | |
| 135 | 3 | 2 | |
| 145 | 5 | 1 | |
| 155 | 0 | | |
| 165 | 1 | | |
| 195 | 1 | | |
| 235 | 1 | | |
| 265 | 1 | | |
C2 = 44,3
Di = 35,4
Dp = 24,9
m' = 220
1) [Hier fällt das Maximum der theoretischen Werte nicht
auf das Intervall 20 - 30, welches den dichtesten Wert Dp
einschließt. Dies wird jedoch nur durch die obige intervallweise
Zusammenfassung der z bedingt. In der Tat findet man bei anderer
Zusammenfassung beispielsweise:
|
|
|
|
|
|
|
|
|
|
|
|
so daß ein geringer Überschuß dem Intervall 24 - 28
mit dem dichtesten Werte 24,9 zukommt.]
Ersetzt man aber in der primären Tafel die a -Werte durch die logarithmischen Werte a = log a , die nunmehr zwischen den Grenzen a= 1 ,11 und a= 2,42 variieren, und wählt man ein reduziertes Intervall von der Größe 0,08, so erhält man, wenn diese Tabelle der aganz ebenso behandelt wird wie die vorige Tabelle der a , folgende Resultate:
II. Höhendimension der Genrebilder in logarithmischer
Behandlung.
i = 0,08 ; m = 253 .
|
|
|
|
|
|
|
|
| 1,04 | |
0,5
|
| 1,12 | 4 |
1,5
|
| 1,20 | 5 |
4
|
| 1,28 | 5 |
10
|
| 1,36 | 19 |
18
|
| 1,44 | 22 |
27
|
| 1,52 | 38 |
32
|
| 1,60 | 32 |
32
|
| 1,68 | 31 |
30
|
| 1,76 | 26 |
26
|
| 1,84 | 18 |
22
|
| 1,92 | 19 |
17
|
| 2,00 | 13 |
12
|
| 2,08 | 9 |
8,5
|
| 2,16 | 8 |
5,5
|
| 2,24 | 1 |
3
|
| 2,32 | 1 |
2
|
| 2,40 | 2 |
1
|
| 2,48 | |
1
|
G = 1,669
C = 1,644
Di = 1,538
Dp = 1,549
G = 46,7
C = 44,1
Ti = 34,5
Tp = 35,4
m' = 165
m,= 88
e' = 0,256
e,= 0,136
![]()
![]()
Vergleicht man nun beide Tabellen, so tritt der Vorteil der logarithmischen Behandlung entschieden zu Tage. Denn in der arithmetischen Tafel ist die Summe der absoluten Differenzen zwischen empirischen und theoretischen Werten gleich 74; in der logarithmischen Tafel dagegen nur gleich 37, also genau halb so groß. Es weichen ferner der empirische und der theoreti-sche dichteste Wert, Diund Dp, um 10,5 Einheiten von einander ab; während die mit jenen vergleichbaren Werte Tiund Tpnur um 0,9 sich unterscheiden. Auch ist zu erwähnen, daß der arithmetisch bestimmte Quotient
![]()
den Wert 0,64 , der logarithmisch bestimmte Quotient
![]()
den Wert 0,792 darstellt, so daß jener ganz außerhalb der theoretischen Grenzen von p , d. i. 0,785 und 0,845, fällt, während dieser dem durch die p -Gesetze geforderten Werte ¼p = 0,785 innerhalb jener Grenzen sehr nahe kommt. All dies zeigt, daß in der Tat die arithmetische Behandlung hier versagt, die logarithmische dagegen sich bewährt. Dabei ist zu beachten, daß trotz des geringen m der empirischen Tafel die hervorgehobenen Beziehungen für die Dimensionen der Genrebilder als typisch zu gelten haben.]
[Als Beispiel für die täglichen Regenhöhen sollen die in Genf während der Jahre 1845 1892 im Monat Januar gefallenen Regenmengen (geschmolzener Schnee oder Regen) dienen, die in den meteorologischen Tabellen der Bibliothèque Universelle de Genève (Archives des Sciences Phys. et Nat.) unter der Rubrik "Eau tombée dans les 24 heures" verzeichnet sind. Die Gesamtzahl der Regentage während des bezeichneten Zeitraumes von 48 Jahren beträgt 477; für jeden derselben sind die Regenhöhen bis auf Zehntelmillimeter angegeben. 16 Regentage sind mit 0,0 mm verzeichnet; die größte Regenhöhe ist gleich 40,0; das arithmetische Mittel A1gleich 4,45; der Zentralwert C1gleich 2,24 mm. Aus der primären Verteilungstafel wurde eine reduzierte Tafel mit dem Intervall i = 1 mm hergestellt, die bei arithmetischer Behandlung folgende Werte ergab:
III. Die Regenhöhen des Monats Januar für
Genf in arithmetischer Behandlung.
m = 477 ; i = 1 ; A1
= 4,45 ; E = 1mm.
|
|
|
|
| emp. | theor. | |
| 0,5 | 133 | 67 |
| 1,5 | 88 | 63 |
| 2,5 | 43,5 | 61 |
| 3,5 | 28 | 56 |
| 4,5 | 27 | 49 |
| 5,5 | 28 | 42 |
| 6,5 | 27,5 | 35 |
| 7,5 | 14,5 | 28 |
| 8,5 | 16 | 22 |
| 9,5 | 11,5 | 16 |
| 10,5 | 12 | 12 |
| 11,5 | 10 | 8 |
| 12,5 | 6,5 | 6 |
| 13,5 | 5,5 | 4 |
| 14,5 | 3 | 2 |
| 15,5 | 3 | 2 |
| 16,5 | 2 | 1 |
| 17,5 | 5 | 1 |
| 18,5 | 1 | |
| 19,5 | 3 | |
| 20,5 | 0 | |
| 21,5 | 3 | |
| 22,5 | 0 | |
| 23,5 | 2 | |
| 28,5 | 1 | |
| 30,5 | 1 | |
| 32,5 | 1 | |
| 40,0 | 1 | |
IV. Die Regenhöhen des Monats Januar für
Genf in logarithmischer Behandlung.
m = 477 ; i = 0,2 .
|
|
|
|
| empir. | theor. | |
| | | 5 |
| - 1,4 | 8 | 4 |
| - 1,2 | 8 | 6 |
| - 1,0 | 9 | 9 |
| - 0,8 | 9 | 14 |
| - 0,6 | 28 | 19 |
| - 0,4 | 14 | 26 |
| - 0,2 | 34 | 34 |
| 0,0 | 45 | 42 |
| + 0,2 | 66 | 50 |
| + 0,4 | 47 | 56 |
| + 0,6 | 53 | 60 |
| + 0,8 | 67 | 63 |
| + 1,0 | 53 | 52 |
| + 1,2 | 27 | 27 |
| + 1,4 | 7 | 8 |
| + 1,6 | 2 | 2 |
C = 0,374 C = 2,37
Di= 0,800 Ti= 6,31
Dp = 0,843 Tp = 6,97
Es zeigen zwar hier die unterhalb des dichtesten Wertes liegenden z bei - 0,4 und + 0,2 starke Unregelmäßigkeiten, die bei Änderung der Reduktionslage nicht verschwinden, vielmehr durch den Gang der z in der primären Tabelle und deren Zusammenfassung in die logarithmischen Intervalle begründet sind; trotzdem ist aber die Übereinstimmung zwischen Theorie und Erfahrung so gut, daß die Differenzen zwischen den theoretischen Werten und den empirischen als eine Ausgleichung der Zufälligkeiten, die letzteren anhaften, sich darstellen. Es bewährt sich somit das logarithmische Verteilungsgesetz auch an den Regenhöhen durchaus befriedigend.]
§ 145. [Auf Grund des im Vorstehenden durchgeführten Vergleiches zwischen Theorie und Erfahrung erweist sich das logarithmische Verteilungsgesetz für K.-G. mit starker verhältnismäßiger Schwankung als zutreffend. Da nun dasselbe nach den Erörterungen des V. Kapitels bei schwacher verhältnismäßiger Schwankung der Einzelwerte um die Hauptwerte mit der arithmetischen Verallgemeinerung des G. G. merklich übereinstimmt, so ist es wie am Schlusse des angegebenen Kap. schon hervorgehoben wurde überhaupt als das streng gültige Verteilungsgesetz der K.-G. in Anspruch zu nehmen. Somit bestimmt sich die Wahrscheinlichkeit W¢ oder W,, daß eine logarithmische Abweichung vom dichtesten Werte D zwischen die unendlich nahen Grenzen l ' und l ' + dl¢ oder l, und l,+ dl, falle für jeden K.-G. durch:
![]() ;
;
![]() ; (4)
; (4)
und es findet sich die Anzahl der Abweichungen zwischen den angegebenen Grenzen gleich:
[Für die Hauptwerte G ,Cund D der logarithmischen Abweichungen gelten daher die nämlichen Gesetze, die im XIX. Kapitel für die arithmetischen Hauptwerte A , C und D abgeleitet wurden. Ersetzt man aber G ,C und D der Reihe nach durch log G , log C und log T ,so erhält man unmittelbar die für die Hauptwerte G , C und T der Verhältnisabweichungen gültigen Gesetze.]
[Es ergeben sich so insbesondere folgende Bestimmungen:
e' = log G' - log T ; e,= log T - log G,,
so ist auf Grund des Proportionalgesetzes:
e' - e, = log G - log T ; (6)
G' × G,= G × T .
[Den Zusammenhang zwischen den arithmetischen Hauptwerten und denjenigen der Verhältnisabweichungen schließlich stellen folgende Sätze her.]
Zum logarithmischen Mittelwerte G
=
ålog
a:
m als Logarithmus gefaßt gehört der mit G
zu bezeichnende,
sogenannte geometrische Mittelwert oder Verhältniswert, welcher stets
rücksichtslos auf ein bestimmtes Verteilungsgesetz etwas kleiner als
der arithmetische Mittelwert
A = åa:
m ist und (nach einem Beweise von SCHEIBNER 2))
approximativ folgende Beziehung zu A hat, welche um so genauer zutrifft,
je kleiner der mit q zu bezeichnende sog. quadratische Mittelfehler
bez. A
, d. i. q = ![]() ist:
ist:
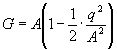 .
(9)
.
(9)
Hiernach kann man G approximativ aus A ableiten.
2) [W. SCHEIBNER, Über Mittelwerte.
Auszug aus einem an Herrn Prof. FECHNER gerichteten Schreiben. Berichte
der Kgl. Sächs. Gesellsch. d. Wissensch. Math.-Phys. Klasse. 1873.
S. 562 flgd.]
Zwischen dem logarithmisch dichtesten Werte D und dem Logarithmus des arithmetisch dichtesten Wertes D besteht folgende Beziehung:
![]() .
(10)
.
(10)
Darin bedeutet e,die untere mittlere logarithmische Abweichung = å l,: m,, Mod den Modulus unseres üblichen logarithmischen Systems = 0,43429, p wie immer 3,14159. Diese Beziehung ist an die Gültigkeit der logarithmischen Verallgemeinerung des G. G. geknüpft und kann daher zu den empirischen Bewährungen dieser Verallgemeinerung mit benutzt werden.
[Beweis. Der logarithmisch dichteste Wert D bezeichnet dasjenige logarithmische Intervall, das von allen Intervallen der nämlichen Größe die meisten z auf sich vereint. Er wird daher durch das Maximum der Wahrscheinlichkeitsfunktion (4) bei konstantem dl¢und dl,, d. i. durch den Ausgangswert der Abweichungen l ' und l,bestimmt. Der arithmetisch dichteste Wert D dagegen liegt in demjenigen arithmetischen Intervall, das unter allen Intervallen der nämlichen Größe das Maximal - z, besitzt. Man findet daher diesen Wert bei Gültigkeit des logarithmischen Verteilungsgesetzes als das Maximum der auf konstante arith-metische Intervalle bezogenen Wahrscheinlichkeitsfunktion (4). Man bezeichne demgemäß die arithmetischen Abweichungen der a von dem dichtesten Verhältniswerte T durch Q ' = a' - T und Q,= T - a,,so daß dQ' = da' und dQ,= -da, und setze auf Grund der Definitionen l' = log a' -D = log a' - log T ; l,= D - log a, = log T - log a, in den Funktionen (4):
![]()
![]() . (11)
. (11)
Dann erhält man für konstante dQ ' und dQ, zur Bestimmung des Maximums von:
![]() ;
;
![]() .
.
Nun sind aber die l¢ und l,ihrem Wesen nach positiv. Es bietet daher nur die zweite der beiden Gleichungen ein Maximum für:
![]() (12)
(12)
dar. Setzt man hier, um den zu l, gehörigen a-Wert durch D zu bezeichnen:
§ 146. [Zusatz. Wird in Übereinstimmung mit den Ausführungen in § 35 der Grundsatz aufgestellt, daß die Größenänderungen der Exemplare eines K.-G. wesentlich abhängig sind von der Größe der Exemplare, welche die Änderungen erleiden, so ergibt sich unmittelbar die Modifikation, die an der im Zusatz zum XIX. Kapitel (§ 136) entwickelten Hypothese anzubringen ist, um sie dem logarithmischen Verteilungsgesetz dienstbar zu machen.]
[Es können nämlich zur Ableitung des logarithmischen Gesetzes ebenso wie zur Ableitung des arithmetischen besondere Einflüsse oder Umstände, kurz Kräfte als Ursachen der Größenänderungen vorausgesetzt werden. Ihre Anzahl ist unbestimmt groß, gleich n anzunehmen und allen in gleicher Weise die W. p für ihr Eingreifen, die W. q = 1 p für das Ausbleiben ihrer Wirkung zuzuschreiben. Der Erfolg ihres Auftretens ist nun aber nicht mehr als ein additiv hinzutretender Zuwachs, sondern als eine Vervielfachung aufzufassen, so daß an Stelle von a + i und a + xi vielmehr ai und aix tritt. Man erhält somit auf Grund dieser Modifikation für ein Exemplar von der Größe aix die nämliche W., die der früher entwickelten Hypothese zufolge einem Exemplare von der Größe a + xi zukam, so daß nunmehr:
![]() .
(13)
.
(13)
Setzt man aber a= log a und i = log i , so wird a+ xi = log (aix),und man erhält als Ausdruck für die W., daß der Logarithmus der Größe eines Exemplares gleich a+ xi sei:
![]() .
(14)
.
(14)
Hiernach gelten die früheren Entwicklungen in der nämlichen Weise und in dem nämlichen Umfange für das logarithmische Verteilungsgesetz , wenn nur überall a durch a= log a und i durch i = log i ersetzt wird.]