![]() .
(1)
.
(1)
§ 137. Zu den gewöhnlich berücksichtigten Elementen eines K.-G. gehören die extremen Werte, welche die Verteilungstafel desselben bietet, d. i. das Maß des größten und kleinsten Exemplares; auch hat es ein mehrfaches Interesse, sich damit zu beschäftigen. Schon aus bloßer Kuriosität kann man sich dafür interessieren, wie groß der größte Riese und der kleinste Zwerg ist, die in einem gegebenen Lande oder überhaupt vorgekommen sind, welches die größte Hitze oder Kälte ist, bis zu der die Temperatur an einem gegebenen Orte angestiegen und herabgesunken ist, u. s. w. Aber die Angabe der extremen Werte eines untersuchten Gegenstandes hat auch einen wissenschaftlichen Wert für die Kenntnis desselben, indem sie mit Rücksicht auf die Zahl der Exemplare, unter welchen diese Extreme beobachtet sind, zur Charakteristik desselben beiträgt; auch kann die nach den beobachteten Extremen gestellte Erwartung, zwischen welchen Grenzen ein künftiges Exemplar zu suchen sein wird, worüber hinaus es voraussetzlich nicht steigen, worunter es nicht sinken wird, mitunter praktisch werden. So kann der höchste zu erwartende Wasserstand eines Flusses die Höhe des schützenden Dammes oder die Höhe von Anlagen an seinen Ufern bestimmen, die größte zu erwartende Kälte eine Grenze für die Anpflanzung gewisser Gewächse setzen, u. s. w.
Man darf nur nicht vergessen, daß die Größe der Extreme mit abhängig von der Zahl der Exemplare ist, welche der Beobachtung unterliegen, und wenn z. B. die Höhe eines Flusses binnen 100 Jahre ein gewisses Maß nicht überstiegen hat, so kann man nicht darauf rechnen, daß es nicht in 1000 Jahren einmal der Fall sein sollte, da hiermit größerer Spielraum zur Entwicklung der Extreme geboten wird, woraus sofort das Interesse einleuchtet, ein Gesetz der Abhängigkeit der Größe der Extreme von der Zahl der Exemplare zu finden, ein Interesse, was mit dem praktischen zugleich ein wissenschaftliches ist. Unmittelbar hat jede empirische Bestimmung der Extreme nur für die Zahl von Exemplaren Bedeutung, aus welcher die Bestimmung erfolgt ist; kann aber mit zu den empirischen Unterlagen für die allgemeine Bestimmung der Extreme mit abgeänderter Zahl dienen.
Bisher hat man diesen Punkt mehrfach übersehen, indem ich an mehr als einem Orte die Größe der absoluten oder relativen Abweichung zwischen den Extremen: E' - E,oder (E' - E,) : A , die aus verschiedenen m bei verschiedenen K.-G. erhalten wurden, zum Vergleiche der absoluten oder relativen Variabilität der betreffenden Gegenstände verwendet finde, was ganz irrige Folgerungen mitführen kann.
Hierbei scheint das Apercu zu Grunde gelegt, daß, wenn man nur die Extreme aus einer großen Zahl bestimme, man darauf rechnen könne, wenn nicht die absolut möglichen Extreme, doch solche, die sich ihnen sehr nähern, zu erhalten, und in Ermangelung anderen Anhaltes sich bei den gefundenen begnügen könne. Aber diese Annahme einer approximativ erreichbaren Grenze der Extreme bei wachsendem m hat weder empirisch, noch theoretisch etwas für sich; sondern wahr ist nur nach beiden Gesichtspunkten, daß die Größe der Extreme in sehr viel kleinerem Verhältnisse als die Größe des m wächst, aber, wenn m bis ins Unendliche steigend gedacht wird, immer in angebbarer Weise mit fortwächst.
§ 138. [Indessen steht der Aufstellung einer gesetzlichen Beziehung zwischen der Größe der Extreme und der Anzahl der Werte, unter denen die Extreme vorkommen, eine beispielsweise von DOVE und von ENCKE vertretene Auffassungsweise entgegen, der zu folge die Extreme jedweder Gesetzlichkeit sich entziehen würden.]
DOVE, nachdem er in seiner ersten,
"die geographische Verbreitung gleichartiger Witterungserscheinungen" betreffenden
Abhandlung1) : "Über die nicht periodischen
Änderungen der Temperaturverteilung auf der Oberfläche der Erde",
die extremen Abweichungen angegeben, welche von monatlichen und jährlichen
Temperaturmitteln während einer gegebenen Anzahl Jahre an verschiedenen
Beobachtungsorten stattgefunden, bemerkt ausdrücklich: "die hier gegebenen
Zahlen haben noch etwas sehr Willkürliches, da ein einziger ungewöhnlich
strenger Winter oder ein sehr heißer Sommer die aus einer langen
Reihe vorhergehender Jahre ermittelten Unterschiede vielleicht verdoppeln
kann", eine Bemerkung, der sich auch schmid in seinem großen meteorologischen
Werke2) anschließt. Desgleichen bemerkt
encke in seiner Abhandlung über die Methode der kleinsten Quadrate
3)
auf Grund dessen, daß in den bekannten BESSEL'schen Fehlerreihen
die extremen Beobachtungsfehler etwas zu groß gegen die theoretische
Forderung ausfallen: "übrigens ist diese Abweichung leicht aus dem
Umstande erklärlich, daß größere Fehler in der Regel
eine ganz ungewöhnliche Vereinigung von nachteiligen Einwirkungen
voraussetzen, ja selbst häufig durch ein so isoliert stehendes Ereignis
herbeigeführt werden, daß keine Theorie sie der Rechnung wird
unterwerfen können."
1) Abhandlungen der Kgl. Akademie der Wissenschaften zu Berlin, aus
dem Jahre 1848.
2) Lehrbuch der Meteorologie. Leipzig 1860.
3) Berliner Astronom. Jahrbuch für 1834. S.249 flgd.
Demgemäß ist in der Tat bisher weder von einer theoretischen, noch erfahrungsmäßigen Untersuchung und Feststellung gesetzlicher Verhältnisse dieser Werte die Rede gewesen, und so dürfte nicht nur eine gewisse Lücke in dieser Hinsicht durch die folgende Untersuchung ausgefüllt werden, sondern auch die faktische Beseitigung des Verdachtes, daß die extremen Werte überhaupt keinen gesetzlichen Verhältnissen unterliegen, an sich ein gewisses Interesse in Anspruch nehmen.
Nun ist es allerdings richtig, daß mitunter Extreme oder extreme Abweichungen aus exzeptionellen Ursachen herrühren können, die aus der Reihe der Bedingungen heraustreten, unter welchen ein K.-G. als bestehend aufgefaßt und der Untersuchung unterworfen wird; z. B. faßförmig aufgetriebene oder entschieden mikrocephale Schädel, wo es sich um gesunde Schädel handelt. Solche Extreme sind in der Tat unberechenbar. Aber da sich die aufzustellenden Gesetzmäßigkeiten nur auf solche K.-G. beziehen, die den früher (Kap. IV) angegebenen Requisiten genügen, so kann ein Heraustreten der Extreme aus den gesetzlichen Beziehungen geradezu als ein Anzeichen dafür gelten, daß diese Extreme abnorm sind, die, wo es sich um normale Verhältnisse handelt, auszuschließen sind.
§ 139. Empirisch kann man sich von der Änderung der Extreme mit der Größe des m leicht in folgender Weise überzeugen.
Man bestimme aus der Totalität einer Urliste von gegebenem m , in welcher die Maße in zufälliger Ordnung enthalten sind, die beiden Extreme E' und E,, teile dann ohne Änderung der zufälligen Ordnung der Maße die Gesamtheit derselben in eine Anzahl von gleichen Fraktionen z. B., wenn das totale m = 1000 wäre, in 10 Fraktionen von je m = 100, und bestimme nun auch die Extreme dieser Fraktionen. Wenn nicht zufälligerweise, was doch bei großem Total - m nur ausnahmsweise der Fall sein kann, dieselben Extreme schon in der Totalität mehrfach vorkommen, wird man sie in den Fraktionen nicht wiederfinden, sondern diese werden durchschnittlich nur kleinere E' und größere E,geben; und wiederholt man an jeder Fraktion von m = 100 das Verfahren, indem man sie z.B. in 10 Fraktionen von m = 10 teilt, so wird natürlich der entsprechende Erfolg eintreten. Nun kann man die Totalität der Maße von gegebenem m , die man zuerst vor sich hatte, selbst als Fraktion einer Totalität von größerem m betrachten und schließen, daß, wenn man mehrere solcher Fraktionen von demselben m vor sich hätte, die E' und E,, die man aus denselben erhält, auch durchschnittlich von dem E' und E,der größeren Totalität aller Exemplare in Plus und Minus überboten werden würden.
Man kann bemerken, daß die E , welche aus den gleichzahligen Fraktionen derselben Totalität erhalten werden, eine etwas abweichende Größe haben, und indem man die Totalität selbst als eine Fraktion unter anderen gleichzahligen Fraktionen einer größeren Totalität mit gegebenem m betrachten kann, würde man noch zwischen den E dieser größeren Fraktionen Verschiedenheiten finden, so daß man also überhaupt nicht darauf rechnen kann, ein von gegebenem m abhängiges ganz bestimmtes E' und E,zu finden; wohl aber kann man erstlich bestimmt sagen, daß normalerweise in dem oben dafür eingeführten Sinne die von gegebenem m abhängigen E durchschnittlich um so weiter in + steigen und in - abnehmen, je größer m ist; zweitens kann man ihre Variation bei gegebenem m als Sache einer Unsicherheit wegen unausgeglichener Zufälligkeiten, die sich einer näheren Untersuchung fügt, betrachten, worauf unten zurückzukommen.
Erläutern wir das Vorige an der
Studentenmaßtafel4) mit m = 2047
, deren Elemente in § 65 gegeben sind, wonach
A1
der primären Tafel = 71,77; Dp
nach Reduktion auf i = 1 Zoll aber im Mittel von 4 Lagen = 71,96
ist. Da jedoch die Benutzung des ganzen m = 2047 ungeheuer
umständlich sein würde, benutze ich nur 360 Werte wie folgt.
4) Wegen des Nachteils
der ungleichförmigen Schätzung, welchem die Rekrutenmaße
überhaupt unter-liegen, würde ich lieber ein anderes Beispiel
gewählt haben, wenn mir Urlisten von anderen Gegenständen mit
gleich sicherer reiner Zufälligkeit in der Folge der Maßgrößen
zu Gebote gestanden hätten; doch kann jener Nachteil die Verhältnisse,
auf die es folgends ankommt, unstreitig nur unwesentlich benachteiligen.
Aus der Urliste, in welcher die Maße sich ganz zufällig folgen, wurden von jedem der 20 Jahrgänge die ersten 18 Maße in ihrer zufälligen Folge ausgeschrieben und zur Totalität von 360 Maßen vereinigt. Hierin wurde E¢ = 77,5 , E,= 64 Zoll gefunden. Hiernächst wurden diese 360 Maße in 180 Fraktionen mit einem m = 2 geteilt, in deren jeder natürlich das eine Maß unmittelbar, als E¢, das andere als E,auftritt, und durch Division der Summe der so erhaltenen E' und E,mit 180 wurden das mittlere E' = 73,16 und mittlere E,= 70,26 erhalten; weiter wurde eine Teilung der 360 Maße in 120 Fraktionen mit einem m = 3 vorgenommen, deren mittleres E' und E,berechnet u. s. f. wovon die Resultate in folgender Tabelle zusammengestellt sind.
I. Mittelwerte der oberen und unteren Extreme aus n Fraktionen mit je m Gliedern.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 72 |
|
|
|
|
|
|
|
|
|
|
|
|
Diese Tabelle gibt zu folgenden Bemerkungen Anlaß.
Ausnahmslos sieht man mit wachsendem m die mittleren E' steigen, die E,abnehmen, wovon die natürliche Konsequenz ist, daß der Unterschied zwischen beiden Extremen E' - E,mit wachsendem m wächst, nur, wie man sieht, nichts weniger als proportional mit m wächst, indem er z. B. bei m = 2 gleich 2,9 , bei m = 360 gleich 13,5 ist. Auffällig kann es zunächst scheinen, daß die Summe beider Extreme mit wachsendem m sich nur sehr unbedeutend ändert; und zwar besteht, abgesehen von den kleinen Unregelmäßigkeiten bei m = 4 und 72, welche als Sache unausgeglichener Zufälligkeiten anzusehen, die Änderung in einer kontinuierlichen Abnahme von E' + E,bei wachsendem m . Es ist aber dies so zu verstehen. Natürlich, wenn E' mit wachsendem m wächst, E,abnimmt, ist allgemein gesprochen die Möglichkeit gegeben, daß sich beides gerade kompensiert, wo dann E' + E,bei wachsendem m konstant bleiben müßte, ein Fall, der abgesehen von unausgeglichenen Zufälligkeiten dann zu erwarten, wenn Symmetrie der Abweichungen nach beiden Seiten vom arithmetischen Mittel bestände. Nun nähern sich die Rekrutenmaße einer solchen, da sie aber derselben doch nicht ganz entsprechen, so entspricht auch das Resultat für E' + E,nicht ganz der Voraussetzung einer solchen.
§ 140. [Obschon nun die Werte obiger Tabelle I das Wachsen der oberen Extreme und das Abnehmen der unteren für wachsende m deutlich vor Augen stellen, eignen sie sich doch nicht zur Bewährung der im folgenden (§ 141) aufzustellenden Extremgesetze. Denn diese sind aus dem G. G. abzuleiten, das sich auf die Abweichungen vom arithmetischen Mittel A oder vom dichtesten Werte D bezieht, so daß auch die Extrembestimmungen zunächst die extremen Abweichungen von dem Ausgangswerte und nicht die extremen Werte E' und E,direkt betreffen. Der hierdurch bedingte Unterschied der Bestimmungsweise erhellt aus der Bemerkung, daß E' sehr wohl unterhalb des Ausgangswertes und ein anderes Mal umgekehrt E,oberhalb desselben liegen kann, und daß dann die Abweichung jenes Extrems vom Ausgangswerte nicht sowohl den Maximalwert als vielmehr den Minimalwert der vorkommenden Abweichungen darstellt. Die Durchschnittswerte obiger Tabelle können daher nicht als Durchschnittswerte der extremen Abweichungen gelten, da als solche nur die Maxima der Abweichungswerte in Rechnung zu ziehen sind. Gegen diese Bestimmungsweise läßt sich allerdings der Einwand erheben, daß die Extreme E' und E,als solche, ohne Rücksicht auf den als Ausgangswert gewählten Hauptwert, das Interesse erregen und die Aufstellung direkt gültiger Gesetze verlangen; es kann aber dies nur durch Vermittlung der für die extremen Abweichungen gültigen Gesetze geschehen, da das hierbei zu Grunde zu legende Verteilungsgesetz sich auf Abweichungswerte bezieht. Es sind darum auch zunächst die theoretischen Bestimmungen für die extremen Abweichungen empirisch zu bewähren.]
[Zu diesem Zwecke müssen die Maße der Urliste unter Beibehalten der vorhandenen Reihenfolge durch ihre Abweichungen vom Ausgangswerte ersetzt werden. Ist der letztere der arithmetische Mittelwert A , so treten die Abweichungen D an Stelle der a , und zwar entweder mit oder ohne Scheidung der positiven von den negativen Abweichungswerten, je nach-dem das G. G. nur auf die oberen resp. unteren Abweichungen allein oder auf beide gemeinsam bezogen wird. Beim Ausgange von D dagegen sind die Abweichungen ¶' und ¶,an Stelle der a zu setzen und dabei die positiven ¶' von den negativen ¶, zu sondern, da das zweiseitige G. G., das nunmehr zur Verwendung kommt, prinzipiell die Trennung der oberen von den unteren Abweichungen fordert und auf beide in verschiedener Weise sich bezieht.]
[Im vorliegenden Falle kann man in Anbetracht des schwachen Grades von Asymmetrie, der den Rekrutenmaßen eigen ist, das arithmetische Mittel als Ausgangswert wählen, und zwar sollen mit Rücksicht auf die kleine, zur Verfügung stehende Gesamtzahl von 360 Maßwerten die positiven und negativen Abweichungswerte nicht getrennt behandelt werden. Ich ersetze demgemäß die 360 Rekrutenmaße unter Festhalten ihrer Reihenfolge durch ihre Abweichungen von A , das einfachheitshalber gleich 71,75 statt genauer gleich 71,77 angenommen wurde. Dann enthält die Gesamtheit der Abweichungen eine extreme Abweichung mit dem Werte 7,75 , und jede Unterabteilung derselben weist in gleicher Weise einen und nur einen extremen Abweichungswert auf, der zwar seinem Ursprunge nach entweder positiv oder negativ ist, aber als absoluter Wert auftritt, da die Abweichungen nur ihren absoluten Werten nach in Betracht kommen. Wird nun die Reihe der 360 Abweichungen ganz ebenso wie oben die Reihe der 360 Maße selbst in n Fraktionen, deren jede aus m Werten besteht, zerlegt und jedesmal die allgemein mit U zu bezeichnende extreme Abweichung notiert, so erhält man nachstehende Tabelle, in welcher angegeben wird, wie oft eine Abweichung von bestimmter Größe unter den n Fraktionen als extreme Abweichung U vorkam; dabei sind natürlich für m = 1 die Abweichungen selbst zugleich als extreme Abweichungen genommen:
II. Anzahlen, wie oft die extreme Abweichung U in n Fraktionen mit je m Gliedern vorkam.
|
|
n =360 |
n = 180 |
n = 120 |
n = 90 |
n = 60 |
n = 40 |
|
n = 10 |
|
n = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Diese Reihen, welche Verteilungstafeln für die extremen Abweichungen darstellen, lassen schon durch das sukzessive Vorrücken der kleinsten Werte das Anwachsen der Extreme bei wachsendem m erkennen. Eine genauere Vorstellung hiervon gewährt jedoch folgende Zusammenstellung von mittleren Werten der U , als welche das arithmetische Mittel Ua, der Zentralwert Ucund der dichteste Wert Uddienen sollen:
III. Die mittleren Werte Ua, Ucund Ud der extremen Abweichungen aus m-gliedrigen Fraktionen.
|
|
|
|
|
|
|
|
|
|
|
|
| Ua |
|
|
|
|
|
|
|
|
|
|
| Uc |
|
|
|
|
|
|
|
|
|
|
| Ud |
|
|
|
|
|
|
|
|
|
|
Hierzu ist zu bemerken, daß Ucdurch einfache Interpolation, Udaber als derjenige Wert bestimmt wurde, auf den die größte Anzahl der U fiel; nur für m = 6 wurde das Mittel der beiden Werte genommen, die gemeinsam die Maximalzahl 8 besitzen. Von dem unsicher bestimmten dichtesten Werte abgesehen, lassen diese Werte ein ständiges Anwachsen bei wachsendem m bemerken. Doch nimmt auch Ud nicht ab, sondern behält nur zweimal für je drei aufeinanderfolgende m seinen Wert.]
[Hätte man die oberen von den unteren Abweichungen getrennt, statt beide in einer Reihe zu vereinigen, so wären an Stelle der einen Tabelle II zwei Tabellen getreten, die eine für die D' , die andere für die D,; da indessen die Gesamtzahl der Abweichungen für jede einzelne sich etwa auf die Hälfte vermindert hätte, so wäre die Unsicherheit der Bestimmungen wesentlich größer geworden. Hätte man ferner D an Stelle von A als Ausgangswert gewählt, so wäre eine Trennung der Reihe von Abweichungswerten in eine Reihe der ¶' und eine solche der ¶,prinzipiell zu fordern gewesen.]
§ 141. [Um diesen emprischen Werten theoretische Bestimmungen zur Seite zu stellen, ist das Wahrscheinlichkeitsgesetz W[U] abzuleiten, das angibt, mit welcher W. unter m Abweichungswerten der extreme Wert U zu erwarten ist. Soll aber U den extremen Wert darstellen, so muß eine der m Abweichungen jenen Wert haben, während die m - 1 übrigen beliebige Werte zwischen 0 und U annehmen können. Das Gesetz W[U] drückt somit die W. aus, daß von m Abweichungen irgend eine gleich U sei und die übrigen zwischen den Grenzen 0 und U sich halten.]
[Es ist nun, wenn die absoluten Werte der Abweichungen durch Q bezeichnet werden, die W., daß eine Abweichung zwischen die unendlich nahen Grenzen Q und Q+ d Q falle, gleich:
![]() .
(1)
.
(1)
Dabei ist es gleichgültig, ob beim Ausgange vom arithmetischen
Mittel die beiderseitigen Abweichungen + D und
- D oder beim Ausgange vom dichtesten Werte
die einseitigen Abweichungen ¶' resp.
¶,
unter den Q zu verstehen sind; wofern nur im
ersteren Falle h = 1 : h![]() ,im
letzteren Falle h = 1 : e'
,im
letzteren Falle h = 1 : e'![]() resp.
= 1 : e,
resp.
= 1 : e,![]() gesetzt wird, wo h den Mittelwert der D
, e' resp. e,den Mittelwert
der ¶¢resp. ¶,
darstellt.
Soll daher von den m Abweichungen Q1
, Q2 .... Qmbeispielsweise
die erste gleich U und jede folgende kleiner oder höchstens
gleich U sein, so besteht für jene erste die W.:
gesetzt wird, wo h den Mittelwert der D
, e' resp. e,den Mittelwert
der ¶¢resp. ¶,
darstellt.
Soll daher von den m Abweichungen Q1
, Q2 .... Qmbeispielsweise
die erste gleich U und jede folgende kleiner oder höchstens
gleich U sein, so besteht für jene erste die W.:
![]()
und für jede folgende die W.:
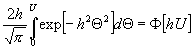 .
.
Die W. für das Zusammentreffen von m Abweichungen, von welchen die erste gleich U ist, und jede folgende einen beliebigen Wert zwischen 0 und U besitzt, ist somit gleich:
![]()
Eben dieser Wert bestimmt jedoch in gleicher Weise dieW., wenn statt der ersten Abweichung eine der folgenden gleich U gesetzt wird, und jedesmal die m - 1 übrigen dem Wertenbereiche zwischen 0 und U angehören. Es wird folglich die W., daß von m Abweichungen irgend eine gleich U sei, und die übrigen zwischen den Grenzen 0 und U sich halten oder mit anderen Worten die W., daß U der extreme Wert unter m Abweichungen sei, durch:
![]() ,
wo t = hU , (2)
,
wo t = hU , (2)
dargestellt. Da
![]() ,
,
![]() ,
,
so kann man auch:
![]() ; (t = hU) (3)
; (t = hU) (3)
setzen.]
[Aus letzterer Darstellungsform ist ersichtlich, daß das Integral über W[U] unmittelbar angebbar ist. Dieses Integral, zwischen bestimmten Grenzen genommen, drückt aber die W. aus, daß die extreme Abweichung zwischen jene Grenzen falle. Es ist daher die W., daß die extreme Abweichung kleiner als U1 = t1: h und größer als U2= t2 : h , gleich:
![]() , (4)
, (4)
so daß insbesondere die W., daß U = t : h die obere resp. untere Grenze der Extreme sei, durch:
![]() resp.
resp. ![]()
bezeichnet wird.]
[Bestimmt man nun einen Wert Uc
= tc : h der
Art, daß
![]() oder
oder ![]() ,
(5)
,
(5)
so ist es gleich wahrscheinlich, bei Bestimmung des Extrems
von m Abweichungen einen größeren oder einen kleineren
Wert als Uc zu
erhalten. Es wird demzufolge Ucden
Zentralwert oder wahrscheinlichen Wert bei vielfach wiederholter Bestimmung
der extremen Abweichung darstellen, dessen Abhängigkeit von m die
Formel (5) angibt, und dessen Zahlenwert für ein gegebenes m mittelst
der t-Tabelle zu finden ist. Aus folgender Zusammenstellung der
zusammengehörigen m und tcfür
einige Werte von m ist das Wachstum dieses Zentral-wertes bei wachsendem
m
zu ersehen.]
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
360 |
|
[Neben dem Zentralwerte ist es von Interesse, denjenigen Wert zu kennen, der als Einzelwert die größte W. besitzt. Er gibt sich bei hinreichend oft wiederholter Bestimmung des Extrems von m Abweichungen als dichtester Wert kund und wird theoretisch als Maximalwert von W[U] bestimmt. Er genügt somit für t = hU der Gleichung:
![]() , (6)
, (6)
und soll durch Ud
= td :
h bezeichnet werden. Die Berechnung von tdaus
der Gleichung (6) für ein vorgelegtes m ist, wie diejenige
von tc ,
mittelst der t-Tabelle vorzunehmen. Man findet so folgende zusammengehörige
Werte von m
und td :
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
360 |
|
Dieselben zeigen, daß td < tc , also auch Ud unterhalb Ucliegt, daß aber bei wachsendem m diese Werte sich einander nähern.]
[Schließlich kann auch der arithmetische Mittelwert der extremen Abweichungen bestimmt werden. Nennt man ihn Ua, so erhält man aus (2):
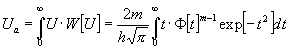 (7)
(7)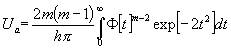 .
(8)
.
(8)
Für m = 1 resultiert aus (7) Ua
= 1 : h![]() d. i. der einfache Mittelwert der Abweichungen selbst. Für m
= 2 gewinnt man aus (8) Ua
=
d. i. der einfache Mittelwert der Abweichungen selbst. Für m
= 2 gewinnt man aus (8) Ua
= ![]() :
h
:
h![]() ,
d. i. den mit
,
d. i. den mit ![]() =
1,4142 multiplizierten Mittelwert der Abweichungen selbst. Für größere
m
kann
F [t] nach § 118 in Reihenform dargestellt
und somit auch Ua in eine
Reihe entwickelt werden. Beispielsweise gelangt man auf diesem Wege für
m
= 3 zu:
=
1,4142 multiplizierten Mittelwert der Abweichungen selbst. Für größere
m
kann
F [t] nach § 118 in Reihenform dargestellt
und somit auch Ua in eine
Reihe entwickelt werden. Beispielsweise gelangt man auf diesem Wege für
m
= 3 zu:
![]()
oder, da
![]() ,
,
zu:
![]() .
.
Es wird somit Ua gleich dem mit 1,6623 multiplizierten Mittelwerte der Abweichungen selbst.]
[Jeder einzelne von den drei Werten Uc , Ud und Uastellt in besonderer Weise die Abhängigkeit der extremen Abweichungen von der Anzahl m der Abweichungen, aus welchen die Bestimmung erfolgt, vor Augen. Es ist jedoch, wenn es gilt, die theoretischen Werte mit den empirischen zu vergleichen, ebensowohl die Sicherheit der empirischen Bestimmung als auch die Leichtigkeit der theoretischen Berechnung zu berücksichtigen und mit Rücksicht hierauf zu erwägen, welcher von den drei Werten den größten Vorteil bietet. Nun ist die Berechnung des theoretischen Wertes von Ucbequemer als diejenige von Ud oder von Ua, bezüglich der empirischen Bestimmung steht aber Ud hinter Uc und Ua an Sicherheit zurück, während Uc und Ua im allgemeinen gleiches Zutrauen verdienen. Man wird sich daher mit Vorteil des Zentralwertes Uc zum Vergleiche der Theorie mit der Erfahrung bedienen.]
[Für die Rekrutenmaße, für
welche die empirisch bestimmten Werte von Ucin
Tab. III verzeichnet sind, führt dieser Vergleich zu folgenden Resultaten,
wobei der Mittelwert
h der einfachen Abweichungen
nach § 65 gleich 2,045 , also 1: h =
h![]() =
3,625 gesetzt ist:
=
3,625 gesetzt ist:
IV. Vergleich der theoretischen Werte von Ucmit den empirischen, aus m-gliedrigen Fraktionen bestimmten.
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
0 |
9
|
|
|
|
|||
|
|
|
|
|
18
|
|
|
|
|||
|
|
|
|
|
36
|
|
|
|
|||
|
|
|
|
|
72
|
|
|
|
|||
|
|
|
|
|
360
|
|
|
|
|||
Man wird, insbesondere in Anbetracht der geringen Anzahl von 360 Werten, die der empirischen Bestimmung unterliegen, die Übereinstimmung der theoretischen und empirischen Werte ohne Zweifel befriedigend finden, so daß hiernach das aufgestellte Wahrscheinlichkeitsgesetz durch die Erfahrung bestätigt wird.]
§ 142. [Die wichtigsten Folgerungen aus den vorstehenden Entwicklungen sind diese:
l) Ist ein K.-G. mit wesentlicher Asymmetrie
wie als Regel vorauszusetzen vorgelegt, und hat das zweiseitige G.
G. für denselben Geltung, so besteht, wenn t' = U' :
e'![]() gesetzt
wird, die W.:
gesetzt
wird, die W.:
![]() (9)
(9)
dafür, daß der extreme Wert der m' oberhalb D gelegenen Abweichungen gleich U' und mithin das obere Extrem selbst gleich:
![]() (9a)
(9a)
sei. In entsprechender Weise besteht die W.:
![]() (10a)
(10a)
sei. Ist es nun möglich, in fortgesetzter Wiederholung immer wieder m' oberhalb und m,unterhalb D gelegene Exemplare des vorliegenden K.-G. nach Zufall auszuwählen, so wird der Zentralwert der auf diese Weise entstehenden oberen und unteren Extreme durch:
![]() ; wo
; wo ![]()
![]() ; wo
; wo ![]() (11)
(11)
der dichteste Wert durch:
![]() ; wo
; wo ![]()
![]() ; wo
; wo ![]() (12)
(12)
der arithmetische Mittelwert durch:
![]() ; wo
; wo 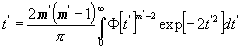
![]() ; wo
; wo 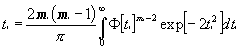 (13)
(13)
sich darstellen lassen.]
[2) Da mit wachsenden m' und m,die ihnen nach obigen Formeln zugehörenden Werte t' und t,wachsen, so besitzen zunächst die Differenzwerte t' - t,und m' - m' gleiches Vorzeichen; da ferner nach dem Proportionalgesetze auch e' - e,das gleiche Vorzeichen wie m' - m,hat, so gilt dasselbe von den Differenzen e't' - e,t, und m¢- m,. Die Asymmetrie der extremen Abweichungen bez. D hat somit die nämliche Richtung wie die Asymmetrie der Abweichungszahlen bez. D . Will man dieses Gesetz auf die Abweichungen bez. des arithmetischen Mittels A übertragen, so gelangt man zu dem in § 33 unter 7) an zweiter Stelle angegebenen Umkehrgesetze auf Grund folgender Überlegung. Da die extremen Abweichungen groß sind und relativ großen Schwankungen unterliegen, ist die Annahme gestattet, daß die Differenz der Abweichungen ihr Vorzeichen nicht ändere, wenn man von D zu dem relativ nahen Werte A übergeht. Die Differenz der Abweichungszahlen bez. A hat aber das entgegengesetzte Vorzeichen wie die Differenz der Abweichungszahlen bez. D . Es hat somit, sofern jene Annahme zutrifft, der Unterschied der extremen Abweichungen bez. A das entgegengesetzte Vorzeichen wie der Unterschied zwischen den Abweichungszahlen bez. A . In der Tat findet dieses Umkehrungsgesetz z. B. in den Tabellen III und IV des XXV. Kapitels für die Glieder der Roggenhalme (mit nur einer Ausnahme unter 15 verschiedenen Fällen) seine Bewährung. Dasselbe kann jedoch bloß als ein empirisches Gesetz gelten, das für den Fall wesentlicher Asymmetrie in der Regel zutrifft. Bei unwesentlicher Asymmetrie hingegen dürfte es seine Geltung nicht mehr behaupten (vergl. § 181.)]
[3) Verschwindet die Asymmetrie des
K.-G., so sind auch für die extremen Abweichungen prinzipiell gleiche
Werte zu fordern, als deren Ausgangswert nunmehr das mit D zusammenfallende
A
unter Beiziehung des einfachen G. G. an Stelle des zweiseitigen zu
gelten hat. Für diesen Fall bleiben die unter 1) angegebenen Formeln
bestehen, wenn nur m' und
m,
durch
½m und
e' sowie e,durch
das für beide Seiten in gleicher Weise gültige hersetzt
wird. Da sich aber für wesentliche Symmetrie das Verteilungsgesetz
bei Zugrundelegen des Gesamt-m auf beide Seiten von A gemeinsam
bezieht, so ist es zutreffender, die positiven und negativen Abweichungen
gemeinsam der Extrembestimmung zu unterwerfen, was zu fol-genden Aufstellungen
führt. Setzt man t = U : h![]() ,so
besteht die W.:
,so
besteht die W.:
![]() (14)
(14)
dafür, daß der extreme Wert der Abweichungen ± D bez.. A gleich U sei. Es bleibt jedoch unentschieden, ob U im positiven oder im negativen Sinne dem Ausgangswerte beizufügen sei. Es läßt sich daher nur sagen, daß alsdann entweder
![]() oder
oder ![]() (14a)
(14a)
ist, und zugleich im ersteren Falle E,oberhalb
A
U , im letzteren Falle E' unterhalb
A + U
bleibt.
Entsprechende Bemerkungen sind auch bezüglich der Hinzufügung
der gemäß den Formeln (5), (6) und (8) zu bestimmenden mittleren
extremen Abweichungswerte Uc ,
Ud und Uazum
Ausgangswerte zu machen. Denn man erhält hierdurch nicht die mittleren
Extreme selbst, sondern nur eine obere resp. untere Grenze für das
obere resp. untere mittlere Extrem.]