![]()
![]() .
(1)
.
(1)
§ 129. [In den beiden vorhergehenden Kapiteln wurde das G. G. so weit entwickelt, daß es als geeignetes Instrument für die Verteilungsrechnung der K.- G. ebensowohl bei wesentlicher Symmetrie als bei wesentlicher Asymmetrie der Abweichungen zur Benutzung bereit steht. Da nun die Erfahrung lehrt, daß in der Tat das GAUSS'sche Fehlergesetz bei geringer Schwankung der Einzelwerte um ihren Mittelwert das zutreffende Verteilungsgesetz darstellt, und daß selbst bei schwacher Asymmetrie, bei der es zweifelhaft bleibt, ob nur eine Störung wesentlicher Symmetrie oder wesentliche Asymmetrie vorliegt, das zweiseitige Gesetz Vorteile dem einfachen Gesetze gegenüber gewährt, so kann man das zweiseitige G. G. als das hinreichend sich bewährende Verteilungsgesetz der K.-G. mit schwacher verhältnismäßiger Schwankung aufstellen. Dieses Grundgesetz der Verteilung für K.-G. stützt sich alsdann lediglich auf die Erfahrung und bedarf keiner theoretischen Begründung. Es bleibt daher vom empirischen Standpunkte aus bloß noch die Aufgabe, die bereits früher (im V. Kap.) vorgreiflich aufgeführten Spezialgesetze wesentlich asymmetrischer Verteilung als Folgerungen des Grundgesetzes abzuleiten.
[Wenn aber auch dieses Grundgesetz durch die Erfahrung hinlänglich gestützt wird, so ist es doch wohl von Interesse, theoretische Voraussetzungen betreffs der K.-G. zu entwickeln, um das zweiseitige G. G. in ähnlicher Weise, wie es für das einfache Gesetz in der Fehlertheorie geschehen ist, theoretisch zu begründen. Dies soll nach Ableitung der Spezialgesetze in dem Zusatze zu diesem Kapitel geschehen.]
§ 130. [Die Spezialgesetze wesentlich asymmetrischer Verteilung zerfallen in zwei Gruppen. Die erste enthält Bestimmungen des Ausgangswertes, denen zufolge letzterer
1) [Außer diesen Gesetzen wurden in § 33 auch
noch die Extremgesetze aufgeführt. Dieselben haben jedoch ebensowohl
bei Symmetrie als bei Asymmetrie der Abweichungswerte Geltung und sind
somit keine Gesetze wesentlich asymmetrischer Verteilung. Da sie
überdies zu ausführlicheren Erörterungen Anlaß geben,
so werden sie im folgenden Kapitel eine besondere Behandlung erfahren.]
[Zur Ableitung dieser Gesetze ist das zweiseitige G. G. zu Grunde zu legen, das als Verteilungsgesetz der Exemplare eines K.- G. folgende Form erhalten soll:
![]()
![]() .
(1)
.
(1)
Hier bedeuten, wie üblich, m¢
und m,die
Anzahlen der oberhalb und unterhalb des Ausgangswertes D gelegenen
Abweichungen, ¶' und ¶,
die
ihrem absoluten Werte nach genommenen Abstände der Abweichungen von
D
, h' und h,schließlich
die reziproken Werte von e' ![]() und e,
und e,![]() wo
e'
und e,die Mittelwerte der ¶'
und ¶,sind.
Es soll aber dabei der Ausgangswert D nicht von vornherein als dichtester
Wert noch auch als der durch das Proportionalgesetz bestimmte Wert gelten,
da ja beide Eigenschaften erst bewiesen werden sollen. Es ist vielmehr
D
als ein vorerst willkürlich gewählter Ausgangswert anzusehen,
der erst auf Grund des Gesetzes (1) als der mit jenen beiden Eigenschaften
behaftete Wert nachzuweisen ist. Noch ist zu bemerken, daß
z
' und z,keine
Anzahlen bedeuten, sondern bei geometrischer Interpretation nur die zu
¶'
resp.
¶,als Abszissen
gehörigen, auf letzteren senkrecht stehenden Ordinaten des Verteilungsgesetzes
vorstellen. Die Anzahlen der Abweichungen dagegen beziehen sich stets auf
Intervalle und werden durch Flächenstreifen repräsentiert, so
daß die Gleichungen
wo
e'
und e,die Mittelwerte der ¶'
und ¶,sind.
Es soll aber dabei der Ausgangswert D nicht von vornherein als dichtester
Wert noch auch als der durch das Proportionalgesetz bestimmte Wert gelten,
da ja beide Eigenschaften erst bewiesen werden sollen. Es ist vielmehr
D
als ein vorerst willkürlich gewählter Ausgangswert anzusehen,
der erst auf Grund des Gesetzes (1) als der mit jenen beiden Eigenschaften
behaftete Wert nachzuweisen ist. Noch ist zu bemerken, daß
z
' und z,keine
Anzahlen bedeuten, sondern bei geometrischer Interpretation nur die zu
¶'
resp.
¶,als Abszissen
gehörigen, auf letzteren senkrecht stehenden Ordinaten des Verteilungsgesetzes
vorstellen. Die Anzahlen der Abweichungen dagegen beziehen sich stets auf
Intervalle und werden durch Flächenstreifen repräsentiert, so
daß die Gleichungen
![]()
![]() (3)
(3)
bezeichnet.]
[Durch die Gleichungen (1) ist für jeden endlichen Wert von ¶' und ¶,der zugehörige Wert von z ' und z, und damit auch der zugehörige Wert von z' und z,oder von W¢ und W, in eindeutiger Weise bestimmt. Für den Ausgangswert selbst jedoch, dem die Abweichungswerte ¶' = 0 und ¶,= 0 zugehören, fehlt diese Eindeutigkeit, es sei denn, daß
![]() ;
; ![]() (5)
(5)
so, daß ein ununterbrochener Übergang der beiden Kurvenzüge, welche die Gleichungen (1) darstellen, in der Tat nur bei Erfüllung der Bedingungsgleichung (4) stattfindet. Daß aber diese Bedingungsgleichung notwendig erfüllt werden muß, erhellt aus folgender Überlegung.]
[Es ist selbstverständlich, daß einem Intervalle von gegebener Größe und gegebener Lage nur eine ganz bestimmte Anzahl von Abweichungen angehören kann. Dies hat zur Folge, daß auch einem unendlich kleinen Intervalle, das als Grenze eines endlichen Intervalles zu betrachten ist, die nämliche Anzahl zukommen muß, mag es als Grenze eines in den oberen oder eines in den unteren Teil der Verteilungstafel sich erstreckenden Intervalles angesehen werden. Ist aber für den Ausgangswert z' verschieden von z,, so ist auch die Anzahl der Abweichungen für das dem Ausgangswerte zugehörige Intervall davon abhängig, ob das letztere von Seiten der oberhalb oder von Seiten der unterhalb des Ausgangswertes gelegenen Abweichungen erreicht gedacht wird. Da dies nicht zulässig ist, so muß z ' = z, sein und somit die Bedingungsgleichung (4) erfüllt werden.]
[Untriftig wäre es, dem entgegenzuhalten, daß man so zwar für die Anzahlen, nicht aber für die W. der Abweichungen die Eindeutigkeit erziele. Denn die Wahrscheinlichkeitsbestimmungen (3) beziehen sich auf jede Seite der Abweichungen besonders, ohne dabei die andere Seite zu berücksichtigen oder von ihr in Mitleidenschaft gezogen zu werden. Will man eine beide Seiten gemeinsam berücksichtigende Bestimmung der W., so muß dieselbe auf die Gesamtanzahl m = m¢ + m,der Abweichungen Bezug nehmen, und es ist alsdann zu setzen:
![]()
![]() , (6)
, (6)
so daß, wie es sein muß, für ¶' = ¶,= 0 die Eindeutigkeit der Wahrscheinlichkeitsbestimmung auf Grund von (4) sich ergibt.]
[Es ist somit bei Aufstellung des Verteilungsgesetzes (1) die Bedingungsgleichung (4) beizufügen. Damit wird aber von dem Ausgangswerte die Erfüllung des Proportionalgesetzes
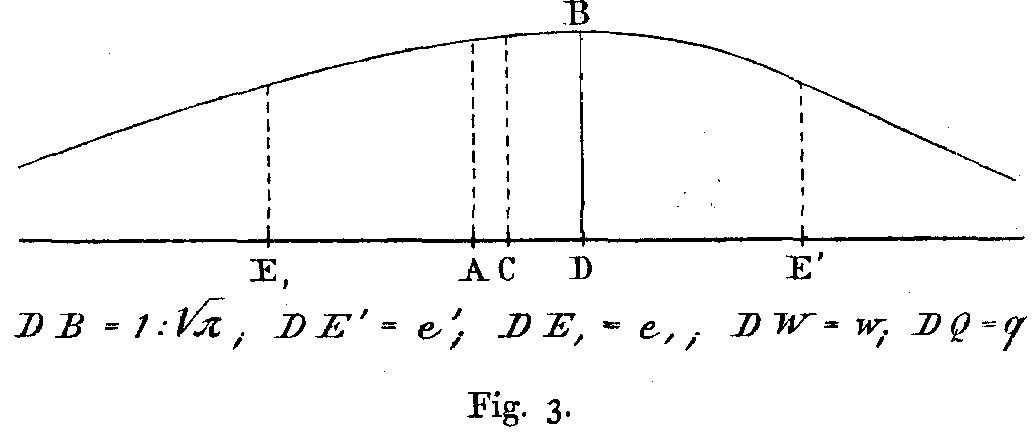
[Zur Veranschaulichung dieses Verteilungsgesetzes mögen die beiden folgenden Kurvenzüge dienen, von welchen der erste den Verlauf der oberhalb D gelegenen Werte mit Angabe der wahrscheinlichen und mittleren Abweichungen w = DW ; e' = DE' ; q = DQ ; der zweite den Verlauf der beiderseits von D gelegenen Werte mit Angabe der beiden Haupt-werte A und C neben D und der beiden einfachen mittleren Abweichungen e' = DE' ; e,= DE, vor Augen stellt.
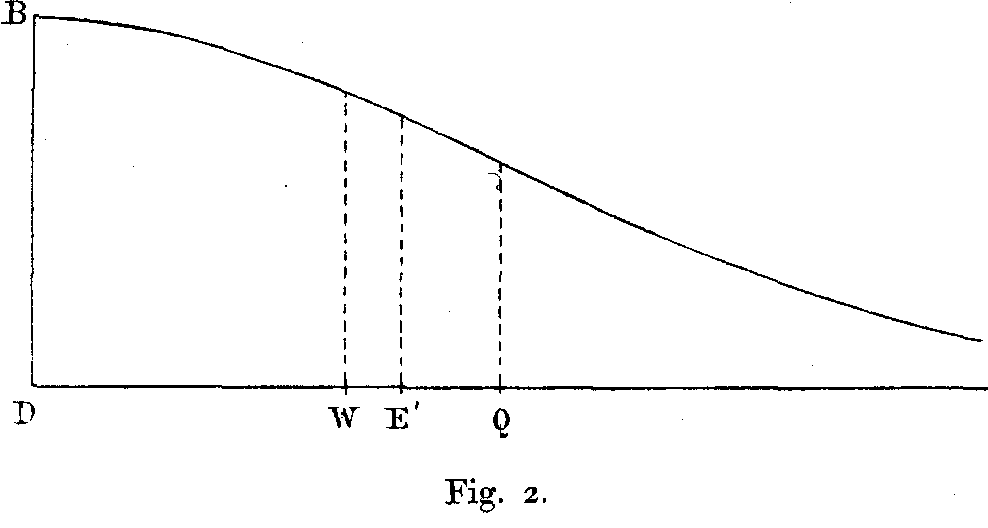
§ 131. [Nur ausnahmsweise werden die Anzahlen m' und m,der oberhalb und unterhalb des Ausgangswertes D gelegenen Abweichungen einander gleich sein. In diesem Ausnahmefalle liegen der Zentralwert C und der arithmetische Mittelwert A mit D vereint. Denn es ist ja m' = m,,so daß die den Zentralwert charakterisierende Bedingung erfüllt ist; aus der Gleichheit von m' und m,folgt aber weiterhin auf Grund des Proportionalgesetzes, daß auch e' = e,und mithin m'e' = m,e,. Dies besagt, daß auch die beiderseitigen Abweichungssummen einander gleich sind, wodurch der arithmetische Mittelwert bestimmt wird.]
[Ist jedoch, wie in der Regel vorauszusetzen, m' von m,verschieden, so liegen die beiden Hauptwerte A und C niemals mit D vereint, und es lassen sich ihre Abstände von D aus dem G. G. wie folgt ableiten.]
[Man bezeichne die größere der beiden Anzahlen m' und m,durch m", die kleinere durch m" und kennzeichne die auf Seite der m" liegenden Werte ¶ , e , h und t im Einklange mit den früher (§ 33) getroffenen Bestimmungen durch zwei Strichelchen oben. Dann ist der Zentralwert C als derjenige Wert zu suchen, der im Vereine mit D ein Intervall abgrenzt, das ½ (m" - m") Abweichungen enthält; denn es ist:
![]() , (8)
, (8)
so daß oberhalb und unterhalb des der Art bestimmten Wertes gleich viel Abweichungen liegen, wie es für den Zentralwert zu fordern ist. Aus dem Verteilungsgesetze folgt aber, wenn g = C D den Abstand der Werte C und D ohne Rücksicht auf ihre gegenseitige Lage angibt:
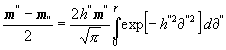 ,
(9)
,
(9)
oder, wenn h" ¶¢ ' = t; h"g = t" gesetzt wird:
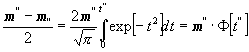 . (10)
. (10)[Der Abstand C D ist demnach wesentlich von dem Quotienten (m"- m") : m'' abhängig. Ist der letztere gleich Null, so wird auch g gleich Null, und C fällt, wie schon bemerkt, mit D zusammen. Ist jedoch dieser Quotient zwar nicht gleich Null, wohl aber hinreichend klein, so daß seine zweite Potenz vernachlässigt werden kann, so ist es erlaubt, F [t"] als Größe der nämlichen Ordnung angenähert durch:
![]() oder
oder ![]() (12)
(12)
darzustellen und mithin:
![]() (13)
(13)
oder:
![]() (14)
(14)
zu setzen. Andererseits erreicht C D den größtmöglichen Wert, wenn (m" - m"):m" den Wert 1 annimmt, d. h. wenn m" = 0 und m" = m , wenn also die Gesamtheit der Abweichungen auf einer und derselben Seite des Ausgangswertes liegt, und die Asymmetrie infolgedessen unendlich groß wird. Es wird in diesem Grenzfalle aus (10) die einfachere Gleichung:
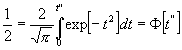 , (15)
, (15)
so daß t" = w : e"![]() ,
wo w den wahrscheinlichen Wert der Abweichungen darstellt, der nach
§ 119 gleich 0,845347 × e" zu
setzen ist. Für den Abstand C D erhält man sonach die
Gleichung:
,
wo w den wahrscheinlichen Wert der Abweichungen darstellt, der nach
§ 119 gleich 0,845347 × e" zu
setzen ist. Für den Abstand C D erhält man sonach die
Gleichung:
[Beachtet man nämlich, daß die größere der beiden Abweichungssummen å¶' und å¶, infolge des Proportionalgesetzes auf der nämlichen Seite von D sich findet, auf der die größere der beiden Abweichungszahlen, nämlich m" , zu suchen ist, wonach die größere der beiden Summen durch å¶", die kleinere durch å¶" bezeichnet wird, so kann man setzen:
å¶"= m"D - å a" .(17)
![]() ,
,
die Gleichung:
![]() , (18)
, (18)
die jedoch die Eigenschaft von D , das Proportionalgesetz zu erfüllen, noch nicht berücksichtigt. Zu diesem Zwecke setze man in (18):
å¶" = m"e" ; å¶"= m"e"
![]() ,
(19)
,
(19)
in welcher dem Proportionalgesetze zufolge:
m" e'' - m"e" = 0
ist, so daß schließlich:
A D = e" - e" (20)
resultiert, eine Beziehung, die schon im XI. Kap. aufgestellt wurde, als es sich um die Verwertung der Eigenschaften von Dp im Interesse seiner Bestimmung aus den empirisch gegebenen Tafelwerten handelte.]
[Da nach dem Proportionalgesetze:
![]() (21)
(21)
oder, wenn wie oben:
![]()
gesetzt wird, in die Form:
[Die Bestimmung des Abstandes A D ist somit in der Tat von dem Bestehen des G. G. unabhängig, so daß für jede Verteilungstafel die Gleichung (20) bestehen muß, wenn anders A als Mittelwert und D als Dp, d. i. dem Proportionalgesetz gemäß, berechnet worden sind.]
[Auch für A D lassen sich die Grenzwerte angeben. Ist m" = m", so folgt aus (21), daß auch A = D , im Einklang mit der bereits gemachten Bemerkung, wonach C und A gleichzeitig mit D zusammenfallen. Ist dagegen m" = m und m" = 0 , ist mithin die Asymmetrie unendlich groß, so wird
A D = e" , (23)
also gleich der einfachen mittleren Abweichung, während nach (16) C D die wahrscheinliche Abweichung darstellt. Für den Fall ferner, daß (m" - m") : m¢¢ eine kleine Größe ist, deren zweite Potenz vernachlässigt werden darf, treten die Formeln (12), (13) und (14) in Kraft, so daß aus (21) oder (22) die Gleichung:
![]() (24)
(24)
abgeleitet werden kann.]
§ 132. [Auf Grund obiger Bestimmung
der Abstände C D und A D läßt sich auch
A
C als Differenz der beiden vorigen Abstände finden, wonach die
Abstandsgesetze für die drei Hauptwerte A , C und D
in
folgender Form gegeben werden können:
1) für ganz beliebige Werte m" und m" , d. i. für einen ganz beliebigen Grad der Asymmetrie, hat man nach den Formeln (11) und (20) resp. (22):
A - D = e" - e" = 2F "× e" (25)
A - C = (A - D) - (C D)
= (2 F" - t"![]() )e"
;
)e"
;
2) für m"= 0 und m" = m , d. i. für den Fall unendlich großer Asymmetrie bestehen die Beziehungen (16) und (23); es ist somit:
3) wenn
(m" - m")
:m"
eine kleine Größe vorstellt, deren zweite Potenz vernachlässigt
werden kann, wenn also die Asymmetrie sehr klein ist, kann man nach den
Formeln (14) und (24) setzen:
![]()
![]()
![]() ;
(27)
;
(27)
4) für den Fall, daß gar keine Asymmetrie vorhanden ist, in welchem Falle m' = m, ist, wird schließlich:
A - D = 0 (28)
A - C = 0 .
§ 133. [Aus diesen Abstandsgesetzen lassen sich die Abstandsverhältnisse und insbesondere die p - Gesetze durch Division gewinnen. Man erhält:
1) für den allgemeinen Fall, in welchem der Grad der Asymmetrie keiner Bedingung unterworfen ist:
![]()
![]() (29)
(29)
![]() ;
;
2) für den Fall sehr schwacher Asymmetrie:
![]()
![]() (30)
(30)
![]() ;
;
3) für den Fall unendlich großer Asymmetrie:
![]()
![]() .
.
Die unter 2) und 3) mitgeteilten Werte stellen die Grenzen dar, zwischen welchen die für den allgemeinen Fall geltenden Bestimmungen variieren. Insbesondere sind die für schwache Asymmetrie geltenden Relationen von Interesse, da dieser Fall bei der hier vorauszusetzenden geringen Schwankung der Exemplare der K.-G. so häufig vorkommt, daß er als Regel bezeichnet werden kann. Aus diesem Grunde erhalten die Relationen (30) einen besonderen Namen und heißen die p- Gesetze.]
[Von den drei Quotienten wird gewöhnlich der an erster Stelle stehende berücksichtigt und darum der Einfachheit wegen durch einen besonderen. Buchstaben, nämlich durch p bezeichnet. Es ist somit zu erwarten, daß p oder (C - D) :(A - D) nicht kleiner als 0,785 und nicht größer als 0,845 wird, wofern nicht Unregelmäßigkeiten den Gang der empirischen Werte einer Verteilungstafel stören und die Übereinstimmung mit der Theorie, die allein für die obigen Bestimmungen maßgebend ist, beeinträchtigen.]
§ 134. [Daß C und A auf der nämlichen Seite von D liegen, wurde schon bemerkt; daß aber C zwischen A und D liegt, erhellt aus folgender Darlegung.]
[Nach Formel (29) ist ganz allgemein:
![]() , (32)
, (32)
wo t" der zu F" in der t - Tabelle gehörige Wert ist. Beachtet man nun, daß F" nur Werte zwischen 0 und ½ darstellen kann, da
![]() ,
,
so lehrt ein Blick auf die t - Tabelle, daß durchweg
t" < F " , (33)
denn erst von dem Werte F= 0,6209 ab sind die dreistelligen t -Werte größer als die zugehörigen F - Werte, um bis zum Schlusse der Tabelle größer zu bleiben. Da überdies:
und somit um so mehr:
t¢¢![]() <
2F " ,
<
2F " ,
so ist in der Tat:
C D < A D . (34)
Dies Gesetz, nach welchem C stets zwischen A und D liegt, heißt das Lagengesetz.]
[Das Lagengesetz hat zur Folge, daß die Asymmetrie der Abweichungen bez. D das entgegengesetzte Vorzeichen hat als die der Abweichungen bez. A . Da nämlich bezüglich C die beiderseitigen Abweichungszahlen einander gleich sind, so besteht für jeden Wert oberhalb C die Ungleichung m' < m,und für jeden Wert unterhalb C die Ungleichung m' > m,. Es ist somit, wenn A oberhalb C liegt,
µ¢ < µ, d. h. µ' - µ, negativ.
Dann liegt aber D unterhalb C , so daß:
m¢ > m, d. h. m' - m,positiv ist.
Umgekehrt ist es, wenn A unterhalb und D oberhalb
C
liegt.
Diese Umkehrung der Asymmetrie bezüglich A und
D
wird
das Umkehrgesetz genannt, das mithin ein Ausfluß des Lagengesetzes
ist.]
[Zusatz. Die theoretische Begründung des zweiseitigen GAUSS'schen Gesetzes.]
§ 135. [Bisher wurde das zweiseitige G. G. auf Grund der Erfahrung als das hinreichend sich bewährende Wahrscheinlichkeitsgesetz der K.-G. aufgestellt. Will man nun neben der empirischen Bewährung noch eine theoretische Begründung dieses Gesetzes, so müssen Hypothesen betreffs der K.-G. entwickelt werden, die eine Ableitung jenes Gesetzes gestatten. Die Aufstellung solcher Hypothesen findet ihre Berechtigung eben darin, daß sie zu dem abzuleitenden Gesetze hinführen und dasselbe wie im Keime enthalten. Und wenn auch die Erfahrung allein die Richtigkeit des aufgestellten Gesetzes entscheidet, so wird doch durch eine solche nachträgliche theoretische Begründung die Einsicht in die Natur der K.-G. gefördert.]
[Zunächst weise ich nach, daß es genügt, den nach dem Proportionalgesetze bestimmten Wert Dpals den wahrscheinlichsten Wert vorauszusetzen, um das zweiseitige G. G. in der nämlichen Weise abzuleiten, wie in der Fehlertheorie das einfache G. G. aus der Annahme, das arithmetische Mittel sei der wahrscheinlichste Wert, gefolgert wird. Der Hypothese vom arithmetischen Mittel in der Fehlertheorie steht somit in der Kollektivmaßlehre die Hypothese, daß das Proportionalgesetz den wahrscheinlichsten Wert unter den Exemplaren eines K.-G. bestimme, völlig gleichwertig zur Seite.]
[Um dies zu beweisen, werde angenommen, dass m Exemplare a eines K.-G. vorliegen, für welche ein nach dem Proportionalgesetze bestimmter Wert Dp = a0 existiert. Es liegen dann m,Werte a , nämlich a1 , a2 , , a3 ...., unterhalb Dp und m' Werte a , nämlich a' , a", a"' ..., oberhalb Dp, und es bestellt für die Abweichungen dieser Werte von Dp = a0dem Proportionalgesetze zufolge die Gleichung:
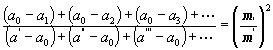
oder, wenn die unteren Abweichungen durch ¶1, ¶2. . . die oberen durch ¶',¶ ", . . . bezeichnet werden:
m'²¶,+ m' ² ¶2+××× + m,2¶' + m,2¶" +××× = 0. (35)
Es mögen nun die W. der Abweichungen ¶1, ¶2××׶ ' , ¶ " × ××durch j (¶1), j (¶2)×××j (¶'), j (¶ ") ×××bezeichnet werden. Dann wird die W. für das Zusammentreffen aller m Abweichungen durch das Produkt der m W., also durch:
![]()
ausgedrückt.]
[Da aber a0 nach der zu Grunde gelegten Hypothese den wahrscheinlichsten Wert darstellen soll, so muß nach den bekannten Prinzipien der Wahrscheinlichkeitsrechnung auch das Produkt der W. für die Abweichungen der vorgelegten Werte a von a0 größer sein als für die Abweichungen von irgend einem anderen, von a0verschiedenen Werte. Es muß daher
![]()
ein Maximum sein. Setzt man nun der Kürze wegen:
![]()
so ist demnach:
![]() (36)
(36)
zu setzen.]
[Diese Gleichung muß mit der Gleichung (35) zugleich bestehen. Bringt man daher (36) in die Form:
![]()
so erhellt, daß:
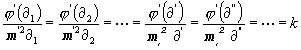 ,
(37)
,
(37)
wo k eine beliebige Konstante ist. Aus:
![]()
folgt aber
![]()
und hieraus durch Integration:
![]() .
(38)
.
(38)
Zugleich erkennt man, daß k einen negativen Wert vorstellen muß, wenn j (¶ ) für ¶ = 0 sein Maximum erreichen soll.]
[Es ist somit für die unterhalb D = a0 gelegenen Abweichungen, die jetzt unterschiedslos durch ¶,bezeichnet werden sollen:
![]() , (39)
, (39)
wo c, eine noch näher zu bestimmende Konstante und - h,² = ½km' 2ist. Für die oberhalb D = a0liegenden Abweichungen dagegen, die unterschiedslos durch ¶' repräsentiert werden mögen, findet man:
![]() , (40)
, (40)
wo wiederum die Bestimmung von c' noch aussteht, während - h¢ ² = ½km,2ist]
[Um schließlich die Konstanten c' und c,zu bestimmen, ist die W., daß von den m' oberen und den m,unteren Abweichungen irgend eine zwischen 0 und ¥ liegt, wie sich von selbst versteht gleich 1 zu setzen. Es muß daher:
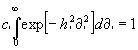
und:
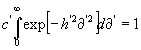
sein. Dies führt, da:
 ,
,
zu:
Daher ist schließlich:
![]()
![]() (42)
(42)
mit der aus den angegebenen Werten für h' und h,folgenden Bedingung :
![]() .]
(42a)
.]
(42a)
§ 136. [Bei dieser Begründung des zweiseitigen G. G. kann es als ein Mangel empfunden werden, daß die zu Grunde gelegte Hypothese des Proportionalgesetzes der Hypothese des arithmetischen Mittels in der Fehlertheorie an Einfachheit und Evidenz nachsteht. Denn man kann zunächst nur in der Erfahrung eine Stütze für dieselbe suchen, wie es denn auch in § 42 als eine fundamentale Tatsache der Erfahrung bezeichnet wurde, daß die K.-G. die Bestimmung eines dichtesten Wertes gestatten, der hinreichend nahe mit dem durch das Proportionalgesetz definierten Werte zusammenfällt.]
[Es ist darum von Interesse, daß eine andere Hypothese aufgestellt werden kann, die sich auf einfache und nahe liegende Überlegungen über die Entstehungsweise der K.-G. stützt. Sie führt vorerst zu einem einheitlichen Verteilungsgesetz; indem jedoch das letztere die Bestimmung eines dichtesten Wertes gestattet, der approximativ dem Proportionalgesetze genügt, stellt sich auch das zweiseitige G. G. als Approximation an jenes einheitliche Gesetz dar. Man gelangt so zu der Erkenntnis, daß die Zweiteilung des Verteilungsgesetzes, wie sie durch die Verwendung des G. G. bedingt ist, nicht durch die Natur der K.-G. gefordert wird, wohl aber durch das Bedürfnis motiviert werden kann, das aus der aufzustellenden Hypothese folgende Gesetz einer bequemen, den Anforderungen der Kollektivmaßlehre genügenden Verwendung zugänglich zu machen.]
[Um die wesentlichen Punkte in der Entwicklung dieser Hypothese klar hervortreten zu lassen, werde zunächst, entgegen den tatsächlich bestehenden Verhältnissen, ein K.-G. vorausgesetzt, dessen Exemplare nur eine kleine Anzahl äquidistanter und endlicher Abstufungen bezüglich der Größe unterscheiden lassen. Beispielsweise mögen fünf Größenstufen existieren, und die Größen selbst der Reihe nach gleich:
a, a + i , a + 2 i , a + 3i , a + 4i (43)
sein. Dann liegt es nahe, die Verschiedenheit der Größe dem Spiele besonderer Kräfte zuzuschreiben, von welchen jede im Falle ihres Wirkens den Zuwachs i erzeugt. Man wird daher vier Kräfte K1, K2, K3, K4 annehmen, der Art, daß jede ebensowohl wirken als auch nicht wirken kann. Tritt keine der vier Kräfte in Wirksamkeit, so entsteht ein Exemplar von der Größe a ; wirkt nur eine der vier Kräfte, so erhält das Exemplar die Größe a + i ; wirken aber zwei, drei oder alle vier Kräfte, so wird die Größe a + 2i , a + 3i oder a + 4i erzeugt. Von der W., die für das Wirksamwerden jeder einzelnen Kraft besteht, wird dann die Häufigkeit des Auftretens der Exemplare einer bestimmten Größenstufe abhängen und hierdurch das Verteilungsgesetz bedingt sein. Man erhält nämlich, wenn die Kräfte unabhängig von einander mit den W. p1, p2, p3 , p4wirken und entsprechend die W. für das Ausbleiben ihrer Wirkung durch q1 = 1 - p1 , q2 = 1 - p2, q3= 1 - p3 , q4 = 1 - p4 angegeben werden, folgende Darstellungen für die W. der verschiedenen Größenstufen:
W[a] = q1q2 q3q4 ;
W[a+i] = p1q2q3q4 + q1 p2q3q4 + q1q2p3 q4 + q1q2q3p4 ;
W[a+2i] = p1 p2 q3 q4 + p1q2p3q4 + p1q2q3p4 + q1p2p3q4+ q1p2q3p4 + q1q2p3p4 ;
W[a+3i] = p1p2 p3q4 + p1p2q3p4 + p1q2p3p4 + q1p2p3p4 ;
W[a+4i] = p1p2p3 p4 . (44)
Hieraus ist zu ersehen, daß eine symmetrische Verteilung der Exemplare auf die verschiedenen Größenstufen nur dann möglich ist, wenn z. B. p1 + p3 = p2 + p4 = 1 , oder wenn für das Auftreten der Wirkung jeder einzelnen Kraft die nämliche W. wie für das Ausbleiben der Wirkung einer der anderen Kräfte besteht. Dann wird:
W[a] = p1p2q1 q2
W[a+i] = (p1p2+q1 q2) (p1 q2+p2q1)
W[a+2i] = (p1p2 +q1 q2)²(p1q2+p2 q1)² -2 p1p2q1q2
W[a+3i] = (p1p2 + q1q2) (p1 q2 + p2 q1)
W[a+4i] = p1p2q1q2
.
Jede andere Bestimmung der W. führt zu einer asymmetrischen Verteilung der Exemplare auf die verschiedenen Größenstufen. Man erhält beispielsweise 1. Für p1 = p2 = p3 = p4 = p , 2. Für p1 = p2 = p3 = ½ , p4 = p , wo p und q = 1 - p von ½ verschieden seien:
1. 2.
W[a] = q4 1/8 q
W[a+i] = 4pq3 1/8 (3q+p)
W[a+2i] = 6p²q2 1/8 (3q+3p)
W[a+3i] = 4p3q 1/8 (q+3p)
W[a+4i] = p4 1/8 p
Man kann so immer wieder andere asymmetrische Verteilungsweisen als Spezialisierungen des allgemeinen Schemas (44) angeben, während nur auf obige Art eine symmetrische Verteilung möglich ist. Aber jede derselben beruht in gleicherweise auf der Hypothese, daß vier von einander unabhängige Kräfte vorhanden sind, von welchen jede eine bestimmte W. für ihr Wirksamwerden besitzt und im Falle ihres Wirkens den Größenzuwachs i erzeugt.]
[Nun gibt es allerdings in Wirklichkeit keinen K.-G., der nur fünf, durch endliche und konstante Intervalle getrennte Größenstufen unterscheiden läßt. Vielmehr verteilen sich die Exemplare stetig auf das durch die extremen Werte begrenzte Größengebiet, so daß man auch durch eine Vermehrung der Größenstufen, wo dann statt fünf eine größere Zahl zu wählen wäre, nichts gewinnt. Wohl aber laßt sich der Größenbereich, den die Exemplare des K.-G. stetig erfüllen, in Intervalle von konstanter Größe i abteilen und die Intervallgröße der Art bestimmen, daß innerhalb jedes einzelnen Intervalles die Verteilung der Exemplare als gleichmäßig und das Verteilungsgesetz als konstant angenommen werden darf. Dies ist der Fall, wenn i eine kleine Größe vorstellt, deren zweite Potenz im Vergleiche zu endlichen Größen vernachlässigt werden darf. Dann ist es auch gestattet, die auf das Intervall fallenden Exemplare in der Intervallmitte vereinigt zu denken, so daß man auf diesem Wege zu der Vorstellung der Größenstufen mit konstanten Intervallen zurückgeführt wird. Die anfängliche Vorstellungsweise ist jedoch jetzt insofern modifiziert, als die Exemplare nicht mehr den einzelnen Größenstufen selbst, sondern den zugehörigen Intervallen angehören, und die Größenstufen nur als Repräsentanten der Intervalle dienen.]
[Mit Berücksichtigung dieser Modifikation kann nun der von den Exemplaren des K.- G. erfüllte Größenbereich durch eine unbestimmt große Anzahl von Größenstufen ersetzt werden, so daß die auftretenden Größen selbst durch
a , a + i , a + 2i , .... a + ni (45)
darstellbar sind. Man hat daher nur nötig, an Stelle der im obigen Beispiele gewählten beschränkten Anzahl von vier Kräften eine unbestimmt große Anzahl n solcher Kräfte vorauszusetzen und jeder eine bestimmte W. für ihr Wirksamwerden beizumessen, um für jede Größenstufe eine wie oben zu bestimmendeW. und damit eine bestimmte Verteilung der Exemplare auf das ganze Größengebiet zu erhalten. Zugleich erhellt, daß diese Verteilung nur dann symmetrisch ist, wenn sich die n Kräfte paarweise zusammenfassen lassen und für jedes Paar, dessen W. gleich piund pkseien, pi + pk = 1 ist. Jede andere Bestimmung dieser W. führt zu einer asymmetrischen Verteilung. Soll aber die letztere in ihrer Gesetzmäßigkeit verfolgt werden können, so darf nicht regellos jeder wirkenden Kraft eine ganz willkürlich gewählte W. zuerteilt werden. Es möge darum im Interesse der Durchführbarkeit der mathematischen Behandlung jeder Kraft die nämliche W. für ihr Wirksamwerden beigemessen werden.]
[Man wird so zu folgender Hypothese geführt:
1) Es wird eine unbestimmt große Anzahl n von Kräften2)
K1 , K2, ××× Kn
2) Es besteht die W. p für das Auftreten und die W. q = 1 p für das Ausbleiben der Wirkung jeder einzelnen Kraft.3) Jede Kraft erzeugt im Falle ihres Wirkens den Zuwachs i , wo i eine so kleine Größe vorstellt, daß ihre zweite Potenz neben endlichen Größen vernachlässigt werden darf.]
2) [Die Bezeichnung "Kräfte" wird bloß der Kürze halber gewählt; es mögen darunter alle die Besonderheiten, welcher Art sie auch seien, verstanden werden, die einen ändernden Einfluß auf die Größe der Exemplare eines K.-G. auszuüben imstande sind.]
[Hiernach erhält ein Exemplar,
an dessen Erzeugung sich keine der n Kräfte beteiligt, die
Größe a , deren W. W[a] = qn,
während bei Auftreten aller Kräfte die Größe a
+ ni entsteht, für welche W[a + ni] = pnist.
Beteiligen sich aber an einem Exemplare
x Kräfte, so wird die
Größe desselben a +
xi ; und da
![]()
verschiedene Systeme von je x Kräften gebildet werden können, für jedes System aber die W.
px × qn-x
besteht, so ist:
![]() .
(46)
.
(46)
Nun gelten für große n , x und n - x die Formeln:
![]()
![]()
![]() .
.
Mit Rücksicht hierauf erhält man:
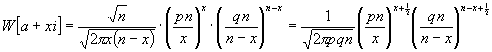 (47)
(47)
Setzt man hier pn und qn als ganze Zahlen voraus, nimmt man also an, daß n durch den gemeinsamen Nenner der Brüche p und q teilbar sei, wodurch die Allgemeinheit der folgen-den Entwicklung nicht beschränkt wird, so kann man statt x und n x mit Vorteil pn + x und qn x schreiben, wo nunmehr x alle positiven Zahlen von 0 bis + nq und alle negati-ven Zahlen von 0 bis - np zu durchlaufen hat; zugleich ist a + xi durch a + pni + xi oder, wenn a + pni kurz durch a0 bezeichnet wird, durch a0 + xi zu ersetzen. Man findet so:
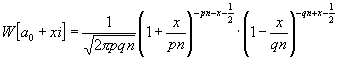 (48)
(48)
![]()
Hieraus gewinnt man mit Rücksicht, daß:
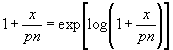 ;
; 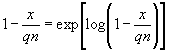
![]()
folgende Darstellungsform:
![]()
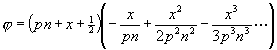
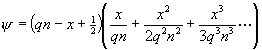 (49)
(49)
Dieselbe ist gültig, solange x : pn und x : qn kleiner als 1.]
[Soll dieses Gesetz die W. für die endlichen Werte der Abweichungen xi von a0darstellen, so muß x als Größe von der Ordnung 1 : i vorausgesetzt werden. Es ist dagegen n eine Größe höherer Ordnung, wenn die extremen Abweichungen pni und qni im Vergleich zu den in Betracht gezogenen Werten xi sehr groß sind. Dies trifft aber in der Tat zu, da die extremen Abweichungen mit der Zahl der Exemplare beiderseits wachsen und somit, vom Standpunkte der Theorie aus, als ins Unbegrenzte wachsend anzunehmen sind. Es werde darum n als eine Größe von der Ordnung 1 : i2 vorausgesetzt. Alsdann repräsentiert der Quotient x2: n eine endliche Größe und der Quotient x : n in gleicher Weise wie der Quotient x3: n2eine Größe von der Ordnung i . Man kann somit, wenn Größen von der Ordnung i² und höherer Ordnung in der Reihendarstellung von j und yvernachlässigt werden, das Wahrscheinlichkeitsgesetz (49) in folgende einfache Form bringen:
![]()
![]()
![]() ,
,
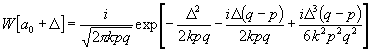 ,
(50)
,
(50)[Bei der Ableitung dieses Gesetzes wurde vorausgesetzt, daß die Exemplare des K.-G. in den Mitten a0+ xi der durch die Wertenreihe (45) repräsentierten Intervalle vereinigt gedacht werden dürfen. Es verteilen sich aber in Wirklichkeit die Exemplare stetig innerhalb der Intervalle, so daß auch die Wahrscheinlichkeitsfunktion als eine stetige Funktion der Abweichungen D anzunehmen ist, deren Integrale zwischen den Grenzen der Intervalle durch die W[a0+ D ] angegeben werden. Bezeichnet man demnach die Wahrscheinlichkeitsfunktion durch w[a0 +D] so ist:
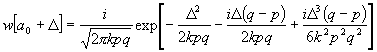 ; (51)
; (51)[Hiernach findet man durch Differentiation den Maximalwert von w aus der Gleichung:
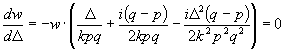 ;
;![]() .
.
Somit fällt der dichteste Wert D auf:
![]() .
.
Wird dieser Wert als Ausgangswert für das Wahrscheinlichkeitsgesetz gewählt, wird also a0 = D + ½i (q - p) ; D = ¶ - ½i (q - p) gesetzt, so resultiert schließlich, wenn w[D +¶ ] durch j (¶ ) ersetzt wird:
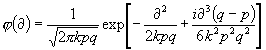
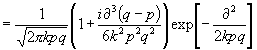 (52)
(52)
als endgültige Form des abzuleitenden Gesetzes.]
[Es handelt sich nun noch um den Nachweis, daß der Ausgangswert D auf Grund des Gesetzes (52) approximativ das Proportionalgesetz erfüllt. Zu diesem Zwecke werde:
![]()
gesetzt, so daß:
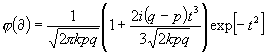 . (53)
. (53)
Nun ist, wenn m¢ die oberhalb D gelegene Anzahl und m die Gesamtzahl der Abweichungen angibt:
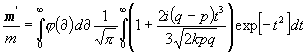
![]() .
.
Entsprechend ist für die unterhalb D gelegene Anzahl m,:
![]() .
.
Bezeichnet man ferner die oberhalb und unterhalb D gelegenen Summen der Abweichungen durch å¶' und å¶,, so wird:
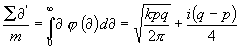
![]() .
.
Man findet hieraus:
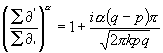 ;
; 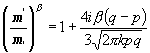 . (54)
. (54)
Somit ist:
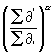 =
= ![]() ,
wenn b = ¾pa
= 2,356 a. (55)
,
wenn b = ¾pa
= 2,356 a. (55)
In erster Annäherung kann man demnach
a = 1 ; b = 2
setzen, so daß in der Tat approximativ:
![]()
![]() ,
(55a)
,
(55a)
wie das Proportionalgesetz es verlangt.]
[Gilt aber das Proportionalgesetz, so kann mit entsprechender Approximation das zweiseitige G. G. an Stelle des einheitlichen Wahrscheinlichkeitsgesetzes (52) treten. Dasselbe ist in der Form (6), welche sich auf die beiderseitigen Abweichungen bezieht, vorauszusetzen, da auch das Gesetz (52) die oberen und unteren Abweichungen zugleich berücksichtigt. Es sei also:
![]()
![]() . (56)
. (56)
Hier ist auf Grund der berechneten Abweichungszahlen und
Abweichungssummen:
![]()
![]()
![]()
![]() (56b)
(56b)
zu setzen; auch kann mit der nämlichen Berechtigung in der Darstellung von h' und h, statt ½p- 2/3ebensowohl ¼p als auch 2/3gesetzt werden.]
[Die Ersetzung des einheitlichen Gesetzes (52) durch das zweiseitige G. G. hat demnach zur Folge, daß an Stelle des Gliedes
![]()
das Glied
![]()
tritt, das für positive ¶ ein positives, für negative ¶ ein negatives Vorzeichen erhält.]
[Sowohl (52) als auch (56) stellt für
p
= q das einfache G. G. dar, das somit als Spezialfall zugleich mit
jenen allgemeinen Gesetzen aus der aufgestellten Hypothese entwickelt wird.
Wird letztere diesem Falle von vornherein angepaßt, so unterscheidet
sie sich nicht wesentlich von der Hypothese, die HAGEN3)
zur Ableitung des einfachen G. G. für die Fehlertheorie aufgestellt
hat.]
3) [Grundzüge der Wahrscheinlichkeitsrechnung, Berlin
1837. S. 34. Die Hypothese HAGEN's lautet: "Der Fehler im Resultate
einer Messung ist die algebraische Summe aus einer unendlich großen
Anzahl elementarer Fehler, die alle gleich groß sind, und von denen
jeder einzelne ebenso leicht positiv wie negativ sein kann.".]
[Beachtung verdient es, daß die Asymmetrie hier durch Größen von der Ordnung i repräsentiert wird. Sie wird daher unendlich klein, wenn i unendlich klein wird. Bei der obigen Ableitung wurde aber i nicht als unendlich klein, sondern nur als so klein vorausgesetzt, daß i2gegen endliche Größen vernachlässigt werden darf.]
[Noch ist zu erwähnen, daß für das einheitliche Wahrscheinlichkeitsgesetz an Stelle des dichtesten Wertes D ebensowohl ein anderer Wert als Ausgangswert gewählt werden kann. In der Darstellungsform (51) ist es beispielsweise der arithmetische Mittelwert, der zum Ausgangspunkt der Abweichungen gemacht ist. Man findet nämlich bezüglich a0die Summen der beiderseitigen Abweichungen einander gleich, so daß a0in der Tat das arithmetische Mittel A darstellt.]