§ 123. Bisher ist das G. G., soviel mir bekannt, bloß zur Bestimmung der verhältnismäßigen oder absoluten Zahl der Abweichungen D von A zwischen gegebenen Grenzen der Abweichung benutzt worden; aber es lassen sich in Zusammenhang damit und gewissermaßen als Korollar davon auch Formeln für die verhältnismäßige und absolute Summe der Abweichungen von A zwischen gegebenen Grenzen der Abweichung entwickeln, welche, wie die Formeln bez. des G. G. überhaupt, so lange gültig und für die beiderseitigen Abweichungen gemeinsam anwendbar bleiben, als eine symmetrische W. der Abweichungen bez. A besteht; im Falle der asymmetrischen W. aber wiederum nach dem zweispaltigen G. G. ihre Gültigkeit für jede Seite insbesondere in Anspruch nehmen, wenn man die Abweichungen bez. D statt bez. A nimmt, und m , åD , h, t für jede Seite insbesondere respektiv durch m,, å¶,, e,, t,und m' , å¶' , e' , t' ersetzt.
Es verdienen aber die Ergebnisse in Bezug auf die Summe der Abweichungen um so mehr Beachtung, als sie den Nachteil der Ergebnisse bezüglich der Zahl der Abweichungen nicht teilen, nur durch ein auf einen endlichen Ausdruck nicht zurückführbares Integral oder eine unendliche Reihe, hiernach tabellarisch dargestellt werden zu können, da sie vielmehr in endlicher Form ausdrückbar sind, außerdem durch das Supplementarverfahren (§128), das sie ermöglichen, wichtig werden, Es gilt nämlich nach dem unten auseinander zu setzenden Gange folgendes.
§ 124. Um die Summe der Abweichungen
bis zu einer gewissen Abweichungsgrenze vom dichtesten Werte aus nach einer
Seite, sagen wir der positiven, also bis zur Grenze ¶'
,
zu bestimmen, wovon das Entsprechende für die negative Seite gilt,
nehme man die Totalsumme der Abweichungen nach dieser Seite, d. i.
å¶'
, bilde hieraus die einfache mittlere Abweichung e' = å¶
' : m' , nehme t =
¶
' : e'![]() ,
bilde daraus nach unten folgender Regel den Wert exp [ - t2],
dann ist die absolute Summe der Abweichungen von ¶'
= 0 bis zum gegebenen ¶' gleich:
å¶'(1
- exp [ - t²]) und die darüber hinaus von ¶'
bis
¥ liegende gleich: å¶'×exp[
-t²]; die verhältnismäßige Summe bis
¶'
aber, d. i. die vorige absolute, dividiert durch die Gesamtsumme å¶'
,
welche mit T bezeichnet werde, gleich 1 - exp [ - t2],
darüber hinaus exp [ - t2].
,
bilde daraus nach unten folgender Regel den Wert exp [ - t2],
dann ist die absolute Summe der Abweichungen von ¶'
= 0 bis zum gegebenen ¶' gleich:
å¶'(1
- exp [ - t²]) und die darüber hinaus von ¶'
bis
¥ liegende gleich: å¶'×exp[
-t²]; die verhältnismäßige Summe bis
¶'
aber, d. i. die vorige absolute, dividiert durch die Gesamtsumme å¶'
,
welche mit T bezeichnet werde, gleich 1 - exp [ - t2],
darüber hinaus exp [ - t2].
Anstatt die absolute und verhältnismäßige Summe bis zu einer gewissen Grenze ¶' und darüber hinaus zu bestimmen, kann man diese Bestimmung auch bis zu einer gewissen Zahl der Abweichungen, welche z' heiße, vornehmen, sofern bei großem m' , wie es hier vorausgesetzt ist, z¢: m' nach dem in voriger Weise bestimmten t und umgekehrt als F in der t - Tabelle gefunden werden kann. Sei also z' :m¢ gegeben, so suche man in der t - Tabelle das t und verwende es in voriger Weise zur Summenbestimmung.
Insofern jeder Wert a in der a - Spalte der Verteilungstafel eigentlich ein ganzes Intervall i repräsentiert, in welchem sich die auf a geschriebenen z - Werte verteilen, was wir das Umkreisintervall des betreffenden a nennen, so ist die Grenze, bis zu welcher wir die Summe wie Zahl der Abweichungen zu nehmen haben, nicht durch ein a der a - Spalte selbst, sondern durch die Grenze von dessen Umkreisintervall, wodurch es sich an das Umkreisintervall des benachbarten a anschließt, als bestimmt anzusehen.
Anstatt die Summe bis zu gegebenen Grenzen von D aus jederseits zu bestimmen, kann man sie auch zwischen beliebigen Grenzen jederseits ganz in derselben Weise als die Zahl jederseits bestimmen, indem man die den Grenzen nach ersterer Bestimmungsweise zugehörigen Summen von einander abzieht.
§ 125. Um exp [ - t2] zu finden, addiere 2 log t zu 0,63778 - 1, suche hierzu die Zahl in den Logarithmentafeln, nimm sie negativ, d. h. ziehe sie von der nächst größeren ganzen Zahl ab und füge diese hinten mit negativem Vorzeichen hinzu; hierzu suche wieder die Zahl, so ist dies exp [ - t2].
Diese Berechnung hat an sich natürlich
keine Schwierigkeit, ist aber, wie man sieht, etwas umständlich, und
um sie für die einzelnen Fälle zu ersparen, kann man dann allerdings
für äquidistante t =D : h![]() oder, um die Multiplikation von h mit
oder, um die Multiplikation von h mit ![]() zu ersparen, für solche von D :h
die zugehörigen Werte von
zu ersparen, für solche von D :h
die zugehörigen Werte von
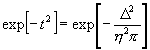
und hiernach 1 - exp [ - t2]
angeben und die äquidistanten Werte einander nahe genug nehmen, um
dann dazwischen zu interpolieren. Hier folgt eine solche Tabelle, deren
Werte freilich noch einander näher liegen müßten, um eine
sehr genaue Interpolation zu gestatten.
Tabelle über die Abweichungssummen von D
bis ¥ , die Totalsummme als Einheitgesetzt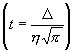 ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
||||
|
|
|
§ 126. Die Ableitung des Summengesetzes in Abhängigkeit von A nach einfachem G. G. ist diese.
Nach dem einfachen G. G. ist die beiderseits
zusammengenommene absolute Zahl der Abweichungen zwischen t = 0
und einem gegebenen Werte von t = D :
h![]() :
:
 ;
kurz mF [t]. (1)
;
kurz mF [t]. (1)
Um die zugehörige Summe zu haben, hat man vorigen Wert unter dem Integralzeichen mit D zu multiplizieren, was gibt:
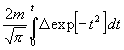 .
(2)
.
(2)
Da aber t = D:
h![]() mithin D = th
mithin D = th![]() , so hat man durch Substitution dieses Wertes für Din
voriges Integral:
, so hat man durch Substitution dieses Wertes für Din
voriges Integral:
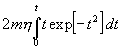 .
(3)
.
(3)
Das allgemeine Integral von 2 òt
exp[ - t²] dt ist mit Rücksicht, daß tdt
= d ![]() t2,
in endlicher Form integrierbar, nämlich gleich - exp[ -t2]
und mithin zwischen den Grenzen t = 0 und t = t gleich (1
- exp [ - t2]), was mit mh
= åD
multipliziert, gibt:
t2,
in endlicher Form integrierbar, nämlich gleich - exp[ -t2]
und mithin zwischen den Grenzen t = 0 und t = t gleich (1
- exp [ - t2]), was mit mh
= åD
multipliziert, gibt:
åD (1 – exp [ - t²]) , (4)
Sei kurz
Nun ist in unendlicher Reihe ausgedrückt:
§ 127. Um Beobachtung mit Rechnung zu vergleichen, gilt es natürlich, die Abweichungssumme selbst bis zu gegebenen Grenzen zu bestimmen. Nun gilt für die empirische Bestimmung der totalen å¶ jeder Seite (nach § 74):
å¶' = åa' - m¢D ; (9)
Erläutern wir dies an der Tafel I der 450 Schädel. [Für die Reduktionslage E,= 368 (§ 64) fällt Dp = 409,7 in das Intervall 405,5 – 410,5. Es ist somit a0 = 408; z0 = 65; i = 5; g1 = 405,5; x = 4,2 , und man erhält für das von Dpbis zur ersten Intervallgrenze 405,5 reichende å¶" , d. i. für y Dp – Y , wo y die Zahl und Y die Summe des Eingriffsintervalles angibt, nach den Formeln (13) und (8) des IX. Kapitels:
Vergleich der empirischen å¶" mit den theoretischen für Tafel I (Vertikalumfang des Schädels).
E = 1 mm; i = 5; Dp = 409,7; e,= 11,9; å¶,= 2840.
|
|
|
|
|
|
||
| empir. |
|
empir. | Theor. | |||
| 0 bis 4,2 | 116 | 111 | - 5 | 0,041 | 0,039 | - 0,002 |
| " 9,2 | 511 | 491 | - 20 | 0,180 | 0,173 | - 0,007 |
| " 14,2 | 991 | 1034 | +43 | 0,349 | 0,364 | + 0,015 |
| " 19,2 | 1592 | 1599 | + 7 | 0,561 | 0,563 | + 0,002 |
| " 24,2 | 2113 | 2079 | - 34 | 0,744 | 0,732 | - 0,012 |
| " 29,2 | 2566 | 2423 | - 143 | 0,904 | 0,853 | - 0,051 |
| " 34,2 | 2725 | 2636 | - 89 | 0,960 | 0,928 | - 0,032 |
| " 39,2 | 2798 | 2749 | - 50 | 0,982 | 0,968 | - 0,014 |
| " 44,2 | 2840 | 2806 | - 34 | 1,000 | 0,988 | - 0,012 |
Hieraus ist zu ersehen, mit welcher Annäherung die absoluten und relativen Abweichungssummen, wie sie die Tafel hergibt, durch das Summengesetz dargestellt werden. Dabei ist in Rücksicht zu ziehen, daß die empirischen Werte unter der Voraussetzung einer gleichmäßigen Verteilung der a resp. ¶ innerhalb der einzelnen Intervalle bestimmt wurden, während der theoretischen Berechnung die Annahme zu Grunde liegt, daß die Verteilung auch innerhalb der Intervalle dem G. G. entspreche.]
§ 128. Zusatz. Das Supplementarverfahren.
Wenn, wie allgemein üblich, in einer Verteilungstafel bloß die Gesamtzahl, aber nicht die Gesamtsumme der a , welche über und unter einen gewissen Wert fallen, kurz bloß die Vorzahl v und Nachzahl n , aber nicht die Vorsumme V und Nachsumme N gegeben ist, so läßt sich zwar C , aber weder A noch Dpdirekt erhalten, ebensowenig die Abweichungsfunktionen bezüglich dieser Werte, also wird auch keine Verteilungsrechnung möglich sein. Inzwischen kann man dazu nach folgendem, freilich etwas mühsamem, Verfahren, welches ich das Supplementarverfahren nenne, gelangen.
Man bestimmt statt Dpvielmehr Di , welches in der Regel von Dp so wenig abweicht, um dafür substituiert werden zu können, läßt zunächst eine Rücksicht auf v , V , n , N bei Seite, sondern bestimmt die noch unvollständigen Abweichungszahlen m" , m" und Abweichungssummen å¶" , å¶" nach bekannter scharfer Methode bloß aus dem ausgeführten Teile der Tafel. Man bestimmt aber auch die totalen Abweichungszahlen m,= m" + v und m' = m" + n , hiernach v : m,und n : m' . Diesen Werten zugehörig kann man in folgender Tabelle Werte afinden, deren Berechnungsweise nachher angegeben wird, durch die Tabelle aber soll, wenigstens für einige Werte, die Mühe der Berechnung erspart werden. Die Tabelle ist bloß auf kleine Werte v : m,und n : m¢ ausgedehnt, da es sich in weit den meisten Fällen nur um solche handelt; wo die Tabelle nicht ausreicht, muß adirekt berechnet werden.
Hiernach findet man die volle Summe der unteren und oberen Abweichungen von Di wie folgt:
![]() ,
, ![]() .
(10)
.
(10)
Hiernach1):
![]() ,
, ![]() ;
;
![]() .
(11)
.
(11)
1) [Da die hierbei vorauszusetzende Gültigkeit des zweispaltigen
G. G. bezüglich Di das Bestehen des Proportionalgesetzes:
e'
: e,= m'
: m,zur
Folge hat, so kann mit Rücksicht darauf statt der obigen, ohne Berücksichtigung
dieses Gesetzes geltenden Formel auch direkt: A = Di + e'
- e, gesetzt werden, was verglichen
mit der obigen Ableitung von A einen Anhalt für die Sicherheit
der Bestimmung gewährt.]
Einige zu den Zahlenwerten v : m,, n : m' zugehörige Summenbruchwerte ader Abweichungen jeder Seite bezüglich D.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Die Berechnung von a geschieht so: Man suche zu m":m,, oder zu m": m' , je nachdem es sich um die negative oder positive Seite handelt, als F[t] genommen, den Wert t und nehme a = exp [ - t²] .
Diese Bestimmungsweise ist davon abhängig, daß man für jede Seite der Abweichungen von Diaus das einfache G. G. nach der insbesondere für diese Seite gefundenen Zahl und mittleren Abweichung für gültig hält, kurz das modifizierte G. G. für die Totalität statuiert, und hängt an dem in folgender Einschaltung entwickelten Prinzip.
[Die drei Werte: 1) die relative Zahl der Abweichungen, 2) die relative Summe der Abweichungen, 3) der Quotient aus der Abweichung selbst, bis zu welcher von Di aus die relative Zahl und Summe bestimmt werden, und aus der mittleren Abweichung, stehen in solcher Abhängigkeit von einander, daß je zwei aus dem dritten berechnet werden können. Es ist nämlich auf Grund des G. G. für die Abweichungen einer Seite, beispielsweise der positiven:
![]() ;
; ![]() ;
; ![]() ;
(12)
;
(12)
wo m' und å¶' die gesamte Zahl und Summe der Abweichungen dieser Seite vorstellen, ¶" aber die Abweichung bedeutet, bis zu welcher die unvollständige Zahl m" und die unvollständige Summe å¶'' erstreckt werden. Es kann daher, in der oben angegebenen Weise, zu m" : m' resp. m":m,durch Vermittlung von t der Wert å¶'': å¶ ' resp. å¶": å¶, berechnet und hieraus, wenn å¶" resp. å¶"empirisch gefunden ist, å¶' resp. å¶, nach (10) bestimmt werden.]
Um diese Bestimmung an einem speziellen
Beispiele zu erläutern, so ist in QUETELET's Tafel der französischen
Rekruten2) v = 28 620 ; n
= 2490 ; m = 100 000 . [Man findet nun Di=
1,6273 m, also m,=
55 951 ; m' = 44 049 ; m":m,=
0,48848 ; m": m'
= 0,94347 ; hiernach aus der t - Tabelle erstenfalls t =
0,46420 und 1 - exp [ - t2] =
0,19385 ; zweitenfalls t = 1,34843 und 1 - exp [ - t2]
= 0,83769 . Folglich erhält man aus (10) die Totalsumme å¶,
=
3740,5 ; å¶' = 2410,7 , da
å¶"=
725,1 und å¶" = 2019,4 . Schließlich
ergibt sich auf Grund von (11) e,=
0,0669 ; e' = 0,0547 ; A = 1,6140 . Es ist somit D - A
= 0,0133, während e,- e'
= 0,0122 ; beide Werte sollten einander gleich sein, ihr Auseinanderweichen
aber hat darin seinen Grund, daß der Ausgangswert Divon
dem proportional bestimmten Dp
etwas abweicht. QUETELET selbst, der durch abschätzende Vergleichung
der beobachteten Wahrscheinlichkeitswerte mit den theoretischen Werten
seiner Wahrscheinlichkeitstafel zur Aufstellung einer durchgeführten
Verteilungstafel gelangt, sagt: "la taille moyenne est de 1,62 m environ".]
2 ) [Lettres sur la théorie des
probabilités, p. 401. "Taille des conscrits francais".]
Man könnte nun meinen, daß auch in Fällen, wo eine vollständige Reihe vorliegt, die beobachteten Werte aber nach unten abnorm zu klein werden, wie es bei den Leipziger und Annaberger Rekrutenmaßen der Fall ist, man nur das Supplementarverfahren auf den höheren Teil der Reihe, der aber noch auf derselben Seite von D liegt, anzuwenden brauche, um ein å¶,zu erhalten, was am Einflüsse der Abnormität nach unten unbeteiligt oder so beschaffen ist, als wenn das normale Verhältnis zwischen Zahl und Größe der Abweichungen, was man nach oben voraussetzt, auch bis zum unteren Ende reichte. Aber dies ist nicht der Fall, vielmehr kann man vom Supplementarverfahren nur insoweit ein brauchbares Ergebnis erwarten, als der bei der Berechnung ausgeschlossene untere Teil der Reihe, welcher b heiße, ebenso normal ist, als der bei der Berechnung zugezogene , welcher a heiße. In der Tat nehmen wir an, die verhältnismäßige Zahl der Abweichungen von einem gewissen Abweichungswerte bis zum Ende, d. i. im Teile b , sei zu groß, so wird die verhältnismäßige Zahl darüber, im Teile a , abnorm zu klein sein; beim Supplementarverfahren aber setzt man voraus, daß sie normal sei, was sich widerspricht. Daher kommt man auch, wenn man doch nach dem Supplementarverfahren bei solch abnormen Reihen verfährt, zu absurden Folgerungen. Natürlich vermindert sich in solchen Reihen durch das Supplementarverfahren der direkt erhaltene Wert å¶,, und steigt der Wert von A . — So habe ich bei den Leipzigern als a nach negativer Seite den Teil genommen, der von D = 69,71 bis 66,5 reicht, als b den Teil von da bis zu Ende, wobei man sich (nach § 15) erinnern kann, daß 66 der Wert ist, unterhalb dessen die Untermäßigen fallen. Der aus der Totalität abgeleitete Wert von å¶, war 9935 , der nach dem Supplementarverfahren abgeleitete 9097, merklich gleich mit dem Werte von å¶' = 9070 , welcher aus dem als normal angesehenen positiven Teile der Reihe folgt. Der aus der Totalität der Reihe direkt abgeleitete Wert von A war 69,62 , der nach dem Supplementarverfahren gewonnene 69,70 , also dem Werte D merklich gleich. Wäre nun aber D wirklich der Mittelwert, so müßte auch der Zentralwert damit zusammenfallen, also m' = m,sein, wogegen m,= 4257 ; m' = 4145 ist.