Es ist schon angeführt, daß
die bis jetzt vorliegenden, ausgeführten Verteilungstafeln des G.
G., d. i. die F -Tafel und j
-Tafel, nicht bez. D : h,
wofür sie § 27 gegeben wurden, sondern bez. D:
h![]() ,
kurz t , aufgestellt sind. Eine solche Tafel wird im Anhang (§
183) mitgeteilt.
,
kurz t , aufgestellt sind. Eine solche Tafel wird im Anhang (§
183) mitgeteilt.
Derselben liegt die fundamentale GAUSS'sche Bestimmung unter, daß die W. oder verhältnismäßige Zahl eines einzelnen Wertes ± D kurz eine bestimmte Größe sei, gleich:
![]() , (1)
, (1)
worin ![]() ,
, ![]() .
.
Um sie zwischen gegebenen Grenzen von D zu haben, hat man vorigen Ausdruck mit dDzu multiplizieren und das Integral davon zwischen den betreffenden Grenzen zu nehmen; gibt allgemein:
![]() (2)
(2)
oder nach Ersatz von h durch 1 : h![]() , D durch h
, D durch h![]() t
, dD durch h
t
, dD durch h![]() dt
:
dt
:
![]() (3)
(3)
und die W. oder verhältnismäßige Zahl
der D zwischen t = D:h![]() =
0 und einem gegebenen t ist hiernach:
=
0 und einem gegebenen t ist hiernach:
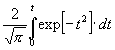 , kurz = F [t] . (4)
, kurz = F [t] . (4)
Diese Wahrscheinlichkeit F [t] wird nun eben für die verschiedenen Werte t durch die im Anhang gegebene Tabelle ausgedrückt. Um die absolute Zahl der D zwischen den Grenzen t = 0 und einem gegebenen t zu haben, hat man F [t] noch mit der Totalzahl m zu multiplizieren.
Der Integralausdruck für F
[t] läßt sich bekanntlich nicht in endlicher Form integrieren,
wohl aber in folgender unendlichen Reihe darstellen, welche so lange stark
konvergiert und mithin zur Berechnung von F
brauchbar
ist, als t = D : h![]() kleiner als 1 , mithin D < h
kleiner als 1 , mithin D < h![]() ,
d. i. < 1,772 45 × h
ist:
,
d. i. < 1,772 45 × h
ist:
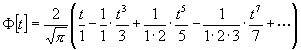 (5)
(5)
Da die F folgends immer bez.
t
genommen sind, kann die Zufügung [t] übergangen werden.
Alle Potenzen von t sind positiv, weil t = D
: h![]() ,
D
und h aber zugleich positiv und negativ werden.
,
D
und h aber zugleich positiv und negativ werden.
Nun ist wichtig zu bemerken, daß,
wenn, wie vielfach bei unseren Anwendungen der Fall, der Wert D
, welcher in t = D : h![]() eingeht, sehr klein gegen den Mittelfehler h,
mithin t selbst sehr klein ist, alle Glieder der Reihe (5) gegen
das erste vernachlässigt werden können; wonach approximativ:
eingeht, sehr klein gegen den Mittelfehler h,
mithin t selbst sehr klein ist, alle Glieder der Reihe (5) gegen
das erste vernachlässigt werden können; wonach approximativ:
![]() (6)
(6)
![]() . (7)
. (7)
Doch wird bei dieser Vernachlässigung der höheren Glieder nach Ansicht von (5) der Wert F um eine Kleinigkeit zu groß bestimmt, und haben wir also genauer zu setzen:
![]() ,
(8)
,
(8)
wo w ein sehr kleiner positiver Wert ist. Aus (8) aber folgt:
![]() , (9)
, (9)
wonach t bei Vernachlässigung von w, d. i. nach dem approximativen Werte (7), etwas zu klein gefunden wird.
§ 119. Der Wert h hat nach dem G. G. bestimmte Normalbeziehungen zu manchen anderen, aus den Verteilungstafeln ableitbaren Werten, insofern sie dem G. G. unterliegen, deren Bestätigung um so approximativer zu erwarten ist, je mehr m wächst.
Sei q = ![]() die
Wurzel aus dem mittleren Abweichungsquadrat, welche bei den Astronomen
als mittlere Abweichung schlechthin gilt, und w die sogenannte wahrscheinliche
Abweichung, d.i. die Abweichung, die, wenn man positive und negative Abweichungen
beide nach absolutem Werte nimmt, eben so viele größere Abweichungen
über sich als kleinere unter sich hat, also im Grunde der Zentralwert
der Abweichungen, nicht zu verwechseln mit unserem Zentralwerte schlechthin,
der mit C bezeichnet wird, indem dieser nicht eine Abweichung D
, sondern ein a ist. Man hat nun folgende Normalbeziehungen:
die
Wurzel aus dem mittleren Abweichungsquadrat, welche bei den Astronomen
als mittlere Abweichung schlechthin gilt, und w die sogenannte wahrscheinliche
Abweichung, d.i. die Abweichung, die, wenn man positive und negative Abweichungen
beide nach absolutem Werte nimmt, eben so viele größere Abweichungen
über sich als kleinere unter sich hat, also im Grunde der Zentralwert
der Abweichungen, nicht zu verwechseln mit unserem Zentralwerte schlechthin,
der mit C bezeichnet wird, indem dieser nicht eine Abweichung D
, sondern ein a ist. Man hat nun folgende Normalbeziehungen:
![]() =
1,253 314 × h,
also merklich = 5/4h;
=
1,253 314 × h,
also merklich = 5/4h;
![]() =
0,797 885 × q , also merklich
=
4/5 q
;
(10)
=
0,797 885 × q , also merklich
=
4/5 q
;
(10)
q = 1,482 604 ×w ; w = 0,674 489 × q
h = 1,182 947 ×w ; w = 0,845 347 × h
Durch Substitution der vorigen Ausdrücke für
h
in t = D : h![]() kann
man also auch ohne Änderung des zugehörigen Fsetzen:
kann
man also auch ohne Änderung des zugehörigen Fsetzen:
![]() oder t =
oder t = ![]() , (11)
, (11)
Hiernach erscheint es zunächst
gleichgültig, an welchen Ausdruck für t man sich hält.
Nur ist es nicht ganz gleichgültig, ob man zunächst q aus
den Quadraten der Abweichungen, åD2,
bestimmt, um danach hoder w mittelst
der vorigen Formeln zu finden, oder umgekehrt hoder
w aus den einfachen Abweichungen, um aus einem dieser Werte die anderen
zu finden, sondern die direkte Bestimmung von q aus den Quadraten
der Abweichungen hat eine etwas größere Sicherheit, als die
von hals Mittel der einfachen Abweichungen,
und letztere eine nicht unerheblich größere, als die von w
durch
Abzählen der Abweichungen, was sich auf die nach obigen Formeln daraus
abgeleiteten Werte überträgt. Daher hält man sich in der
physikalischen und astronomischen Maßlehre am liebsten an den Wert
t = D : q![]() ,
nach direkter Bestimmung von q aus den Quadraten der Abweichungen;
gewönne aber auch dieselbe Sicherheit durch Anwendung der anderen
Ausdrücke für t , wenn man h oder
w
darin nach obigen Formeln aus dem direkt bestimmten q abgeleitet
hat, wogegen die Sicherheit geringer ist, wenn man hoder
gar w im Ausdruck von t direkt aus den einfachen Abweichungen
bestimmt, und man gewinnt nichts durch Anwendung des Ausdruckes t =D
: q
,
nach direkter Bestimmung von q aus den Quadraten der Abweichungen;
gewönne aber auch dieselbe Sicherheit durch Anwendung der anderen
Ausdrücke für t , wenn man h oder
w
darin nach obigen Formeln aus dem direkt bestimmten q abgeleitet
hat, wogegen die Sicherheit geringer ist, wenn man hoder
gar w im Ausdruck von t direkt aus den einfachen Abweichungen
bestimmt, und man gewinnt nichts durch Anwendung des Ausdruckes t =D
: q![]() ,
wenn q darin durch Anwendung voriger Formeln aus dem direkt bestimmten
h
oder w abgeleitet ist.
,
wenn q darin durch Anwendung voriger Formeln aus dem direkt bestimmten
h
oder w abgeleitet ist.
Obschon nun nach Vorigem die Benutzung
des Wertes t = D : q![]() ,
nach direkter Bestimmung von q , einen prinzipiellen Vorteil
der Sicherheit vor den anderen Bestimmungsweisen von t voraus hat,
wird man sich doch in der Kollektivmaßlehre im allgemeinen lieber
des Wertes t = D : h
,
nach direkter Bestimmung von q , einen prinzipiellen Vorteil
der Sicherheit vor den anderen Bestimmungsweisen von t voraus hat,
wird man sich doch in der Kollektivmaßlehre im allgemeinen lieber
des Wertes t = D : h![]() nach
direkter Bestimmung von h aus åD
bedienen, weil bei der großen Menge der Abweichungen, mit welchen
man im allgemeinen in dieser Maßlehre zu tun hat, die Quadrierung
derselben zu umständlich sein würde, der Vorteil der Sicherheit
bei Anwendung des direkt bestimmten q vor der des direkt bestimmten
h
doch nur unbedeutend ist, und bei großem
m überhaupt
seine Bedeutung merklich verliert. In der Tat, während der wahrscheinliche
Fehler des direkt bestimmten q gleich
nach
direkter Bestimmung von h aus åD
bedienen, weil bei der großen Menge der Abweichungen, mit welchen
man im allgemeinen in dieser Maßlehre zu tun hat, die Quadrierung
derselben zu umständlich sein würde, der Vorteil der Sicherheit
bei Anwendung des direkt bestimmten q vor der des direkt bestimmten
h
doch nur unbedeutend ist, und bei großem
m überhaupt
seine Bedeutung merklich verliert. In der Tat, während der wahrscheinliche
Fehler des direkt bestimmten q gleich
![]()
ist, ist der des direkt bestimmten h gleich und der des
![]()
direkt bestimmten w gleich
![]() 1)
.
1)
.
1) [Die Ableitung
dieser wahrscheinlichen Fehler gibt GAUSS in der Zeitschrift für Astronomie
Bd. I (Werke; Bd. IV; S. 116, 117) und encke in der Abhandlung über
die Methode der kleinsten Quadrate (Berliner Astron. Jahrbuch für
1834 S. 293 und 298). Es ist zu beachten, daß der Zahlenwert für
w
, der sich an der angegebenen Stelle bei GAUSS findet, entstellt ist.]
§ 120. Alles Vorige sind bekannte Dinge. Es mag aber nicht ohne Interesse sein, hierzu noch einige, von mir selbst aus dem G. G. abgeleitete Sätze zu fügen.
Man muß sich hüten, die Summe der Abweichungsquadrate åD 2 mit dem Quadrate der Abweichungssumme (åD )2 zu verwechseln. Wenn man sich nun die Mühe gibt, außer dem letzteren, einfach durch Quadrierung von åD zu gewinnenden Werte auch ersteren mühseliger durch Bestimmung der Abweichungsquadrate zu erhalten, so kann man mit Rücksicht, daß (åD )2 = (mh)2 und åD 2= mq2 ,aus der Gleichung:
![]()
leicht die interessante Gleichung:
![]() , (12)
, (12)
oder, wenn man den Ausdruck auf linker Seite P nennt,
ableiten, wonach die mit 2m , d. i. der doppelten Abweichungszahl multiplizierte Summe der Abweichungsquadrate, dividiert durch das Quadrat der Abweichungssumme, gleich dem Kreisverhältnisse p ist. Kurz mag die Formel die P-Formel heißen.
Andererseits erhält man nach voriger Formel die direkt mühsam zu berechnende Summe der Abweichungsquadrate aus dem leichter zu bestimmenden Quadrate der Abweichungssumme nach der Formel:
![]() , (13)
, (13)
nur daß die direkt bestimmte Summe åD2 etwas sicherer bestimmt ist als die nach voriger Formel aus (åD )2 abgeleitete.
Zu den beiden Mittelfehlern, dem einfachen
h
= åD :m und quadratischen ![]() ,
läßt sich noch ein dritter
,
läßt sich noch ein dritter
![]() (14)
(14)
fügen, den ich den Kreismittelfehler nennen will, und der gemäß obigen Ausdruckes dadurch erhalten wird, daß man die Summe der Abweichungsquadrate mit der Summe der Abweichungen oder, was auf dasselbe herauskommt, das Quadrat des quadratischen Mittelfehlers mit dem einfachen Mittelfehler dividiert.
Ich gebe ihm obigen Namen, weil er
in Bezug auf das durch die P-Gleichung ausgedrückte Kreisverhältnis
peinen
Wendepunkt in folgendem Sinne darstellt. Setzen wir zuerst, die Gleichung
sei genau durch die vorhandenen Abweichungen erfüllt, so wird in dem
Falle, daß Abweichungen, welche größer als hp
sind, wachsen, P größer als p;
hingegen wird P kleiner als p, wenn Abweichungen,
die kleiner als hp sind, wachsen. Die Änderung
ist dem Abstande der betreffenden Abweichung von hpproportional.
Den Beweis hiervon übergehe ich 2).
2) [Er folgt daraus, daß P in seiner Abhängigkeit
von einem beliebigen einzelnen Abweichungswerte Di
,
sein Minimum erreicht, wenn ![]() oder = hp.. Zugleich erhellt, daß
P
sein absolutes Minimum mit dem Werte 2 erreicht, wenn jedes der
Di
= hp
wird.]
oder = hp.. Zugleich erhellt, daß
P
sein absolutes Minimum mit dem Werte 2 erreicht, wenn jedes der
Di
= hp
wird.]
Ich habe die P-Gleichung an vielzahligen reinen Fehlern nach der psychophysischen Methode der mittleren Fehler vortrefflich bewährt gefunden.
Nach den gegebenen Ausdrücken haben die drei Mittelfehler folgendes Verhältnis:
![]() , (15)
, (15)
und es läßt sich zeigen, daß die Abweichungssummen oberhalb dieser Mittelfehler zur Totalsumme der Abweichungen nach Kap. XVIII folgende Verhältnisse haben, wo e wie immer die Grundzahl der natürlichen Logarithmen bedeutet:
Das entsprechende Verhältnis der unteren Abweichungssummen wird natürlich durch Abzug voriger Zahlen von 1 erhalten, und es zeigt sich dann, daß die untere und obere Abweichungssumme sich bez. q sehr nahe wie 2 : 3 verhält.
Bezüglich w ist das betreffende Verhältnis der oberen Abweichungssumme 0,79655 ; der Wert aber, bezüglich dessen die obere Abweichungssumme gleich der unteren ist, ist 1,17741 ×q .
Die oberen Abweichungszahlen haben zur Totalzahl der Abweichungen folgende Verhältnisse:
0,42494 bez. h; 0,31731 bez. q ; 0,21009 bez. hp; 0,5 bez. w ;
wonach diese Verhältnisse für w , h, q , hp sehr nahe mit 5: 4 : 3 : 2 stimmen.
Noch kann man als eine mittlere Abweichung zweiter Ordnung das mit h2zu bezeichnende Mittel aus den Differenzen der einzelnen D vom Mittel h derselben definieren, d. i. [wenn åD" die Summe und m" die Anzahl der D , welche kleiner als h sind, entsprechend åD" und µ" die Summe und Anzahl der D , welche größer als h, bezeichnen, so daß µ"h - åD" = åD" - µ''h = ½ mh 2]:
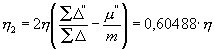 , (16)
, (16)
approximativ mit
![]()
So wie man den Wert p
durch
eine Funktion der Abweichungen nach G. G. darstellen kann, so auch den
Wert e . Sofern nämlich nach obiger Angabe die Abweichungssumme
oberhalb q dividiert durch die totale Abweichungssumme gleich ![]() ist, ist umgekehrt die totale Abweichungssumme dividiert durch die obere
bez. q und der Quotient quadriert gleich e .
ist, ist umgekehrt die totale Abweichungssumme dividiert durch die obere
bez. q und der Quotient quadriert gleich e .
§ 121. Alle vorigen Sätze
über das G. G. setzen zu ihrer vollen Gültigkeit eine große,
streng genommen unendliche Zahl der Abweichungen voraus, aus denen die
betreffenden Größen abgeleitet werden, was doch, wie schon früher
bemerkt, nicht hindert, daß schon bei einer sehr mäßigen
Zahl von Abweichungen eine sehr angenäherte empirische Bestätigung
der vorigen Sätze zu finden sei; und da zur erfolgreichen Behandlung
eines K.-G. jedenfalls eine nicht unbeträchtliche Zahl m von
Exemplaren a und mithin Abweichungen desselben nach beiden Seiten
von D gehört, so kann man nicht nur [nach Ersatz des einfachen
G. G. durch das zweispaltige] eine sehr angenäherte Bestätigung
der bisherigen Sätze dadurch erwarten, sondern auch finden. Inzwischen
verdienen die Abweichungen von den sog. wahren Werten, d. h. welche aus
einem unendlichen m folgen, oder sog. Fehler, welche je nach der
Größe des endlichen m nach beiden Seiten und des m'
und
m,nach
jeder Seite insbesondere noch übrig bleiben, immerhin wesentliche
Beachtung; und es beziehen sich darauf teils die sog. wahrscheinlichen
Fehler, teils die Korrektionen der Bestimmung aus endlichem m ,
je nachdem die Fehler den wahren Wert gleichgültig und zufällig
ins Positive oder Negative ändern oder in bestimmter Richtung um einen
von der Größe des m abhängigen Wert sei es vergrößern
oder verkleinern 3).
3 ) [Die Korrektionen für die mittleren Abweichungswerte
wurden in § 44 u. 45 mitgeteilt; die wahrschein-lichen Fehler für
h
, q und w finden sich oben § 119 angegeben. Erwähnenswert
ist auch der wahrscheinliche Fehler, der bei Bestimmung des arithmetischen
Mittels A aus m Werten zu erwarten ist, und der gleich w
:![]() zu setzen
ist, wenn w , wie üblich, den wahrscheinlichen Fehler d.i.
die wahrscheinliche Abweichung der Einzelwerte (s. oben unter (10)) vorstellt.
zu setzen
ist, wenn w , wie üblich, den wahrscheinlichen Fehler d.i.
die wahrscheinliche Abweichung der Einzelwerte (s. oben unter (10)) vorstellt.
§ 122. [Um nun die Triftigkeit des zweiseitigen G. G. im Vergleich mit dem bisher allein als Verteilungsgesetz der K.-G. in Anspruch genommenen einfachen G. G. zu erproben, sollen auf Grund der Tafeln I und III des VIII. Kapitels Vergleichstabellen zwischen den beobachteten und berechneten z-Werten hergestellt werden. Es eignen sich jene Tafeln zu einem solchen Vergleiche, da sie eine bloß schwache Asymmetrie besitzen und somit zu der Erwartung berechtigen, daß ein durch die Anwendung des zweiseitigen Gesetzes gebotener Vorteil bei stärkerer Asymmetrie sich in verstärktem Maße wiederfinden werde.]
[Aus den 5 Reduktionslagen der Tafel
I (§ 64) wähle ich die Lage E,=
368 und aus den 4 Reduktionslagen der Tafel III (§ 65) die Lage E,=
60 mit dem Bemerken, daß die erstere die relativ schwächste,
die letztere die relativ stärkste Asymmetrie im Vergleiche mit den
übrigen Lagen aufweist. Für beide Tafeln werden nun sowohl mit
Bezug auf A die Werte t = D :h![]() und hiernach F [t] als auch mit Bezug
auf Dp die
Werte t' = ¶' : e¢
und hiernach F [t] als auch mit Bezug
auf Dp die
Werte t' = ¶' : e¢![]() und t,= ¶,:
e,
und t,= ¶,:
e,![]() und hiernach F[t¢]
und F [t,]
berechnet, wo die D , ¶'
,
¶, von
A oder Dp aus
bis zu den jeweiligen Intervallgrenzen a ± ½i
(nicht bis zu den a selbst) sich erstrecken. Es werden sodann die
Differenzen der aufeinanderfolgenden F -Werte,
die als j -Werte zu bezeichnen sind, gebildet
und die gefundenen j[t] mit ½m
, die j [t'] resp. j
[t,] mit m'
resp.
m,
multipliziert.
Auf diese Weise resultieren die nach dem einfachen und nach dem zweiseitigen
G. G. berechneten z-Werte im Vergleich mit den beobachteten Tafelwerten
in den beiden folgenden Tabellen. Hierbei sind die Zahlenwerte von h,
e¢
und e,ohne
Korrektion zu Grunde gelegt, da die Anbringung derselben bei der Größe
des m und dem angestrebten Genauigkeitsgrade belanglos ist:
und hiernach F[t¢]
und F [t,]
berechnet, wo die D , ¶'
,
¶, von
A oder Dp aus
bis zu den jeweiligen Intervallgrenzen a ± ½i
(nicht bis zu den a selbst) sich erstrecken. Es werden sodann die
Differenzen der aufeinanderfolgenden F -Werte,
die als j -Werte zu bezeichnen sind, gebildet
und die gefundenen j[t] mit ½m
, die j [t'] resp. j
[t,] mit m'
resp.
m,
multipliziert.
Auf diese Weise resultieren die nach dem einfachen und nach dem zweiseitigen
G. G. berechneten z-Werte im Vergleich mit den beobachteten Tafelwerten
in den beiden folgenden Tabellen. Hierbei sind die Zahlenwerte von h,
e¢
und e,ohne
Korrektion zu Grunde gelegt, da die Anbringung derselben bei der Größe
des m und dem angestrebten Genauigkeitsgrade belanglos ist:
Vergleich der empirischen z von Tafel I (Vertikalumfang des Schädels) mit den theoretischen nach einfachem und zweiseitigem G. G.
E = 1 mm ; i = 5 ; A = 408,2 ; Dp = 409,7 ; h = 11,1 ; e' = 10,4 ; e,= 11,9 ; m = 450 ; m' = 210 ; m,= 240 .
|
a
|
empirische z
|
|
|
||
|
|
|
|
|
||
| 363 | | 0,5 | 0,5 | + 0,5 | + 0,5 |
| 368 | l | 1 | 1 | 0 | 0 |
| 373 | 2 | 3 | 3 | + 1 | + 1 |
| 378 | 5 | 6 | 7 | + 1 | + 2 |
| 383 | 17 | 13 | 13 | - 4 | - 4 |
| 388 | 24 | 22,5 | 22,5 | - 1,5 | - 1,5 |
| 393 | 36 | 35,5 | 34,5 | - 0,5 | - 1,5 |
| 398 | 41 | 49 | 47 | + 8 | + 6 |
| 403 | 59 | 60 | 58 | + 1 | - 1 |
| 408 | 65 | 64 | 64 | - 1 | - 1 |
| 413 | 65 | 60 | 62 | - 5 | - 3 |
| 418 | 51 | 50 | 52 | - 1 | + 1 |
| 423 | 40 | 37 | 38 | - 3 | - 2 |
| 428 | 17 | 24 | 24 | + 7 | + 7 |
| 433 | 19 | 13 | 13 | - 6 | - 6 |
| 438 | 4 | 7 | 6 | + 3 | + 2 |
| 443 | 2 | 3 | 3 | + 1 | + 1 |
| 448 | 2 | 1 | 1 | - 1 | - 1 |
| 453 | | 0,5 | 0,5 | + 0,5 | + 0,5 |
| Summe | 450 | 450 | 450 | 46 | 42 |
Vergleich der empirischen z von Tafel III (Rekruten) mit den theoretischen nach einfachem und zweiseitigem G. G.
E = 1 Zoll ; i = 1 , A = 71,75 ; Dp = 71,99 ; h = 2,04 ; e¢ = 1,92 ; e,= 2,16 ; m = 2047 ; m' = 963,5 ; m,= 1083,5 .
|
|
|
|
|
||
|
|
|
|
|
||
| 60 | 1 | | | - l | - 1 |
| 61 | 0 | | | 0 | 0 |
| 62 | 0 | | 0,5 | 0 | + 0,5 |
| 63 | 0 | 1 | 1,5 | + 1 | + 1,5 |
| 64 | 2 | 3,5 | 4 | + 1,5 | + 2 |
| 65 | 15,5 | 10 | 12 | - 5,5 | - 3,5 |
| 66 | 26 | 26 | 28 | 0 | + 2 |
| 67 | 54 | 58 | 59 | + 4 | + 5 |
| 68 | 108 | 110 | 108 | + 2 | 0 |
| 69 | 172 | 179 | 174 | + 7 | + 2 |
| 70 | 253 | 252 | 243 | - 1 | - 10 |
| 71 | 290 | 304 | 298 | + 14 | + 8 |
| 72 | 330,5 | 315 | 318 | - 15,5 | - 12,5 |
| 73 | 296 | 282 | 291 | - 14 | - 5 |
| 74 | 223,5 | 217 | 226 | - 6,5 | + 2,5 |
| 75 | 142 | 143 | 145,5 | + 1 | + 3,5 |
| 76 | 75 | 81 | 80,5 | + 6 | + 5,5 |
| 77 | 38 | 40 | 37 | + 2 | - 1 |
| 78 | 13 | 17 | 15 | + 4 | + 2 |
| 79 | 3,5 | 6 | 5 | + 2,5 | + 1,5 |
| 80 | 2 | 2 | 1 | 0 | - 1 |
| 81 | 1 | 0,5 | | - 0,5 | - 1 |
| 82 | 0,5 | | | - 0,5 | - 0,5 |
| 83 | 0,5 | | | - 0,5 | - 0,5 |
| Summe | 2047 | 2047 | 2047 | 90 | 72 |
Wie man sieht, ist in beiden Tabellen die Gesamtsumme der Abweichungen zwischen beobachteten und berechneten Werten, dem absoluten Betrage nach genommen, für das zweiseitige Gesetz kleiner als für das einfache, wenn schon der Unterschied namentlich für die erste Vergleichstabelle unbedeutend ist. Was aber mehr ins Gewicht fällt, ist die größere Treue, die durch das zweiseitige Gesetz im Vergleiche zum einfachen in der Darstellung des Kernes beider Tafeln, den Endabteilungen gegenüber, erzielt wird.]
[Übrigens zeigt der Vergleich der z-Werte des zweiseitigen Gesetzes mit den entsprechenden z-Werten des einfachen Gesetzes in beiden Fällen übereinstimmend, daß von der Tafelmitte aus für wachsende a jene zuerst größer und dann kleiner, für abnehmende a jene zuerst kleiner und dann größer als diese sind. Der Grund hierfür liegt in der beiden Tafeln gemeinsamen Richtung der Asymmetrie, und es würden sich diese Verhältnisse gerade umkehren, wenn die Asymmetrie die entgegengesetzte Richtung erhielte.]