§ 112. Gehen wir jetzt an die Bestimmung der Wahrscheinlichkeitsverhältnisse des zufälligen Unterschiedes, welcher zwischen der Zahl der positiven und negativen Abweichungen von einem Mittelwerte aus einer endlichen Zahl von Werten zu erwarten ist, wenn die Wahrscheinlichkeit der Abweichungen vom wahren Mittel, wie es aus einer unendlichen Zahl von Werten folgen würde, nach beiden Seiten gleich groß ist. Indem der falsche, d. i. aus dem endlichen m gewonnene Mittelwert vom wahren um eine zufällige (bei verschiedenen Serien bald nach einer, bald nach der anderen Seite gehende) Größe abweicht, sind auch die Abweichungen D von beiden Mitteln in jeder Serie verschieden; und es bleibt zwar auch bei Rechnung vom falschen Mittel die gleiche W. der + D und - D bestehen, wenn sie für das wahre Mittel bestand, aber die Wahrscheinlichkeitsverhältnisse des Unterschiedes v zwischen der Zahl derselben ändern sich. Dies begreift sich leicht nach der in § 109 angestellten Betrachtung, da das falsche Mittel durch die Bedingung bestimmt wird, daß die Summe der Abweichungen davon nach beiden Seiten gleich gemacht wird, indes sie bei Rechnung von dem unbekannten wahren Mittel bei endlichem m im allgemeinen als ungleich vorauszusetzen ist. Durch diese künstliche Ausgleichung der Summen der + D und - D würden auch die Zahlen derselben ausgeglichen werden, wenn Zahl und Summe proportionale Änderungen erlitten, was nicht der Fall ist; jedenfalls aber wird der Unterschied v durch den Übergang vom wahren zum falschen Mittel gegen den Unterschied u verkleinert.
Um zu beurteilen, in welchem Verhältnisse diese Verkleinerung nach W. zu erwarten, muß ein bestimmtes Gesetz der Verteilung der wahren D nach Zahl und Größe zu Grunde gelegt werden, weil hiervon die Wahrscheinlichkeitsverhältnisse des Unterschiedes zwischen wahrem und falschem Mittel abhängen, hiervon aber wieder die Wahrscheinlichkeitsverhältnisse des Unterschiedes v . Nun ist bekannt, daß für die Abweichungen, welche die Einzel-exemplare von K.-G. bei nicht zu unregelmäßiger Verteilung bezüglich ihres Mittelwertes zeigen, das durch das Integral F (s. Kap. XVII) bestimmte Gesetz der Fehlerwahrscheinlichkeit zu Grunde gelegt werden kann, wenn man ein großes m und approximative Symmetrie hat, und somit wird dies Gesetz auch im Folgenden zu Grunde gelegt werden.
§ 113. Eine Untersuchung über
diese Verhältnisse liegt bisher überhaupt weder vor, noch reichen
die mir bisher bekannten Voruntersuchungen hin, die Aufgabe vollständig
danach zu behandeln. Inzwischen findet man im Zusatz (§ 116) eine
Untersuchung von mir geführt, wonach approximativ das mit Q2
zu bezeichnende mittlere Quadrat des Unterschiedes
v gleich m(1 - 2 : p ) sich ergibt, und
nachdem die weiterhin mitzuteilende Erfahrungsprobe gezeigt hat, daß
diese Bestimmung selbst bis zu einem m = 4 herab sehr approximativ
genügt, ließ sich fragen, ob aus dem Werte von Q
sich die übrigen Wahrscheinlichkeitsverhältnisse
von v entsprechend ableiten lassen, als bei der Rechnung vom wahren
Mittel die Wahrscheinlichkeitsverhältnisse von u aus dem Werte
Q = ![]() . Auch dies hat sich nach Erfahrung mit genügender Approximation
bestätigt. Und zwar ist für den wahrscheinlichen Wert von v
, welcher V heiße
[falls man die interpolationsmäßige Bestimmung zum Vergleiche
heranzieht], ebenso wenig eine Korrektion nach dieser Ableitung nötig
als für den Wert von V bei Ableitung von Q ; für
das einfach mittlere v aber, welches U
heiße, eine nur etwas größere Korrektion,
als für das einfach mittlere u , welches wir U nannten.
Endlich berechnet sich auch die Verteilungstafel der einzelnen v nach
Zahl und Größe approximativ genug nach dieser Voraussetzung.
. Auch dies hat sich nach Erfahrung mit genügender Approximation
bestätigt. Und zwar ist für den wahrscheinlichen Wert von v
, welcher V heiße
[falls man die interpolationsmäßige Bestimmung zum Vergleiche
heranzieht], ebenso wenig eine Korrektion nach dieser Ableitung nötig
als für den Wert von V bei Ableitung von Q ; für
das einfach mittlere v aber, welches U
heiße, eine nur etwas größere Korrektion,
als für das einfach mittlere u , welches wir U nannten.
Endlich berechnet sich auch die Verteilungstafel der einzelnen v nach
Zahl und Größe approximativ genug nach dieser Voraussetzung.
Die demgemäßen fundamentalen Bestimmungen sind folgende:
Q² =![]() m = 0,36338 m ; log 0,36338
= 0,56036 1 ; (1)
m = 0,36338 m ; log 0,36338
= 0,56036 1 ; (1)
Q=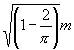 = 0,60281
= 0,60281![]() ; log
0,60281 = 0,78018 1 ; (2)
; log
0,60281 = 0,78018 1 ; (2)
U = 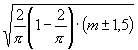 = 0,48097
= 0,48097![]() ;
log = 0,68212 1 ; (3)
;
log = 0,68212 1 ; (3)
V = 0,40659 ![]() ; log 0,40659 = 0,60916 1 . (4)
; log 0,40659 = 0,60916 1 . (4)
Zur Bestimmung von W[±v] hat man die Differenz der F Werte zu nehmen, welche in der Tabelle der t zu
![]() und
und ![]()
gehören, wo für Q
der obige Wert zu substituieren ist; für W[v
= 0] inbesondere aber den zu t = 1: Q![]() gehörigen F -Wert. Ww
[v] , d. i. die W.,
daß der gegebene Wert von v nicht erreicht wird, findet man
als den F -Wert, welcher zu t = (v
- 1) : Q
gehörigen F -Wert. Ww
[v] , d. i. die W.,
daß der gegebene Wert von v nicht erreicht wird, findet man
als den F -Wert, welcher zu t = (v
- 1) : Q![]() und Wa [v] , d. i.
die für v selbst und die unterhalb v gelegenen Werte
bestehende W., als den, welcher zu (v + 1) : Q
und Wa [v] , d. i.
die für v selbst und die unterhalb v gelegenen Werte
bestehende W., als den, welcher zu (v + 1) : Q![]() gehört.
gehört.
In der Formel für U gilt das obere Vorzeichen der Korrektion ± 1,5 für ungerades, das untere für gerades m , und eine Folgerung dieser Korrektion, sowie der Grund derselben ist das erfahrungsmäßige Datum, wofür jedoch die Theorie noch zu suchen, daß jeder Wert von U für ein gerades m merklich übereinstimmt mit dem um drei Einheiten kleineren Werte von U für ein ungerades m , wozu die Belege unten folgen.
Leider stehen bis jetzt zur Kontrolle für diese Approximationsformeln bezüglich v nicht ebenso, wie bezüglich deren für u im vorhergehenden Kapitel genaue Formeln für kleines m zu Gebote; ein um so fühlbarerer Mangel, als die theoretische Begründung und Ableitung obiger Formeln im Zusatz lückenhaft ist, und die Korrektion für U sogar sonderbar erscheinen kann. Ich würde daher dieselben mit wenig Zutrauen darbieten, wenn ich nicht durch eine sehr ausgedehnte empirische Bewährung diesen Mangel insoweit zu ersetzen vermocht hätte, daß man sicher sein kann, bei Benutzung derselben keinen in Betracht kommenden Irrtum zu begehen, wennschon eine genauere Begründung und Revision der Theorie durch einen Mathematiker von Fach sehr erwünscht wäre.
Die empirische Bewährung beruht wie die der früheren Funktionswerte von u auf einer Benutzung von Lotterielisten, welche aber ohne Vergleich umständlicher war als für die Werte des vorigen Kapitels. Denn es galt dazu, zuvörderst die Nummern jeder Liste in Werte von + D und - D in der Art zu übersetzen, daß für die ganze Liste die dem Integral F entsprechende Verteilung nach Zahl und Größe bei Rechnung vom wahren Mittel herauskam, welche durch die t- Tabelle im Anhang §183 repräsentiert ist; dann für jede zufällige Serie solcher Abweichungen von gegebenem m das falsche Mittel zu bestimmen, die positiven und negativen Abweichungen von diesem falschen Mittel zu rechnen und den Unterschied zwischen der Zahl beider als v zu nehmen. Etwas ausführlicher ist hiervon im Zusatz (§ 117) gehandelt und das Beispiel einer Bestimmung von v für eine zufällig genommene Serie mit m = 6 daselbst gegeben.
§ 114. Hiernach lasse ich zuvörderst
in einigen Tabellen die Gesamtheit der empirischen Data folgen, welche
ich bezüglich unserer Aufgabe direkt erhielt, um nachher die daraus
abgeleiteten Hauptwerte zusammengestellt mit den nach obigen Formeln berechneten
Werten anzuschließen. Wenn vielfach Zahlenangaben mit einem Bruchwerte
0,5 vorkommen, so rührt dies daher, daß, wenn zufällig,
wie dies mitunter vorkam, das falsche Mittel mit einem wahren Abweichungswerte
genau zusammentraf, die Abweichung vom falschen Mittel mit + 0,5 und -
0,5 nach beiden Seiten gezählt werden mußte, wodurch ein v
entstand, was in die Mitte zwischen die um je 2 distanten Werte der
v-Skala fiel, dann aber mit je 0,5 auf die beiden Nachbarwerte verteilt
wurde.
I. Zahl z , wie oft ein Unterschied v zwischen der Zahl der positiven und negativen Abweichungen vom falschen Mittel aus m Werten bei n-maliger Wiederholung der Bestimmung vorkam.
a) bei ungeradem m
| v | m = 5
n =2400 |
m = 7
n = 1700 |
m = 9
n = 1320 |
m = 11
n = 820 |
m = 13
n = 840 |
n =15 1)
n = 800 |
m = 17
n = 600 |
m = 19
n = 600 |
| 1 | 2155,5 | 1388,5 | 966,5 | 552 | 562,5 | ? | 351 | 327,5 |
| 3 | 244,5 | 300,5 | 324,5 | 235,5 | 231,5 | ? | 187 | 197,5 |
| 5 | | 11 | 29 | 32,5 | 41,5 | ? | 57 | 63 |
| 7 | | | | | 4,5 | ? | 5 | 10 |
| 9 | | | | | | | | 2 |
b) bei geradem m
| v | m = 4
n = 3000 |
m =
6
n =2000 |
m = 8
n =1500 |
m = 10
n = 1200 |
m =12
n =1000 |
m = 14
n = 850 |
m = 16
n =750 |
m = 18
n = 660 |
m = 20
n = 600 |
| 0 | 1950 | 1040 | 648 | 494 | 379 | 314 | 247 | 179,5 | 176 |
| 2 | 1050 | 905 | 753,5 | 588 | 489 | 382,5 | 333 | 325,5 | 256,5 |
| 4 | | 55 | 96,5 | 112 | 126 | 127,5 | 148 | 120 | 130,5 |
| 6 | | | 2 | 6 | 6 | 25 | 20 | 28 | 33 |
| 8 | | | | | | 1 | 2 | 7 | 3 |
| 10 | | | | | | | | | 1 |
1) [Die Werte dieser Kolumne waren durch unaufhebbare Widersprüche
entstellt]
II. Dieselben Angaben für einige größere Werte von m .
| v | m = 30
n = 400 |
m = 50
n = 240 |
m = 100
n = 120 |
m = 500
n = 24 |
| 0 | 94 | 49 | 19 | 2 |
| 2 | 169 | 84 | 31 | 2 |
| 4 | 90 | 51 | 13 | 3 |
| 6 | 36 | 32 | 22 | 3 |
| 8 | 8 | 14 | 18 | 2 |
| 10 | 3 | 8 | 9 | 2 |
| 12 | | 3 | 5 | 2 |
| 14 | | | 2 | 5 |
| 16 | | | 1 | 0 |
| 24 | | | | 1 |
| 28 | | | | 1 |
| 34 | | | | 1 |
Dieselben Serien mit m = 10
, 50 , 100 hatten bei Rechnung der Abweichungen vom wahren Mittel
folgende Resultate gegeben, welche also ganz direkt mit den vorigen, vom
falschen Mittel gerechneten vergleichbar sind, indes die in § 107
angeführten Resultate unter Zuziehung noch anderer Serien, daher mit
größerem n , gefunden sind.
III. Mit den vorigen Tabellen vergleichbare Tabelle für den Unterschied u bei Rechnung vom wahren Mittel.
| u | m = 10
n = 1200 |
m = 50
n = 240 |
m = 100
n = 120 |
| 0 | 301 | 23 | 10 |
| 2 | 467 | 52 | 17 |
| 4 | 299 | 44 | 14 |
| 6 | 102 | 42 | 13 |
| 8 | 29 | 28 | 22 |
| 10 | 2 | 16 | 16 |
| 12 | | 17 | 10 |
| 14 | | 7 | 2 |
| 16 | | 10 | 5 |
| 18 | | 0 | 4 |
| 20 | | 1 | 2 |
| 22 | | | 4 |
| 28 | | | 1 |
In den beiden Tabellen für Rechnung
vom falschen Mittel ist die Zahl z¢,
wie oft ein v das gleiche Vorzeichen mit der Abweichung des falschen
vom wahren Mittel hatte, und die Zahl z,,
wie oft es das entgegengesetzte Vorzeichen hatte, kurz, wie oft ein v
mit dem falschen A gleichseitig oder ungleichseitig war, zur
Zahl z = z' + z,zusammengezogen.
Geben wir jetzt die Werte z =
z' - z,für die Werte von m
= 6 bis m = 30, da für die anderen die Sonderung von z'
und z, nicht geschehen ist. Unter å
(± z) ist eine Summe
der z nach absolutem Werte,
unter åz
mit Rücksicht auf das Vorzeichen verstanden.
IV. Unterschied z = z¢ - z, zwischen der Zahl z' der mit dem falschen Mittel gleichseitigen und der Zahl z, der damit ungleichseitigen Werte von v gleicher Größe, welche sich zum z in vorigen Tabellen vereinigen, von m = 6 bis m = 30.
a) bei ungeradem m
|
|
|
|
|
|
|
|
|
|
|
n = 1700 | n = 1320 | n= 820 | n = 840 | n = 800 | n = 600 | n = 600 |
| 1 | + 33,5 | + 0,5 | - 33 | - 25,5 | + 29 | + 1 | - 20,5 |
| 3 | + 46,5 | - 4,5 | + 9,5 | + 21,5 | - 7 | - 10 | + 11,5 |
| 5 | 0 | + 1 | - 0,5 | - 8,5 | + 7,5 | - 5 | - 15 |
| 7 | | | | + 0,5 | + 1,5 | + 3 | - 4 |
| 9 | | | | | | | - 2 |
| å(±z) | 80 | 6 | 43 | 56 | 45 | 19 | 53 |
| å (z) | + 80 | - 3 | - 24 | - 12 | + 31 | - 11 | - 30 |
|
|
|
|
|
|
|
|
|
|
m =30 |
|
|
n = 2000 | n = 1500 | n = 1200 | n = 1000 | n = 830 | n = 750 | n = 660 | n = 600 | n= 400 |
| 2 | - 24 | +42,5 | + 20 | + 8 | +1,5 | - 29 | - 35,5 | - 16,5 | +5 |
| 4 | +13 | +11,5 | + 16 | + 8 | +0,5 | - 14 | - 8 | + 1,5 | 0 |
| 6 | | 0 | - 4 | 0 | +3 | + 2 | + 2 | - 1 | + 4 |
| 8 | | | | | +1 | + 2 | + 1 | - 3 | - 2 |
| 10 | | | | | | | | - 1 | - 1 |
| å(±z) | 37 | 54 | 40 | 16 | 6 | 47 | 46,5 | 23 | 12 |
| å (z) | - 11 | +54 | +32 | +16 | + 6 | - 39 | - 40,5 | - 20 | + 6 |
Es kann etwas auffällig erscheinen, daß die Werte von z und mithin auch åz bei den kleineren, namentlich geradzahligen Werten m fast alle positiv sind. Wahrscheinlich aber hat dies denselben Grund, der für eine analoge Erscheinung (§ 107) geltend gemacht wurde, daß nämlich die Serien mit kleinerem m in die Serien mit größerem m mit eingehen, so daß die Serien mit verschiedenem m nicht ganz unabhängig von einander sind, indes aber nicht nur jede Serie für sich, die ein v gab, sondern alle n-Serien für ein gegebenes m zusammen rein nach Zufall geordnet sind.
§ 115. Aus den ersten beiden Tabellen
leiten sich folgende Hauptwerte ab, deren Zusammenstellung mit den beistehenden
theoretischen Werten, nach obigen Formeln, zur Prüfung dieser Formeln
dienen kann.
|
|
|
|
|
|||
| beobachtet | 0,36338 m | Beobachtet | 0,48097 |
beob.2) | 0,40659 |
|
| 4 | 1,40 | 1,45 | 0,70 | 0,76 | 0,72 | 0,81 |
| 5 | 1,82 | 1,82 | 1,20 | 1,23 | 0,89 | 0,91 |
| 6 | 2,25 | 2,18 | 1,02 | 1,02 | 0,96 | 1,00 |
| 7 | 2,57 | 2,54 | 1,38 | 1,40 | 1,03 | 1,08 |
| 8 | 3,09 | 2,91 | 1,27 | 1,23 | 1,19 | 1,15 |
| 9 | 3,49 | 3,27 | 1,58 | 1,56 | 1,21 | 1,22 |
| 10 | 3,63 | 3,63 | 1,38 | 1,40 | 1,27 | 1,29 |
| 11 | 4,25 | 4,00 | 1,73 | 1,70 | 1,36 | 1,35 |
| 12 | 4,19 | 4,36 | 1,52 | 1,56 | 1,38 | 1,41 |
| 13 | 4,65 | 4,72 | 1,78 | 1,83 | 1,37 | 1,47 |
| 14 | 5,33 | 5,09 | 1,69 | 1,70 | 1,46 | 1,52 |
| 15 | ? 3) | 5,45 | ? | 1,95 | ? | 1,57 |
| 16 | 6,06 | 5,81 | 1,86 | 1,83 | 1,65 | 1,63 |
| 17 | 6,17 | 6,18 | 2,05 | 2,07 | 1,64 | 1,68 |
| 18 | 7,09 | 6,54 | 2,05 | 1,95 | 1,78 | 1,73 |
| 19 | 7,22 | 6,90 | 2,21 | 2,18 | 1,80 | 1,77 |
| 20 | 7,66 | 7,27 | 2,11 | 2,07 | 1,85 | 1,82 |
| 30 | 10,06 | 10,90 | 2,27 | 2,57 | 2,14 | 2,23 |
| 50 | 17,87 | 18,17 | 3,25 | 3,35 | 2,63 | 2,88 |
| 100 | 37,87 | 36,34 | 4,87 | 4,77 | 4,64 | 4,07 |
| 500 | 178,17 | 181,69 | 10,42 | 10,74 | 9,00 | 9,09 |
3) [Vergl. die Bemerkung zu Tab. I a.]
[Berücksichtigt man neben den
Tabellen I und II die Vergleichstabelle III, so findet man folgende, mit
einander vergleichbare Hauptwerte für den Ausgang vom wahren und vom
falschen Mittel:
| m | Q² | Q² | U | U | V | V |
| 10 | 10,32 | 3,63 | 2,495 | 1,38 | 2,19 | 1,27 |
| 50 | 52,48 | 17,87 | 5,825 | 3,25 | 5,04 | 2,63 |
| 100 | 97,47 | 37,87 | 8,00 | 4,87 | 7,49 | 4,64 |
Dieselben zeigen, daß der Übergang vom wahren
zum falschen Mittel in der Tat eine Verringerung der mittleren und wahrscheinlichen
Unterschiede mit sich führt, die in genügender Übereinstimmung
mit der theoretisch geforderten Verringerung steht. Es ist nämlich:
| m | Q² : Q² | U : V | V : V |
| 10 | 0,352 | 0,554 | 0,577 |
| 50 | 0,341 | 0,558 | 0,522 |
| 100 | 0,389 | 0,608 | 0,619 |
Die theoretischen Verhältnisse dagegen sind ohne Berücksichtigung der Korrektionen für U und U , Q2: Q² = 0,363; U : U = V : V = 0,603.]
Man kann es als eine Merkwürdigkeit anführen, daß der Wert U , welcher für Rechnung vom falschen Mittel gilt, nahe übereinkommt mit der einfach mittleren Abweichung von dem für Rechnung vom wahren Mittel geltenden U , oder daß U nahe gleich e [U] , doch nur bei so großem m , daß die Korrektion ± 1,5 nicht mehr erheblich in Betracht kommt. Dies ergibt sich sowohl aus dem Vergleiche der Formeln für beide Werte:
[Auf Grund der obigen Zusammenstellung der Werte von U und U insbesondere ergibt sich e[U] für m = 10; 50; 100 resp. gleich: 1,64; 3,44; 4,40. Es ist somit in der nämlichen Reihenfolge e [U] - U resp. gleich: 0,26; 0,19; - 0,47.]
Auch kann man nicht versichern, ob
der Zahlenkoeffizient für beide Werte nicht wirklich mit Vorteil als
gleich anzunehmen ist, da beide auf verschiedenen Wegen abgeleitete und
hiernach etwas verschieden sich ergebende Koeffizienten beiderseits überhaupt
nur Approximativbestimmungen liefern, mithin keine absolute Gültigkeit
haben.
4) [Vergl. § 120 im folg. Kap. Da nach der dortselbst gegebenen Bestimmung e [U] = 0,60488 U und da andererseits mit Vernachlässigung der Korrektion:
0,60488 gleich ![]()
gesetzt werden kann.]
Wahrscheinlich erstrecken sich dergleichen Beziehungen auch auf die anderen Hauptwerte, und die mitgeteilten Beobachtungsdata geben die Gelegenheit, es zu prüfen; doch habe ich unterlassen, darauf einzugehen, teils in Erwartung, daß sich die Theorie erst dieses Verfahrens mehr bemächtige, teils um nicht die schon so weitläufige Untersuchung noch weiter auszudehnen.
Endlich folgt hier noch der Vergleich
einiger Verteilungstafeln nach Rechnung und Erfahrung.
Vergleich der beobachtetenZahlen von v in obigen Tabellen mit den nach § 113 berechneten für einige Werte von m .
|
|
|
|
|
|
|
|||||
|
|
beob. | ber. | beob. | ber. | Beob. | ber. | beob. | ber. | beob. | ber. |
| 0 | 1950 | 1779 | 494 | 480 | 176 | 174 | 94 | 95 | 49 | 44,5 |
| 2 | 1050 | 1182 | 588 | 581 | 256,5 | 267 | 169 | 159,5 | 84 | 80 |
| 4 | | 38 | 112 | 128 | 130,5 | 121 | 90 | 93,5 | 51 | 57,5 |
| 6 | | | 6 | 10 | 33 | 32 | 36 | 38,5 | 32 | 33,5 |
| 8 | | | | | 3 | 6 | 8 | 13 | 14 | 16 |
| 10 | | | | | 1 | | 3 | 0,5 | 8 | 6 |
| 12 | | | | | | | | | 2 | 2 |
| 14 | | | | | | | | | | 0,5 |
§116. [Erster Zusatz. Die theoretische Bestimmung des mittleren und wahrscheinlichen Wertes von v .]
[Jedem Systeme von m positiven oder negativen Größen D1, D2 ... Dm gehört ein Mittelwert D0 und ein Differenzwert v zu, welch letzterer angibt, um wie viel die Anzahl v 5) der oberhalb D0 liegenden Werte die Anzahl µ der unterhalb D0 liegenden Werte übersteigt. Die Werte von v = v - µ können daher jeden Wert der Reihe: m 2 , m 4 .... 4 m , 2 - m darstellen, so daß es im ganzen m 1 positive oder negative v-Werte gibt, während die entsprechende Anzahl der u-Werte m + 1 beträgt. Hierbei bedarf der Fall, wo ein Di (i = 1, 2 ... m) mit D0 zusammenfällt, keiner besonderen Rücksichtnahme, da er bei der vorauszusetzenden stetigen Veränderlichkeit dieser Größen als ein Grenzfall anzusehen ist, der entweder dem Falle, daß Di oberhalb D0 oder dem Falle, daß Di unterhalb D0 liegt, beizuzählen ist. So ist beispielsweise für m = 2 der Wert von v stets gleich Null; für m = 3 dagegen ist v entweder gleich + 1 oder gleich - 1.]
[Bezeichnet D0 den zwischen - ¥ und + ¥ variierenden Mittelwert, stellt ferner deine positive Größe dar, die alle Werte von 0 bis ¥ annehmen kann, und repräsentieren schließlich a1 , a2 ... aµ-1 ; b1 , b2 ... bv-1 unabhängig von einander die positiven Werte von 0 bis 1, so setze man:
D1 = D0 - (1 - a1) d
D2 = D0 - (1 - a2) a1d
. . . . . . . . . . . . . . .
Dµ-1 = D0 - (1 - aµ-1) aµ-2 . . a1 d
Dµ = D0 - aµ-1 aµ-2 . . a1 d(5)
Dµ+1 = D0 + (1 - b1) d
Dµ+2 = D0 + (1 - b2)b1 d
. . . . . . . . . . . . . . .
Dm-1 = D0 - (1 - bv-1) bv-2 . . b1 d
Dm = D0 - bv-1 bv-2 . . b1 d.
Man erhält so zunächst alle Wertensysteme D1 ... Dm , deren µ ersten Werte unterhalb des jeweiligen Mittelwertes liegen, während die v letzten Werte denselben übersteigen. In der Tat ist auf Grund der festgesetzten Variabilitätsbereiche D1, D2 . . Dµ kleiner als D0 ; Dµ+1 , Dµ+2 . . . Dm größer als D0 ; so ist ferner die Summe der µ ersten D gleich µD0 - d und die Summe der v letzten D gleich vD0 + d , somit die Summe aller D gleich m D0 .]
[Um sodann alle Wertensysteme D1, D2 . . Dm zu erhalten, für welche irgend welche Werte in der Anzahl µ unterhalb und die übrigen v oberhalb des jeweiligen Mittelwertes liegen, ist nur nötig, an dem Systeme (5) alle möglichen Vertauschungen zwischen den µ ersten und den v letzten D vorzunehmen, was zu m! : (µ! v!) Gleichungensystemen von der Form (5) führt, deren jedes die nämliche Mannigfaltigkeit von Wertensystemen D1, . . Dm nur mit jedesmal veränderter Reihenfolge der D darstellt, und deren Verein die Gesamtmannigfaltigkeit der zu v = v - µ gehörenden Wertensysteme bestimmt.]
[Es sollen nun die Di
(i = 1 . . . m) als Abweichungen
vom wahren Mittel aufgefaßt werden, für welche das G. G. gilt.
Dann ist die W. für das Vorkommen eines einzelnen Wertes D
gleich: ![]() .
.
Es ist ferner die W. für das Vorkommen des Systems der m Werte D1 . . . Dm gleich:
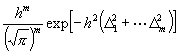 ;
;
da nach bekanntem Satze der Wahrscheinlichkeitsrechnung die W. für das Zusammentreffen mehrerer, von einander unabhängiger Ereignisse gleich dem Produkte der W. für das Eintreffen jedes einzelnen Ereignisses ist. Es ist schließlich die W. für das Vorkommen irgend eines Systemes D1 . . . Dm , das einer wohl definierten, stetigen Mannigfaltigkeit solcher Systeme angehört, gleich:
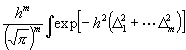 dD1
. . . dDm
(6)
dD1
. . . dDm
(6)
wo das Integral über das Kontinuum der Wertensysteme zu erstrecken ist, in dessen Bereich das vorkommende Wertensystem fallen soll. Denn die W. dafür, daß irgend eines aus einer Reihe einander ausschließender Ereignisse eintritt, ist wie die Wahrscheinlichkeitsrechnung lehrt gleich der Summe der W. der einzelnen Ereignisse.]
![]() ,
,
Man erhält somit als Ausdruck für die W., daß von m Abweichungen D1 . . . Dm die µ ersten unterhalb, die v letzten oberhalb des Mittelwertes D0 liegen, das Integral:
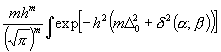 .
(8)
.
(8)
 ×
×
![]() ,
(9)
,
(9)
wo das Integral zwischen eben denselben Grenzen zu nehmen ist.]
[Da sich die Integration über D0 und über dsofort ausführen läßt, indem:
![]() ;
;
und für gerades m :
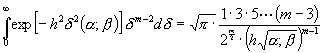 ;
;
für ungerades m :
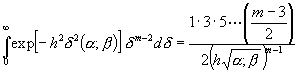 ;
;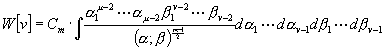 (10)
(10)für gerades m :
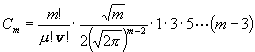 ;
;
für ungerades m :
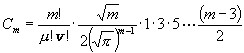 ;
;
und wo die Integration für jedes aund bvon der unteren Grenze 0 bis zur oberen Grenze 1 zu erstrecken ist.]
[Die Formel (10) erprobt sich zunächst in den einfachsten Fällen für m = 2 und 3, deren W[0] resp. W[1] von vornherein bekannt ist. Es ist nämlich, da für m = 2 stets v = 0 ist, W[0] = 1 und, da v für m = 3 entweder gleich + 1 oder gleich - 1, und beide Werte gleich wahrscheinlich sind, W[+1] = W[-1] = ½. Und in der Tat erhält man aus (10) für m = 2 :
![]() ;
;
ferner für m = 3 :
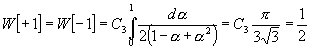 .]
.][Hiernach findet man für m = 4 :
![]() ;
; ![]() ;
;
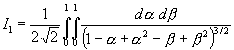
![]() ;
;
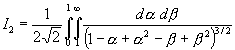
![]() .
.
Q²
= 1,40368 ; U = 0,70184 .
Q² = 1,7828 ; U = 1,1957 .
[Um aber auf diesem Wege in gleicher Weise, wie es im vorigen Kapitel für die Abweichungen vom wahren Mittel geschah, Formeln für W [v] und hiernach solche für Q2 , U und V zu gewinnen, welche die Abhängigkeit dieser Werte von m explicite darstellen, müßte das (m - 2)-fache Integral von (10) in allgemein gültiger Ausführung vorliegen. Nun läßt sich allerdings eine solche Ausführung, am bequemsten aus (9), durch Entwicklung in Reihen gewinnen. Da dieselbe jedoch zu Weitläufigkeiten führt, so ist es angezeigt, den Wert von Q2 direkt zu bestimmen, um sodann mit dem Zugeständnis, daß so eine für die hier verfolgten Ziele unbedenkliche Lücke bleibt U und V daraus unter der Voraussetzung abzuleiten, daß für große m die Wahrscheinlichkeitsverhältnisse der v durch das G. G. geregelt werden. Diese Voraussetzung ist zulässig, da nach (11) das Wahrscheinlichkeitsgesetz für v symmetrisch ist bezüglich des Maximalwertes v = 0 , und da ferner die aus dem G. G. folgenden Beziehungen zwischen Q2 , U und V , die den Formeln (1) bis (4) zu Grunde liegen, eine hinreichende empirische Bewährung gefunden haben. Es wird dann allerdings auch auf eine theoretische Begründung der für U gegebenen Korrektionen verzichtet.]
[Die direkte Bestimmung von Q2 läßt sich wie folgt erreichen. Man beachte, daß für ein beliebiges System von Abweichungen D1, D2 ... Dm , deren arithmetischer Mittelwert D0 sei, die Differenz v = v - µ zwischen den Anzahlen der oberhalb und unterhalb D0 liegenden Di (i = 1, 2.. m) darstellbar ist durch:
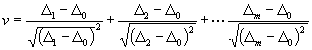 ;
(12)
;
(12)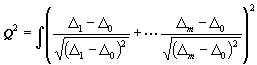
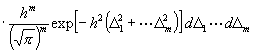 , (13)
, (13)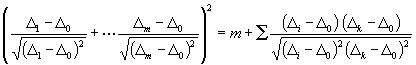
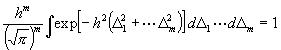 ,
,
und alle m (m - 1) Integrale:
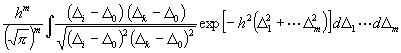
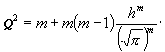
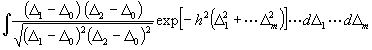 ,
(14)
,
(14)
wo die Grenzen der Integration, wie oben angegeben, zu nehmen sind.]
[Um nunmehr das m-fache Integral
auszuwerten, setze man:
D1 = D0 + d1
D 2 = D0 + d2
![]()
![]()
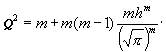
![]() ,
,
wo: ![]()
![]() (16)
(16)
Hieraus gewinnt man durch Ausführung der Integration bez. D0 , d3 ,d4 . . dm :
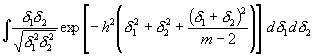 (17)
(17)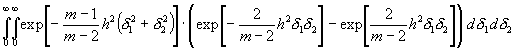 (18)
(18)
oder, wenn ![]() ;
; ![]() :
:
![]()
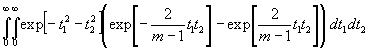 (19)
(19)
Nun ist:
![]()
![]()
Folglich resultiert schließlich, wenn t12 = t1 und t22 = t2 gesetzt wird:
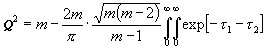
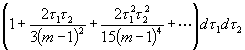 (20)
(20)
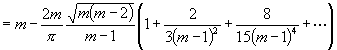
![]() ;
(21)
;
(21)
somit in erster Annäherung:
Hieraus folgen dann unmittelbar die Formeln (3) und (4) für U und V jedoch ohne die für U empirisch gefundene Korrektion wenn das G. G. für die Wahrscheinlichkeitsverhältnisse der v bei großem m in Anspruch genommen wird.]
§117. [Zweiter Zusatz. Erläuterungen zur empirischen Bewährung der Wahrscheinlichkeitsbestimmungen für Q , U und V mittelst der Lotterielisten.]
Zunächst könnte es überhaupt unmöglich scheinen, ein Prinzip empirischer Bewährung dafür zu finden, da ja die Formeln wesentliche Symmetrie und Gültigkeit des G. G. zufälliger Abweichungen voraussetzen; aber an welchem Gegenstande man auch die Bewährung versuchen will, man kann für die Abweichungen vom Mittel A weder die eine, noch die andere Bedingung von vornherein als erfüllt voraussetzen. Aber man kann sich künstlich einen Gegenstand herstellen, der diese Bedingungen erfüllt, nach folgendem Prinzip.
Denke man sich, um das Prinzip zuerst in möglichst faßlicher Form zu erläutern, in eine Urne eine sehr große Anzahl, ich will sagen 15 000 weiße und ebenso viele schwarze Kugeln getan, wovon die ersten als positive, die letzten als negative Abweichungen zählen mögen; es sollen diese Kugeln aber mit positiven und negativen Größenwerten beschrieben sein, jede Größe in solcher Wiederholung, wie es der W. der entsprechenden Fehlergrößen nach dem G. G. entspricht. Als richtiger Mittelwert, von dem die Fehler ihren Ausgang nehmen, gilt hierbei der Nullwert. Man ziehe nun m Kugeln und nenne positive Summe åD' die Summe, die man erhält, wenn man jede positive Fehlergröße mit der Zahl, wie oft sie gezogen ist, multipliziert; entsprechend mit der negativen Summe åD,. Sofern nun åD ' und åD,nach Zufall nicht gleich gefunden sind, erscheint der Mittelwert um (åD' - åD,) : m , welcher Wert c heiße, vermehrt oder vermindert, je nachdem åD' > åD, oder umgekehrt. Der falsche Mittelwert ist also statt 0 gleich ± c . Hat man also solchergestalt c bestimmt, so kann man jetzt zählen, wie viel Fehler größer und wie viel kleiner als c sind und hiernach ein ± (µ' - µ,) oder v für diesen Fall finden und, nachdem man n Züge getan hat, hieraus sowohl ein mittleres v als wahrscheinliches v finden, welches letztere nur eine Interpolation fordert.
Nun würde ein solches Verfahren mit der Urne und so vielen weißen und schwarzen, mit Größenwerten beschriebenen Kugeln praktisch undurchführbar sein; aber man kann die Urne durch das Lotterierad, die weißen und schwarzen Kugeln durch geradzahlige und ungeradzahlige Nummern ersetzt halten. Man kann ferner, um unter den 30 000 Nummern Verhältnisse herzustellen, welche den Wahrscheinlichkeitsverhältnissen der Fehler entsprechen, allen Nummern von 1 bis incl. 338 die Größe 0,25 beilegen, allen von da bis incl. 1015 die Größe 1, allen von da bis 1691 die Größe 2, allen von da bis 2366 die Größe 3 u. s. w. und diese Übersetzung in eine Tabelle bringen, welche bei jeder Lotterienummer, auf die man im Durchgehen der Liste trifft, sofort Auskunft gibt, welche Größe sie repräsentiert.
[Die Herstellung dieser Tabelle erfolgt
mittelst der t-Tabelle (§ 183), wie folgt. Zunächst ist
eine Entscheidung zu treffen, nach welchem Intervalle die zu Grunde zu
legenden t-Werte fortschreiten sollen. Im Interesse der Bequemlichkeit
werde das Intervall 0,02 , mit dem Anfangs-t = 0,01 , gewählt.
Da nun die vorausgesetzte Anzahl der Lotterienummern, die als ebensoviele
Exemplare eines K.-G. zu interpretieren sind, 30 000 ist, so sind die den
Intervallgrenzen entsprechenden F -Werte mit
30 000 zu multiplizieren, um in ihren sukzessiven Differenzen die Anzahlen
der Abweichungen zu erhalten, die in die aufeinander folgenden Intervalle
fallen. Die Abweichungen selbst aber sind, wie das für unsere K.-G.
durchweg geschieht, in der Mitte des Intervalles, in das sie gehören,
vereinigt zu denken. Es wäre somit, da t = D
: e![]() ,
das erste D gleich e
,
das erste D gleich e![]()
0,005 ; das zweite gleich e
0,005 ; das zweite gleich e![]()
0,02 ; das dritte gleich e
0,02 ; das dritte gleich e![]()
0,04 u.s.w. zu setzen; da jedoch die Größe der mittleren Abweichung
ebeliebig festgesetzt werden darf, so kann e
= 1 : 0,02
0,04 u.s.w. zu setzen; da jedoch die Größe der mittleren Abweichung
ebeliebig festgesetzt werden darf, so kann e
= 1 : 0,02![]() =
28,2095 angenommen werden, wonach das erste D
gleich 0,25 , das zweite D gleich
1 , das dritte gleich 2 u.s.w. gefunden wird. Um endlich diesen D
die Häufigkeit des Vorkommens, wie sie das G. G. gemäß
der t-Tabelle verlangt, zu sichern, sind jedem einzelnen so viele
Lotterienummern zuzuweisen, als die Anzahl der zugehörigen Abweichungen
beträgt. Diese Zuordnung könnte an sich ganz willkürlich
vorgenommen werden, da jede der 30 000 Nummern des Glücksrades die
nämliche W. besitzt, gezogen zu werden. Selbstverständlich
wird jedoch dabei die natürliche Reihenfolge der Nummern beobachtet;
es werden mithin dem ersten D die ersten 338
Nummern, dem zweiten D die 677 folgenden Nummern
u.s.w., wie oben angegeben, beigesellt, so daß eine Tabelle entsteht,
die auszugsweise folgendermaßen lautet:]
=
28,2095 angenommen werden, wonach das erste D
gleich 0,25 , das zweite D gleich
1 , das dritte gleich 2 u.s.w. gefunden wird. Um endlich diesen D
die Häufigkeit des Vorkommens, wie sie das G. G. gemäß
der t-Tabelle verlangt, zu sichern, sind jedem einzelnen so viele
Lotterienummern zuzuweisen, als die Anzahl der zugehörigen Abweichungen
beträgt. Diese Zuordnung könnte an sich ganz willkürlich
vorgenommen werden, da jede der 30 000 Nummern des Glücksrades die
nämliche W. besitzt, gezogen zu werden. Selbstverständlich
wird jedoch dabei die natürliche Reihenfolge der Nummern beobachtet;
es werden mithin dem ersten D die ersten 338
Nummern, dem zweiten D die 677 folgenden Nummern
u.s.w., wie oben angegeben, beigesellt, so daß eine Tabelle entsteht,
die auszugsweise folgendermaßen lautet:]
| Größe | Zahl | Größe | Zahl | Größe | Zahl |
| 0,25 | 1 338 | 14 | 8923 9548 | 47 | 24347 24626 |
| 1 | 339 1015 | 15 | 9549 10167 | ||
| 2 | 1016 1691 | 74 | 28872 28946 | ||
| 3 | 1692 2365 | 75 | 28947 29018 | ||
| 4 | 2366 3038 | 25 | 15351 15877 | ||
| 26 | 15878 16393 | ||||
| 5 | 3039 3708 | 27 | 16394 16899 | 100 | 29854 29865 |
| 28 | 16900 17394 | ||||
| 10 | 6356 7005 | ||||
| 11 | 7006 7650 | 143 | 29998 | ||
| 12 | 7651 8289 | 45 | 23756 24056 | 150 | 29999 |
| 13 | 8290 8922 | 46 | 24057 24346 | 160 | 30000 |
Eigentlich freilich ändern sich
die Abweichungen kontinuierlich, während hier jede Abweichungsgröße
um 1 von der folgenden abweicht; dieses Abweichungsintervall ist aber im
Verhältnisse zur einfachen mittleren Abweichung, also nach dem getroffenen
Verhältnisse 1 : 0,02 ![]() =
28,2095 klein genug, um ein merklich übereinstimmendes Resultat mit
kontinuierlicher Größenänderung zu geben.
=
28,2095 klein genug, um ein merklich übereinstimmendes Resultat mit
kontinuierlicher Größenänderung zu geben.
Es haben mir nun sächsische Lotterielisten von 10 Jahren zu Gebote gestanden, jede von 32 000 bis 34 000 Nummern, wovon ich aber die Nummern über 30 000 in den Listen als nicht vorhanden bei Seite gelassen habe. [Aus diesen 10 Listen wurden mittelst voriger Methode die empirischen Data der obigen Tabellen I und II und hiernach die Bewährungen der Wahrscheinlichkeitsbestimmungen von Q , U und V gewonnen.]
[Es gelte z. B. die Bestimmung von
v für m = 6 . Man hat dann je sechs aufeinander folgende
Nummern der Listen zusammenzunehmen, wobei die Nummern über 30 000
nicht berücksichtigt werden; also, wenn die Nummern 28 904 , 24 460
, 32 305 , 16 019 , 157 , 3708 , 16928 getroffen werden, mit Beiseitelassen
der 3-ten, da sie 30 000 übersteigt, die übrigen sechs nach obiger
Tabelle in Abweichungsgrößen D
umzusetzen, die positiv zu nehmen sind für geradzahlige
Nummern, negativ für ungeradzahlige Nummern. Es stellen somit die
bezeichneten Nummern die Größen + 74 , + 47 , - 26 , - 0,25
, + 5 , + 28 mit dem Mittelwert + 21,3 dar; mithin ist bezüglich des
letzteren µ' = µ,=
3 und v = 0 . Diese Bestimmung, 2000 mal ausgeführt,
ergab die in Tab. I, b unter m = 6 , n = 2000 aufgeführten
Werte.]