U = ![]() =
0,79788 Q log 0,79788 = 0,90194 - 1 (1)
=
0,79788 Q log 0,79788 = 0,90194 - 1 (1)
§ 102. Im allgemeinen findet sich bei K.-G. zwischen der Zahl der positiven und negativen Abweichungen µ ', µ,bez. des arithmetischen Mittels A ein Unterschied u = µ' - µ,, von dem sich fragt, ob er nicht bei wesentlich gleicher W. der beiderseitigen Abweichungen bloß durch unausgeglichene Zufälligkeiten wegen Endlichkeit des m erklärlich ist, oder ob die Mitbeteiligung einer asymmetrischen W. der Abweichungen nach beiden Seiten als mitwirkend anzunehmen ist, da unausgeglichene Zufälligkeiten bei dem endlichen m , mit dem man immer zu tun hat, überhaupt nicht fehlen können, ohne daß sie aber deshalb den gefundenen Unterschied allein zu bedingen brauchen. Hierüber lassen sich Wahrscheinlichkeitsbestimmungen angeben, die zwar aus dem in § 94 angegebenen Grunde für unsere Lehre keine fundamentale Wichtigkeit, aber immerhin ein Interesse haben, was mich veranlaßt, ohne diesen Gegenstand hier erschöpfen und in seiner mathematischen Tiefe verfolgen zu wollen, bis zu gewissen Grenzen darauf einzugehen.
Das Allgemeinste, was sich darüber sagen läßt, ist, daß je größer der Unterschied u dem absoluten Werte nach im Verhältnisse zur Totalzahl m ist, und je größer m selbst ist, desto unwahrscheinlicher wird die Abhängigkeit von bloßen unausgeglichenen Zufälligkeiten, oder, wie wir kurz sagen mögen, die bloße Zufälligkeit des Unterschiedes, um so wahrscheinlicher die Mitabhängigkeit von asymmetrischer W., ohne freilich eine absolute Gewissheit auf diesem Wege überhaupt erreichen zu können. Wohl aber läßt sich angeben, wie groß bei wesentlich symmetrischer W. der zufällige mittlere und wahrscheinliche Unterschied u zwischen µ' und µ,ist, der je nach dem vorhandenem m erwartet werden kann, wenn unter mittlerem Unterschiede, kurz U , der Unterschied verstanden wird, der bei oftmaliger Wiederholung der Beobachtung unter denselben Umständen mit demselben m aus immer neuen Exemplaren desselben Gegenstandes als arithmetisches Mittel der verschiedenen dabei erhaltenen Werte von u (dem absoluten Werte nach) hervorgeht; unter wahrscheinlichem Unterschiede, kurz V , der Wert, der dabei ebenso oft überschritten als unterschritten wird, wovon der erste bezüglich der u-Werte dasselbe, als A bez. der a-Werte, der zweite dasselbe als der Zentralwert bez. der a-Werte ist. In je stärkerem Verhältnisse nun das nach der Wahrscheinlichkeitsrechnung bestimmbare, rein zufällige mittlere und wahrscheinliche u in einer gegebenen Verteilungstafel, resp. U und V , von dem vorgefundenen u überschritten wird, desto unwahrscheinlicher wird die Abhängigkeit desselben von bloßer Zufälligkeit; und es lassen sich selbst nach dem Verhältnisse dieser Überschreitung Grade der Unwahrscheinlichkeit angeben, wofür die Regeln den Mathematikern bekannt sind, worauf ich aber hier nicht näher eingehen will.
Nun scheint es zunächst natürlich, bei der Feststellung der Verhältnisse der u von der bekannten Urne der Wahrscheinlichkeitsrechnung unter der Bedingung auszugehen, daß darin unendlich viele, an Zahl aber gleich viele, weiße und schwarze Kugeln enthalten sind, indem bei Ziehung von je m Kugeln eine gleich große W. für den Zug weißer und schwarzer Kugeln besteht, wonach der Zahlenunterschied u der Kugeln Null sein müßte, nach Zufall aber bei wiederholten, sagen wir n Zügen von je m Kugeln bald die Zahl der einen, bald der anderen Kugeln bald mehr, bald weniger überwiegt, kurz ein zufälliger Unterschied u von zufälliger Größe in zufälliger Richtung erhalten wird. Es läßt sich nicht nur berechnen, sondern auch durch Erfahrung bewähren, wie groß im Falle vieler (streng genommen unendlich vieler) Züge das mittlere und wahrscheinliche u dem absoluten Werte nach sind, und es liegt nahe, das Resultat hiervon, auf den mittleren und wahrscheinlichen Wert des u zu übertragen, was nach bloßem Zufall zwischen der Zahl der positiven und negativen Abweichungen vom arith-metischen Mittelwerte eines K.-G. unter Voraussetzung symmetrischer W. bezüglich desselben erhalten wird. Nun wird allerdings weiterhin (§ 109) ein Umstand angegeben werden, welcher die reine Übertragung des Resultates vom einen auf den anderen Fall untunlich macht; aber gehen wir doch von dem eben besprochenen Falle aus, wobei sich einige interessante, wenn ich nicht irre, bisher unbekannte Verhältnisse herausstellen werden, um erst später auf den verwickelteren, welchen die Kollektivabweichungen darbieten, überzugehen; kurz be-sprechen wir zunächst das Resultat des Zuges der Kugeln aus der Urne unter den angegebenen Verhältnissen, wobei ich mich in betreff der Resultate für größeres m auf Sätze stütze, die ich in den "Recherches sur la probabilité des jugements" von POISSON und den Abhandlungen von HAUBER im 7., 8. und 9. Bande der Zeitschrift für Physik und Mathematik von BAUMGARTNER und ETTINGSHAUSEN finde, und die unstreitig auch anderwärts 1) zu finden sind, indes ich für kleineres m , wofür meines Wissens nach keine Untersuchung vorliegt, auf eigener Untersuchung fuße.
U = ![]() =
0,79788 Q log 0,79788 = 0,90194 - 1 (1)
=
0,79788 Q log 0,79788 = 0,90194 - 1 (1)
V = 0,84535 U log 0,84535 = 0,92703 - 1 (3)
1) daß Q2 = m
2) daß U ganz gleich für ein gegebenes ungerades und das um 1 größere gerade m , also für m = 1 und 2, 3 und 4, 99 und 100 u.s.f. ist.
§ 104. Folgendes die Weise, wie mathematischerseits auf vorige Sätze zu kommen.
Seien jedesmal m , beispielsweise 4 Kugeln aus
der betreffenden Urne gezogen, so können folgende 5 Fälle eintreten:
| Besondere
Zahl der gezogenen weißen
und schwarzen Kugeln |
|
|
| 4 w. | o schw. | + 4 |
| 3 w. | 1 schw. | + 2 |
| 2 w. | 2 schw. | 0 |
| 1 w. | 3 schw. | - 2 |
| 0 w. | 4 schw. | - 4 |
Allgemein, bei gegebenen m , sind die möglichen u-Werte m + 1, wenn die positiven und negativen u unterschieden werden, hingegen bloß ½m + 1 bei geradem m , ½(m + 1) bei ungeradem m , wenn die u nach absolutem Werte, also positive und negative als gleich gezählt werden. Für jedes nicht zu große m sind die möglichen u nach vorigem Schema leicht empirisch zu finden, und es fragt sich nun, wie oft bei sehr oftmaligen Zügen von m , also diesfalls von 4 Kugeln jedes der möglichen u im Verhältnisse zur Gesamtzahl der möglichen u vorkommt, oder kurz, welche W. jedes u hat. Sei diese W. in gleich anzugebender Weise gefunden. Multipliziert man dann jedes u mit seiner W. und addiert diese Produkte, so hat man darin nach bekanntem Prinzip der Wahrscheinlichkeitsrechnung das genaue mittlere u , was wir U nennen. Zunächst scheint es zwar, daß die Summe jener Produkte noch mit der Summe der W. dividiert werden müßte, um das mittlere u zu erhalten; aber jede einzelne W. stellt sich als ein Bruchwert von 1 dar, und die gesamte Summe dieser Bruchwerte gibt 1, was keine besondere Division nötig macht. Ebenso erhält man das mittlere u2 , was wir Q2 nennen, durch Summierung der Produkte der einzelnen u2 in ihre respektive W.
Es gilt also, um U und Q² für ein gegebenes m zu finden, die dabei möglichen u im Sinne obigen Beispieles zu verzeichnen, die W. eines jeden wie folgt zu bestimmen, und dann die Summe der Produkte wie angegeben zu nehmen.
Um nun die W. eines u , kurz W [u] oder W [µ' - µ,], unter Sonderung der positiven und negativen Werte für gegebenes m zu erlangen, hat man folgende, den Mathematikern bekannte Formel 2):
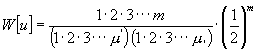 ,
(4)
,
(4)
wobei 1.2.3 ... m das Produkt aller
ganzen Zahlen von 1, an bis inkl. M bedeutet, entsprechend mit µ¢
und µ,, in dem
Falle aber, daß µ¢ oder
µ,= 0 ist, der Wert 1.2.3...
µ' oder 1.2.3... µ ,gleich
1 zu setzen ist.
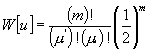
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nehmen wir nun u nach absolutem
Werte rücksichtslos auf sein Vorzeichen, wie wir zu tun haben, weil
U als Mittel aus den absoluten Werten gefaßt wird, so verdoppelt,
sich bei ungeradem m die W. für jedes, u , bei geradem
m , wie es bei m = 4 ist, für jedes u mit. Ausnahme
von u = 0 , und haben wir das vorige Beispiel so zu schreiben:
| ± u | W[± u] |
| 4 | |
| 2 | |
| 0 |
Die entsprechende Durchführung für das ungerade m = 5 und um 1 größere gerade m = 6 gibt:
für m = 5
| ± u | W[±u] |
| 5 | |
| 3 |
|
| 1 |
für m = 6
| ± u | W[± u] |
| 6 | |
| 4 | |
| 2 |
|
| 0 |
[Daraus folgt aber U = 1½ , Q² = 4 für m = 4 ; U = 17/8 , Q2 = 5 für m = 5 und U = 17/8 , Q² = 6 für m = 6 , so daß sich die obigen Sätze bestätigt finden, indem Q² = m für m = 4, 5 und 6, und U für m = 5 und 6 den nämlichen Wert erhält. In gleicher Weise kann für beliebige andere m durch direkte Rechnung eine Bestätigung erzielt werden.]
[Um jedoch die beiden Sätze in ihrer allgemeinen Gültigkeit zu beweisen, bezeichne man Q und U rücksichtlich der Abhängigkeit von m durch Qm und Um , und setze zunächst:
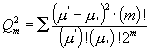 , (5)
, (5)
wo die Summation über alle Wertenpaare ( µ' , µ,) = ( m , 0 ); ( m - 1,1 ); ×××× (1, m - 1); (0, m ) auszudehnen ist, für welche µ' + µ,= m . Somit ist (µ' - µ,)² = (µ¢ + µ,)²-4µ¢ µ, = m² - 4µ'µ,, und man erhält durch Substitution des letzteren Wertes:
![]()
![]() , (6)
, (6)
Da
![]() ,
,
wenn µ¢ = 0 oder µ,= 0, so ist die zweite Summe bloß noch über die Wertpaare (µ¢, µ,) = (m 1, 1), (m 2, 2 ),× × × (1, m 1) zu erstrecken, und man kann darum Qm2 in folgender Form darstellen:
![]() .
(7)
.
(7)
Es ist aber die erste Summe gleich (1 + 1)m : 2m , die zweite gleich (1 + 1)m-2 : 2m-2 , wie unmittelbar zu erkennen, wenn die Dividenden nach dem binomischen Satze entwickelt werden, und der Wert jeder der beiden Summen ist gleich Eins. Daher erhält man:
![]() (8)
(8)
für das um 1 kleinere ungerade m = 2µ - 1:
![]() (9)
(9)
und erstrecke erstenfalls die Summation über die Wertpaare: (µ¢, µ,) = (2µ, 0), (2µ - 1, 1), ××××× (µ + 1, µ - 1); zweitenfalls über die Wertpaare (µ¢, µ,) = (2µ - 1, 0), (2µ - 2, 1),××××× (µ , µ - 1). Man kann nun im ersteren Falle µ¢ = µ + 1 + l , µ,= µ - 1 - l , im letzteren Falle µ¢ = µ + l , µ,= µ - 1 - l , setzen, wo beidesfalls l die µ Werte µ - 1, µ - 2, ×××× 0 anzunehmen hat, so daß man folgende Darstellungsformen gewinnt:
![]()
![]() ; (10)
; (10)
![]() , (12)
, (12)
so ist auch:
![]()
![]() (13)
(13)
und man erhält durch einfache Reduktion:
§ 105. In den beiden vorigen
Sätzen ist nichts über die Zahlenbeziehung enthalten, welche
in den Formeln (1), (2), (3) auf Grund der Anwendbarkeit des G. G. auf
die Wahrscheinlichkeitsverhältnisse der u zwischen den Werten
U , Q und V aufgestellt sind, und liegt im Bisherigen noch
keine [einfache] Abhängigkeit der Werte U und V von
der Größe des m vor, wie wir eine solche doch brauchen.
Substituieren wir nun aber in die obigen Formeln auf Grund von Satz 1)
den Wert ![]() für Q , so erhalten wir folgende zwei Formeln, welche
das Verlangte leisten 4):
für Q , so erhalten wir folgende zwei Formeln, welche
das Verlangte leisten 4):
V = 0,67449![]() , (15)
, (15)
![]()
für l = 1, 2,... µ - 1 durch
![]()
ersetzt.]
Vergleich der genauen Werte von U mit den nach (16) berechneten.
| m | genau | 0,797 88 |
diff. |
| 1 u. 2 |
|
|
- 0,0228 |
| 3 u. 4 |
|
|
- 0,0073 |
| 5 u. 6 |
|
|
- 0,0038 |
| 7 u. 8 |
|
|
- 0,0024 |
| 9 u. 10 |
|
|
- 0,0017 |
| 11 u.12 |
|
|
- 0,0012 |
| 15 u.16 |
|
|
- 0,0008 |
| 25 u.26 |
|
|
- 0,0004 |
Wie man sieht, weichen alle nach Formel (16) berechneten Werte von U in minus von den genauen ab, aber selbst bei m = 1 und 2 ist die Abweichung sehr unbedeutend, beträgt bei m = 25 und 26 nur noch 4 Einheiten der 4. Dezimale und nimmt mit Vergrößerung des m weiter ab. Natürlich gibt die unkorrigierte Formel (14) bei kleinem m viel größere Abweichungen von dem genauen Werte; bei m = 25 beträgt sie noch - 0,0401, bei m = 26 noch + 0,0389; und nur bei viel größerem m wird sie nach Formel (14) wie nach Formel (16) merklich verschwindend.
§ 106. Was den Wert V anlangt, so würde derselbe prinzipiell genau dadurch gegeben sein, daß man den Wert u bestimmte, bezüglich dessen die Wahrscheinlichkeit größerer u gleich der Wahrscheinlichkeit kleinerer u ; aber versuchen wir dies auf Beispiele mit kleinem m , wie die obigen mit m = 4, 5 oder 6 anzuwenden, so geben dieselben keinen solchen Wert her, sondern welche Werte wir dafür nehmen wollen, so ist die Wahrscheinlichkeitssumme der größeren und kleineren u ungleich, und hätte man denselben, wenn man überhaupt einen bestimmten Wert dafür verlangt, zwischen zweien von den u zu suchen, die um je 2 auseinanderliegen, z. B. bei m = 5 zwischen u = 3 und 1, bei m = 6 zwischen u = 2 und 0, ohne daß, so viel ich sehe, ein rationelles Prinzip für eine genauere Bestimmung vorliegt, was doch nicht hindert, bei einem so großen m , daß ± 2 dagegen verschwindet, die Formel (15) dafür zulässig zu finden. Inzwischen schien mir von Interesse, eine Bestimmung auch für kleinere m nach folgendem Prinzip zu versuchen.
Die Zahl der Werte z , die auf einen Wert a eines K.-G. geschrieben wird, sei es in einer primären oder reduzierten Tafel, ist nach früheren Auseinandersetzungen eigentlich auf ein ganzes Intervall verteilt zu denken, dessen Grenzen bei äquidistanten a in die Mitte zwischen je zwei a fallen. Vergleichen wir nun die äquidistanten u mit den äquidistanten a , so lassen sich nach Analogie die Wahrscheinlichkeiten, die jedem u zukommen, auf ein Intervall von der Größe 2 verteilt denken, und hiernach ganz in derselben Weise, wie wir den Zentralwert der a durch Interpolation des Intervalles, in welches er fällt, finden (s. § 82), so den Zentralwert der u , d. i. V ; durch Interpolation seines Intervalles finden. Ich sage nicht, daß diese Betrachtung streng ist; denn jene Verteilung der z bei K.-G. ist durch die Natur der Sache als notwendig gegeben, hiergegen bei den u an sich durch nichts gefordert, und eine durch Interpolation gefundene Bestimmung nicht mit einer genauen zu verwechseln. Indessen ließ sich doch der Versuch machen, was dabei herauskommt, und ließen sich die so gefundenen Werte für gegebene m mit den für großes m durch Formel (15) gegebenen vergleichen. Anstatt aber bloß Interpolation mit ersten Differenzen habe ich die genauere mit zweiten Differenzen dabei angewandt und folgende Resultate erhalten:
Vergleich der interpolierten V mit den nach (15) berechneten.
|
|
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
| 6 |
|
|
|
| 7 |
|
|
|
| 8 |
|
|
|
| 9 |
|
|
|
| 10 |
|
|
|
| 15 |
|
|
|
| 20 |
|
|
|
| 25 |
|
|
|
Man sieht, daß der Vergleich in der Tat nicht erfolglos ist, indem die durch Interpolation erhaltenen V-Werte selbst bei ganz niederen Werten von m mit denen, welche der Formel (15) entsprechen, fast genau übereinkommen. Und es bleibt nur auffällig, daß die Differenzen zwischen den zusammengehörigen Werten keinen regelmäßigen Gang befolgen, und, während die meisten nach (15) berechneten Werte um eine Kleinigkeit kleiner als die interpolierten Werte sind, bei ein paar (für m = 5 und 10) das Umgekehrte statt findet, was nicht auf Rechenversehen beruht, wie ich mich durch sorgfältige Revision überzeugt habe.
[Gerade diese durchgängige Übereinstimmung
zeigt jedoch, daß die interpolationsmäßige Bestimmung
nur insoweit zutreffend ist, als die Formel (15) den wahrscheinlichen Wert
von u mit hinreichender Annäherung darstellt. Da aber dies
der Herleitung jener Formel zu folge nur dann der Fall ist, wenn Größen
von der Ordnung 1 :![]() vernachlässigt
werden dürfen, so wird man sich für kleinere m weder der
Formel (15), noch des Interpolationsverfahrens mit Vorteil bedienen, vielmehr
lieber an genauere Bestimmungen von V sich halten. Solche lassen
sich in sukzessiver Annäherung an den wahren Wert mittels der Summenformel
von MAC LAURIN, die auch EULER's Summenformel heißt, gewinnen. Es
besteht nämlich die prinzipielle Bedeutung jener Summenformel darin,
daß sie die Berechnung einer diskreten Summe, bei Erfüllung
gewisser Bedingungen, auf Integration und Differentiation zurückführt
und dadurch an Stelle des von Intervall zu Intervall sprungweise sich ändernden
Summenwertes einen stetiger Veränderung fähigen Ausdruck setzt.
Geschieht dies für die Summe der Werte W[± u],
so kann dasjenige u bestimmt werden, bis zu welchem die Summe der
oberhalb und unterhalb gelegenen Werte gleich ½ ist, wodurch eben
V gefunden wird.]
vernachlässigt
werden dürfen, so wird man sich für kleinere m weder der
Formel (15), noch des Interpolationsverfahrens mit Vorteil bedienen, vielmehr
lieber an genauere Bestimmungen von V sich halten. Solche lassen
sich in sukzessiver Annäherung an den wahren Wert mittels der Summenformel
von MAC LAURIN, die auch EULER's Summenformel heißt, gewinnen. Es
besteht nämlich die prinzipielle Bedeutung jener Summenformel darin,
daß sie die Berechnung einer diskreten Summe, bei Erfüllung
gewisser Bedingungen, auf Integration und Differentiation zurückführt
und dadurch an Stelle des von Intervall zu Intervall sprungweise sich ändernden
Summenwertes einen stetiger Veränderung fähigen Ausdruck setzt.
Geschieht dies für die Summe der Werte W[± u],
so kann dasjenige u bestimmt werden, bis zu welchem die Summe der
oberhalb und unterhalb gelegenen Werte gleich ½ ist, wodurch eben
V gefunden wird.]
[Es ergibt sich nun, wie im ersten Zusatz (§ 110) dargelegt wird, für gerade und ungerade m:
V = 0,674 489 ![]() -
1 ; (17)
-
1 ; (17)
wofern Größen von der Ordnung 1 :![]() berücksichtigt,
solche von der Ordnung 1 : m vernachlässigt werden.
Bei Mitnahme der Größen von der Ordnung 1 : m
ferner findet man:
berücksichtigt,
solche von der Ordnung 1 : m vernachlässigt werden.
Bei Mitnahme der Größen von der Ordnung 1 : m
ferner findet man:
![]() ;
(18a)
;
(18a)
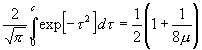 (18c)
(18c)
zu finden ist. Die beiden Formeln (18a), (18b)
bilden das Analogon zu (16); sie haben zur Folge, daß nahehin die
V für ein gerades m und und das nächst folgende
ungerade einander gleich sind und völlig gleich würden, wenn
c![]() mit
Vernachlässigung des Gliedes 1 : 16µ in (18c)
gleich 0,67449 gesetzt würde.]
mit
Vernachlässigung des Gliedes 1 : 16µ in (18c)
gleich 0,67449 gesetzt würde.]
[Zum Vergleiche der drei Näherungsformeln (15), (17) und (18), deren V der Reihe nach als V1 , V2 und V3 bezeichnet werden, dient folgende Zusammenstellung:
|
|
|
|
|
| 4 | 1,349 | 0,349 | 0,565 |
| 5 | 1,508 | 0,508 | 0,529 |
| 6 | 1,652 | 0,652 | 0,827 |
| 9 | 2,023 | 1,023 | 1,043 |
| 10 | 2,133 | 1,133 | 1,267 |
| 11 | 2,237 | 1,237 | 1,257 |
| 20 | 3,016 | 2,016 | 2,111 |
| 100 | 6,745 | 5,745 | 5,786 |
| 1000 | 21,329 | 20,329 | 20,333 |
§ 107. Da abgesehen von den interpolationsmäßig herzustellenden V alle vorigen Bestimmungen auf zweifelsfreien arithmetischen Prinzipien und Sätzen beruhen, so dürfte eine empirische Bewährung derselben an sich nicht nötig sein, indes will ich doch auf eine solche eingehen, teils weil die Methode der Bewährung an sich ein eigentümliches Interesse durch den Ersatz der Wahrscheinlichkeitsurne darbieten dürfte, teils weil ihre Resultate einen gewissen Anhalt geben, in wie weit man die genauen Werte von Q und U für gegebenes m , welche prinzipiell eine Bestimmung aus unendlichem n voraussetzen, bei großem, doch immer noch endlichem n , wie es empirisch zu Gebote steht, wiederzufinden erwarten kann.
Unstreitig gewährt die Urne mit unendlich vielen, an Zahl gleichen weißen und schwarzen Kugeln eine sehr geeignete Vorstellung, an welcher man die vorigen Sätze erläutern kann, aber eine solche Urne läßt sich nicht herstellen, und auch, wenn man sie durch eine Urne mit einer endlichen Zahl von Kugeln ersetzt, in die man die m Kugeln nach jedem Zuge zurücktut, was wohl geschehen kann, würde das Verfahren bei sehr vielen Zügen außerordentlich langweilig und die Herstellung einer ganz zufälligen Mischung der Kugeln vor jedem neuen Zuge schwerlich erreichbar sein, kurz die wirkliche Anwendung des Verfahrens immer praktisch undurchführbar sein; auch wüßte ich nicht, daß je Gebrauch davon gemacht worden. Aber es steht das Äquivalent der Urne in den Listen gezogener Gewinnummern der Lotterie zu Gebote, von welchen die geradzahligen als weiße, die ungeradzahligen als schwarze Kugeln, oder bei Vergleich mit positiven und negativen Abweichungen von gleicher W., die einen als positiv, die anderen als negativ gefaßt werden können.
Hierzu habe ich mir (in den 50er Jahren) von den betreffenden Behörden die Listen von zehn sächsischen Lotterien von 1843 bis mit 1852 mit je 32000 bis 34000 Nummern ver-schafft, Listen, in welchen die Gewinnummern nach der zufälligen Folge, in der sie gezogen wurden, stehen, als wie 28904; 24460; 32305; 16019; 157; 3708; 16 928 u.s.w. Obwohl nun die Anzahl der Nummern jeder Jahreslotterie immer nur eine endliche Zahl bleibt, und die gezogenen Nummern nicht in das Glücksrad zurückgelegt werden, so ändert doch die Ziehung der früheren Nummern nichts in dem Wahrscheinlichkeitsverhältnis der späteren, wie es bei der Anwendung der Urne mit einer endlichen Zahl Kugeln der Fall sein würde, und kann man es so ansehen, als wenn eine Urne mit einer unendlichen Zahl Kugeln vorläge5).
5 ) Die Losnummern im Glücksrade
stellen sich, soviel ich bei einem deshalb vorgenommenen Besuche der Anstalt
habe beobachten können, als kleine Stifte dar, welche, näher
besehen, kleine Röllchen sind, bestehend aus fest zusammengerollten
und durch ringförmige Hülsen gesteckten Zetteln, auf welchen
die Nummern enthalten sind. Vielleicht ist diese Beschreibung nach der
Erinnerung nicht ganz genau, worauf aber hier nichts an-kommt. Vor der
Ziehung sind diese Nummern auf Brettern nach ihrer Reihenfolge geordnet,
je 1000 auf einem Brett. Diese Bretter werden in unregelmäßiger,
durch zufälligen Aufruf eines Beamten bestimmten Reihenfolge erst
in einen Kasten und von hier aus in das Glücksrad entleert, so daß
von vornherein eine unregelmäßige Mischung nach Tausenden statt
hat, dann das Rad umgedreht, und dies nach je 100 gezogenen Nummern wiederholt.
An der Achse des Rades sind vier durchbrochene Flügel angebracht,
welche sich in entgegengesetzter Richtung des Rades drehen und dadurch
die unregelmäßige Mengung befördern. Sieht man zu, wie
dies geschieht, und die Lose durcheinander fallen, so fühlt man sich
versucht, zu glauben, dass schon ganz wenige Drehungen hinreichen, die
Mischung ganz unregelmäßig zu machen; doch sollen nach Aussage
der Beamten bei den ersten Ziehungen, in welche die Lotterie eingeteilt
ist, noch öfter Nachbarzahlen nacheinander erscheinen, indes bei der
letzten Ziehung, nachdem die Mengung durch mehrhundertmalige Drehung des
Rades bewirkt ist, nichts mehr der Art bemerkt wird.
Erläutern wir die Anwendung hiervon zunächst an dem einfachen Fall von m = 3, wo bloß die beiden ± u = 1 und 3 mit der theoretischen W[u] = 0,75 respektive 0,25 möglich sind, welche sich nach angegebenen Regeln finden lassen. Bei 2000maliger Wiederholung der Bestimmung von m = 3 aus immer neuen Nummern, also n = 2000, wurden im ganzen folgende Resultate erhalten:
Empirische Zahl, wie oft ein ± u in n Serien von je m = 3 Werten vorkam, verglichen mit der theoretischen Zahl
| ±u | theoretisch | Empirisch |
| 1 | 1500 | 1494 |
| 3 | 500 | 506 |
Dividiert man die erhaltenen Zahlen mit n , so erhält man aus voriger Tabelle folgende Bestimmungen:
| ±u | theoretisch | Empirisch |
| 1 | 0,750 | 0,747 |
| 3 | 0,250 | 0,253 |
woraus sich dann Q² , U , V , wie früher angegeben, bestimmen lassen; also z. B. theoretisch Q² = 1 × 0,750 + 9 × 0,250 = 3; und U = 1 × 0,750 + 3 × 0,250 = 1,5. Entsprechend sind die folgenden Resultate mit größerem m und verschiedenem, nur immer sehr großem n zu verstehen und zu behandeln.
Empirische Zahl, wie oft ein ± u in n Serien von je m Werten vorkam, verglichen mit der theoretischen Zahl.
| ± u |
|
|
|
|||
|
|
theoretisch | Empirisch | theoretisch | Empirisch | theoretisch | empirisch |
| 0 | 1230 | 1201 | 112 | 110 | 48 | 46 |
| 2 | 2051 | 2027 | 216 | 217 | 93,5 | 104 |
| 4 | 1172 | 1225 | 192 | 194 | 88 | 85 |
| 6 | 439 | 442 | 158 | 154 | 80 | 67 |
| 8 | 98 | 97 | 119,5 | 120 | 69,5 | 68 |
| 10 | 10 | 8 | 84 | 65 | 58 | 63 |
| 12 | | | 54 | 62 | 47 | 51 |
| 14 | | | 32 | 41 | 36 | 31 |
| 16 | | | 17 | 21 | 27 | 34 |
| 18 | | | 9 | 10 | 19 | 13 |
| 20 | | | 4 | 3 | 13 | 14 |
| 22 | | | 2 | 2 | 8,5 | 8 |
| 24 | | | 0,5 | 1 | 5,5 | 7 |
| 26 | | | | | 3 | 4 |
| 28 | | | | | 2 | 2 |
| 30 | | | | | 1 | 1 |
| 32 | | | | | 0,5 | 0 |
| 34 | | | | | 0,3 | 1 |
| 36 | | | | | 0,1 | 1 |
| 38 | | | | | 0,1 | 0 |
|
|
5000 | 5000 | 1000 | 1000 | 600 | 600 |
Die möglichen Werte u in voriger Tabelle sind für m = 50 und 100 nicht bis zu Ende durchgeführt, die noch fehlenden aber von merklich verschwindender W., so daß ein ungeheures n nötig gewesen sein würde, sollten solche ein oder das andere Mal vorkommen.
Aus voriger Tabelle ist folgende Tabelle
der empirischen Q² , U , V im Vergleich mit den theoretischen
Werten abgeleitet.
|
m |
n |
|
|
|
|||
| theoretisch | empirisch | theoretisch | empirisch | 0,674 49 |
empirisch interpol. | ||
| 3 | 2000 | 3,00 | 3,02 | 1,50 | 1,51 | 1,17 | 1,18 |
| 10 | 5000 | 10,00 | 10,13 | 2,46 | 2,49 | 2,13 | 2,19 |
| 50 | 1000 | 50,00 | 52,02 | 5,61 | 5,71 | 4,77 | 4,76 |
| 100 | 600 | 100,00 | 101,68 | 7,96 | 8,05 | 6,74 | 6,94 |
Die nahe Übereinstimmung der empirischen Werte mit den theoretischen ist unstreitig befriedigend und nur auffällig, daß bei allen Werten von m sich das empirische Q² und U ein wenig größer als das theoretische findet, was wohl nur deshalb der Fall ist, weil die Serien für die größeren m größtenteils durch Zusammenlegen der Serien, welche für die kleineren m erhalten worden waren, erhalten wurden, so daß diese ihren Einfluß auf erstere mit erstrecken konnten, was wegen der Quadrierung des u bei Bestimmung von Q2 merklicher werden mußte als bei U , wo sich das Entsprechende in geringerem Grade zeigt.
§ 108. Die vorigen Betrachtungen und Formeln können vielfach von nützlicher Anwendung bei statistischen Untersuchungen sein. Z. B. es gelte zu untersuchen, ob der Unterschied, der zwischen der Zahl der Geburten oder Todesfälle oder Selbstmorde in zwei verschiedenen Jahreszeiten, oder zwischen der Zahl der männlichen und weiblichen Geburten, oder zwischen der Zahl der Gewitter an zwei verschiedenen Lokalitäten besteht, rein zufällig ist, oder ob die Beschaffenheit der Jahreszeiten, des Geschlechtes, der Lokalität einen wesentlichen Einfluß auf die Größe und Richtung des Unterschiedes hat. Sei in Summa für beide unterschiedenen Bedingungen eine sehr große Zahl, sagen wir m , Fälle beobachtet worden und hierbei gefunden, daß auf die eine Seite µ' , auf die andere µ,Fälle kommen, mithin der absolute Unterschied u ist, so wird es darauf ankommen, ob der gefundene Unterschied u im absoluten Werte den wahrscheinlichen V übersteigt oder untersteigt, und in welchem Verhältnisse dies der Fall ist, um Wahrscheinlichkeitsschlüsse folgender Art zu machen.
Wäre die W. von µ' und µ,gleich, mithin der gefundene Unterschied u rein zufällig, so würde es eben so wahrscheinlich sein, daß er den für diese Voraussetzung symmetrischer W. nach vorigen Formeln bestimmten, wahrscheinlichen Unterschied V überstiege und unterstiege, und wenn die Beobachtung mit demselben m sehr oft wiederholt würde, würde er im Mittel mit V merklich gleich gefunden werden; hiergegen wird ein bloß zufälliger Unterschied natürlich um so unwahrscheinlicher, in je größerem Verhältnisse er den unter Voraussetzung bloßer Zufälligkeit bestimmten wahrscheinlichen V übersteigt; hieraus die W., daß er nicht bloß zufällig sei, um so größer, in je größerem Verhältnisse dieses Übersteigen stattfindet; und sofern die Verhältnisse rein zufälliger u bei großem m mit den Verhältnissen der Beobachtungsfehler nach G. G. zusammenstimmen, werden auch nach einer Tabelle des G. G., welche die Wahrscheinlichkeitsverhältnisse der Fehler als Funktion des Verhältnisses gibt, in dem der wahrscheinliche Fehler w von ihnen überstiegen oder unterstiegen wird, sich unter Substitution von V für w noch bestimmtere Wahrscheinlichkeitsrechnungen in vorigen Beziehungen anstellen lassen.
Gegen diese allgemeinen Sätze dürfte sich meines Erachtens kein haltbarer Einwand erheben lassen; in betreff der bestimmten Auslegung aber, die ich folgends den Verhältnissen u : V im Interesse ihrer praktischen Verwertung gebe, dürfte bei der großen Leichtigkeit von Fehlbegriffen und Fehlschlüssen in diesem Felde die prinzipielle Revision seitens eines mit der Wahrscheinlichkeitsrechnung vollkommen vertrauten Fachmathematikers wohl noch erwünscht sein.
Seien beispielsweise m = 1000 Gewitter während derselben Zeitperiode an zwei Orten, für beide zusammengenommen, beobachtet, am einen µ' = 530 , am anderen µ,= 470 , also u = 60 ; so ist, nach Formel (15), der wahrscheinliche Unterschied V , den wir nach bloßem Zufalle erwarten und, unter der gleichen Voraussetzung symmetrischer W. für u und D , für das w der Fehlertabelle einsetzen können:
Lassen wir diese Betrachtungsweise gelten und gehen damit auf die vorigen Beispiele zurück, so findet sich erstenfalls, wo der gefundene Unterschied u = 60 und V = 21,33, mithin u : V = 2,81 ist, nach der Tabelle des G. G., daß die W., der Unterschied u werde als rein zufällig unter diesem Werte bleiben, sich zur W. des Gegenteils wie 0,942 gegen 0,058 verhält; und sofern jener Wert u doch erreicht ist, wird man in runder Zahl 94 gegen 6 wetten können, er sei nicht bloß zufällig. Im zweiten Falle, wo u =10 = 0,47 V , findet sich nach der betreffenden Tabelle, daß die W., der Unterschied u werde als zufälliger unter diesem Werte bleiben, sich zum Gegenteil wie 0,249 zu 0,751 verhält, sofern er aber nicht unter diesem Werte geblieben ist, findet die entgegengesetzte W. dafür statt, daß er als zufälliger diesen Wert erreicht hat, und wird man in runder Zahl nur 1 gegen 3 wetten können, daß ein lokaler Einfluß den zufälligen überboten habe, 3 gegen 1 aber für das Gegenteil, ohne doch wetten zu können, daß ein lokaler Einfluß überhaupt nicht vorhanden gewesen sei. Ich wüßte wenigstens nicht, wie diese Verhältnisse anders zugleich praktisch und rationell zu fassen seien.
Sei Ww die W.,
daß D oder u unter Voraussetzung
symmetrischer W. unter einem gegebenen Bruchteile oder Multiplum von w
oder V bleiben werden, so hat man, um einen kleinen Auszug aus
der hierher gehörigen Tabelle 6) des
G. G. zu geben, zu einander gehörig:
| u | Ww | u | Ww | |
| 0,10 V | 0,05378 | 2,25 V | 0,87088 | |
| 0,25 V | 0,13391 | 2,50 V | 0,90825 | |
| 0,50 V | 0,26407 | 2,75 V | 0,93638 | |
| 0,75 V | 0,38705 | 3,00 V | 0,95698 | |
| 1,00 V | 0,50000 | 3,25 V | 0,97163 | |
| 1,25 V | 0,60083 | 3,50 V | 0,98176 | |
| 1,50 V | 0,68833 | 4,00 V | 0,99302 | |
| 1,75 V | 0,76214 | 4,50 V | 0,99760 | |
| 2,00 V | 0,82266 | 5,00 V | 0,99926 |
Man hat sich aber bei Anwendung voriger
Bestimmung vor einer fehlerhaften Anwendung derselben in folgendem Sinne
zu hüten. Gesetzt man hat, sei es irgend zwei Monate oder irgend zwei
Jahreszeiten, ohne die übrigen, in betreff der Anzahl von Gewittern
in Untersuchung genommen, so wird nichts hindern, die vorige Bestimmung
in betreff der Frage, ob der Unterschied der beiden Monate oder Jahreszeiten
einen anderen als bloß zufälligen Einfluß auf die Zahl
der Gewitter habe, eben so in Anwendung zu bringen, als wenn es sich um
den lokalen Einfluß der Örtlichkeit handelt. Aber gesetzt, man
habe die Beobachtung der Gewitterzahl mit gegebenem m für alle
12 Monate vorgenommen, so wird, auch wenn für alle Monate dieselbe
W. der Gewitterzahl besteht, das u bei Vergleich je zweier derselben
nach Zufall verschieden ausfallen, und es werden sich darunter zwei Monate
finden lassen, die das größte u geben, was leicht so
groß sein könnte, daß nach seinem Verhältnisse zu
V auf überwiegende W. eines wesentlichen Einflusses zu schließen.
Aber dieser Schluß würde in sofern irrig sein, als unter einer
größeren Anzahl von Fällen auch bei geringer W. doch große
Abweichungsunterschiede auftreten können. Jedenfalls bleiben dann
die betreffenden Monate wegen eines spezifischen Einflusses verdächtig;
zur Sicherstellung aber müßte meines Erachtens an ihnen die
Beobachtung noch besonders erweitert und z. B. bis zur doppelten Zahl fortgesetzt
werden, um zu sehen, ob sich der Wahrscheinlichkeitsschluß bestätigt
7).
6 ) [Diese Tabelle findet man im Berliner Astronom. Jahrbuch für 1834, S. 309 flgd.]
7 ) [Vergl. zu diesem Paragraphen den
zweiten Zusatz (§ 111).]
§ 109. Zunächst scheint nun, daß von vorigen Betrachtungen und Formeln auch unmittelbare Anwendung auf die Aufgabe zu machen, aus der Größe des Unterschiedes u , der zwischen der Zahl der positiven und negativen Abweichungen + D und - D bez. des arithmetischen Mittels A besteht, nach W. zu schließen, ob der Unterschied bloß von Zufälligkeiten abhängen könne, oder ob in der Natur des Gegenstandes und seiner Existenzbedingungen ein Einfluß begründet liegt, der am Übergewicht der Zahl der einen oder anderen Abweichungen wenn schon nicht alleinige doch Mitschuld trägt, oder kurz, ob wesentliche Asymmetrie an dem Unterschiede Anteil hat. Und in der Tat, wenn wir von vornherein versichert wären, daß die Abweichungen der Exemplare a von ihrem arithmetischen Mittel A dieselbe symmetrische W. nach beiden Seiten zeigen, als die weißen und schwarzen Kugeln bei Ziehung derselben, so würden die vorigen Betrachtungen und Formeln ganz darauf anwendbar sein; aber das ist nach folgenden Betrachtungen nicht der Fall.
Nennen wir im Sinne eines bekannten
Sprachgebrauches wahres Mittel A¥das
Mittel aus einer unendlichen Zahl von Exemplaren, falsches Mittel Am
das uns nur zu Gebote stehende aus einer
endlichen Zahl m . Setzen wir nun symmetrische W. der Abweichungen
bez. des wahren Mittels voraus, so werden doch sowohl die beiderseitigen
Abweichungssummen, als die beiderseitigen Abweichungszahlen bez. desselben
nach Zufall ungleich sein und sich normaler Weise bei Änderung der
Gesamtzahl m der Abweichungen zwar nicht einander proportional,
aber in funktionalem Zusammenhange nach gleicher Richtung, d. h. in Zunahme
oder Abnahme ändern 8). Wird nun aus
einer endlichen Zahl von a das falsche Mittel gezogen, so verschwindet
damit der Unterschied zwischen den beiderseitigen Abweichungssummen, da
das ja im Wesen des arithmetischen Mittels liegt; man macht dabei die Summen
so zu sagen künstlich gleich, und wenn sich Summen und Zahlen einander
proportional änderten, so würde mit dem Unterschiede zwischen
den beiderseitigen Summen zugleich der Unterschied u zwischen den
beiderseitigen Zahlen verschwinden, was nicht nur erfahrungsmäßig
nicht der Fall ist, sondern auch wegen nicht proportionaler Änderung
nicht zu erwarten ist. Aber jedenfalls mindert sich mit Aufhebung des Unterschiedes
zwischen den beiderseitigen Abweichungssummen der funktional damit zusammenhängende
Unterschied zwischen den beiderseitigen Zahlen gegen den Fall, daß
die Abweichungen vom wahren Mittel genommen wurden, für welchen die
obigen Formeln gelten, und läßt sich also voraussehen, daß
der mittlere und wahrscheinliche Wert von u bez. des falschen Mittels,
von dem wir sie doch nur rechnen können, bei gleichem m geringer
ausfallen müssen, als bez. des wahren, und daß obige Formeln
also nicht mehr dafür maßgebend sein können.
8 ) Man berücksichtige, daß,
während das wahre Mittel immer aus einer unendlichen Zahl von a
gezogen zu denken ist, doch die Zahl m der genommenen Abweichungen
eine mehr oder weniger große endliche sein kann.
Inzwischen lassen sich doch aus Vorigem zunächst folgende zwei Folgerungen ziehen: 1) die W. eines wesentlichen Einflusses ist bei Anwendung der obigen Formeln auf den Abweichungsunterschied u bez. des arithmetischen Mittels Am bei gegebenem m für noch größer anzunehmen, als es nach obigen Formeln erscheint, weil V , im Verhältnisse zu welchem u in Betracht kommt, bezüglich Am jedenfalls kleiner als bez. A¥ ist, wofür die obigen Formeln gelten.
2) Lassen wir bez. des falschen Mittels Am ebenso wie bez. des wahren A¥ die Voraussetzung symmetrischer W. gelten, nennen aber dann die oben bezüglich des ersteren mit u , Q , U , V bezeichneten Werte, wenn sie vielmehr bez. des letzteren bestimmt werden resp. V, Q, U, V, so wird es nur gelten, diese entsprechend als Funktion des m bez. Am zu bestimmen, als jene in Bezug auf A¥ bestimmt wurden, um damit Formeln zu erlangen, welche zu entsprechendem Gebrauche dienen können.
§ 110. [Erster Zusatz. Bestimmung des wahrscheinlichen Unterschiedes V mittelst der Summenformel von MAC LAURIN oder von EULER:]
[Diese Summenformel lautet 9):
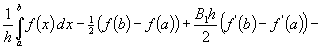
wo b = a + nh und B1 = 1/6 ; B3 = 1/30 × × × × die BERNOULLI'schen Zahlen sind.]
[Um nun die W[± u] nach dieser Formel zu summieren, ist nicht die ursprüngliche Form (4), sondern die hieraus auf Grund der Näherungsformel:
![]() , (20)
, (20)
oder, wenn man Glieder von der Ordnung 1 : n berücksichtigt, auf Grund der korrigierten Formel:
[Benutzt man zunächst (20), so ist für m = 2µ ; µ¢ = µ + v ; µ,= µ - v ; u = 2v :
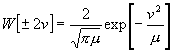 ;
; ![]() . (22)
. (22)
Die Summe der W [u] zwischen den Grenzen + 2 n und - 2 n , oder die Summe der W [± u] zwischen den Grenzen 0 und 2 n wird somit gegeben durch:
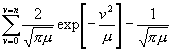 .
(23)
.
(23)
Nun ist aber nach (19), wenn im Einklänge mit der durch (20) gegebenen Annäherung Glieder von der Ordnung 1 : µ vernachlässigt werden:
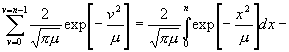
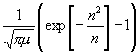 .
(24)
.
(24)
Folglich erhält man:
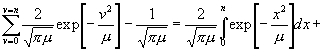
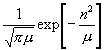 .
(25)
.
(25)![]() ;
oder
;
oder ![]()
die Bestimmung:
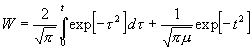 . (26)
. (26)
9 ) [EULER leitet sie ab in den Institutiones
calculi differentialis, Pars post., Cap.V. Reprod. z. B. in SCHLÖMILCH's
Kompendium der höheren Analysis, zweiter Band, S. 226.]
Ihr zufolge wird der wahrscheinliche Wert von u , d. i. V , gegeben durch:
![]() ,
(27)
,
(27)
wenn t der Bedingung:
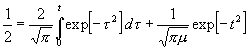 (27a)
(27a)
genügt. Denn es ist alsdann die W., daß
± u < 2t![]() gleich ½ . Um hieraus t zu berechnen, setze man t
= c + g, und bestimme c aus
gleich ½ . Um hieraus t zu berechnen, setze man t
= c + g, und bestimme c aus
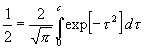 ,
,
so daß es sich der t-Tabelle zufolge gleich 0,476 936 findet; dann zerlegt sich das Integral zwischen den Grenzen 0 und c + g in zwei Integrale zwischen den Grenzen 0 und c und zwischen den Grenzen c und c + g, und es resultiert:
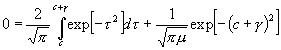 .
.
Da aber geine Größe
von der Ordnung 1 :![]() ist, so erhält man eine genügende Genauigkeit, wenn exp [- t2]
in Erstreckung des Integrals konstant gehalten und gleich exp [- (c
+ g )2] gesetzt
wird. Es wird somit, nach Division mit exp [- (c + g
)2]:
ist, so erhält man eine genügende Genauigkeit, wenn exp [- t2]
in Erstreckung des Integrals konstant gehalten und gleich exp [- (c
+ g )2] gesetzt
wird. Es wird somit, nach Division mit exp [- (c + g
)2]:
![]() oder
oder ![]() .
.
Auf Grund dessen erhält man10):
![]() .
(28)
.
(28)
Da anfänglich m = 2µ gesetzt
wurde, so könnte es scheinen, daß diese Formel nur für
geradzahlige m gelte. Indessen ergibt sich für m = 2µ
- 1 das nämliche Resultat, wie nicht anders zu erwarten ist, da
nur Größen von der Ordnung 1 :![]() berücksichtigt werden.]
berücksichtigt werden.]
10 ) [Eben diese Formel gibt auch MEYER
in den Vorlesungen über Wahrscheinlichkeitsrechnung bei der Behandlung
des BERNOULLI'schen Theorems, S.107.]
[Will man aber Größen von der Ordnung 1 : m berücksichtigen, so muß man statt (20) die Näherungsformel (21) benutzen und den Fall, daß m geradzahlig, von dem Falle, daß m ungeradzahlig ist, scheiden.]
[Erstenfalls ist von (22) auszugehen, nachdem den dortigen Bestimmungen der Faktor (1 - 1 : 8µ) beigefügt ist. Man findet alsdann mittelst (19) unter Mitnahme der ersten Ableitungen:
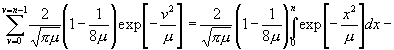
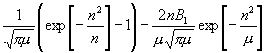 , (29)
, (29)![]() oder
oder ![]() ,
,
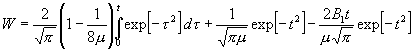 .
(30)
.
(30)
Um hieraus V zu gewinnen, ist W = ½ anzunehmen, sodann t aus der Gleichung:
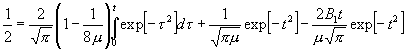 (31)
(31)
zu berechnen und
![]()
![]() (31a)
(31a)
zu setzen. Man nehme nun wie oben t = c + g an, bestimme c der Art, daß nach Division der Gleichung (31) mit (1 1 : 8µ) oder, was dasselbe ist, nach Multiplikation mit (1 +1 : 8µ)
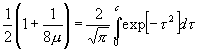 , (32)
, (32)
und finde g aus:
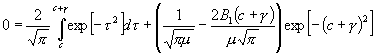 . (33)
. (33)
Diese Gleichung nimmt mit Rücksicht, daß g
eine kleine Größe von der Ordnung l : ![]() ist, nach Division mit exp[ - (c + g
)2] die einfache Form:
ist, nach Division mit exp[ - (c + g
)2] die einfache Form:
![]() oder
oder ![]() (33a)
(33a)
an, woraus, da B1 = 1 : 6 und 2µ = m , als wahrscheinlicher Wert für geradzahlige m :
![]() (34)
(34)
folgt.]
[Ist m ungerade = 2µ
- 1 , so ist, wenn µ' = µ + v ;
µ,= µ - v
1 ; u = 2v + 1 :
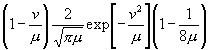 , (35)
, (35)
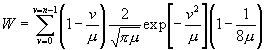 . (36)
. (36)
Somit besteht auf Grund von (19), wenn n = t![]() , die Wahrscheinlichkeit:
, die Wahrscheinlichkeit:
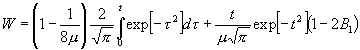 (37)
(37)
dafür, daß
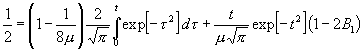 , (38)
, (38)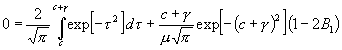 (39)
(39)![]() , (39a)
, (39a)
folglich
![]()
und schließlich:
![]() ,
,
woraus mit Rücksicht auf m = 2µ - 1 als wahrscheinlicher Wert für ungerade m
![]() (40)
(40)
sich ergibt]
§ 111. [Zweiter Zusatz. Den Erörterungen des § 108 liegt das Problem zu Grunde, aus einer großen Zahl beobachteter Fälle unbekannte Wahrscheinlichkeiten zu ermitteln. Dasselbe steht zu der Umkehrung des BERNOULLl'schen Theorems in Beziehung, wonach für die unbekannte W. Grenzwerte angegeben werden können und zugleich der Wahrscheinlichkeitsgrad berechnet werden kann, mit dem die unbekannte W. innerhalb jener Grenzen zu suchen ist. Hat man nämlich zwei, einander ausschließende Ereignisse A und B in einer großen Zahl m von Fällen beobachtet und dabei das Ereignis A µ'-mal, das Ereignis B µ,-mal gefunden, so kann man zunächst die W. für das Stattfinden des Ereignisses A gleich µ' : m , die W. für B gleich µ,: m setzen, ohne dabei den Zufälligkeiten, die der Bestimmung von µ' und µ,anhaften, Rechnung zu tragen. In der Tat kann man µ' : m und µ,: m nur als die wahrscheinlichsten Werte der unbekannten W. x und 1 x auffassen und es als wahrscheinlich bezeichnen, daß bei einer Wiederholung der Beobachtungen aus einer anderen Reihe von Fällen die nunmehr sich ergebenden wahrscheinlichsten Werte in der Nähe der früher gefundenen liegen. An Stelle dieser unbestimmten Aufstellungen gibt nun die Umkehrung des BERNOULLI'schen Theorems folgende Bestimmungen.]
[Es besteht die W. :
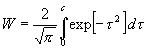 (41)
(41)
dafür, daß die unbekannte Wahrscheinlichkeit x für das Eintreten des Ereignisses A zwischen den Grenzen:
![]() und
und ![]() (41a)
(41a)
liegt; die entgegengesetzte Wahrscheinlichkeit 1 x ist dann gleichzeitig zwischen den Grenzen
![]() (41b)
(41b)
zu suchen; während für den mit der W. W zu erwartenden Unterschied u zwischen der beiderseitigen Anzahl der Fälle die Ungleichung :
[Demnach ergeben sich für m = 1000 Gewitter, die während der nämlichen Zeitperiode an zwei Orten beobachtet wurden, als wahrscheinliche Grenzen für die Werte der W., mit denen an dem einen oder anderen Orte das Stattfinden eines Gewitters zu erwarten ist:
1) an dem einen Orte 0,541 und 0,519, an dem anderen Orte 0,459 und 0,481, wenn an dem ersteren Orte 530, am letzteren 470 Gewitter beobachtet wurden.
2) an dem einen Orte 0,516 und 0,494, an dem anderen Orte 0,484 und 0,506, wenn die beiderseits beobachteten Anzahlen der Gewitter 505 resp. 495 betrugen. Entsprechend sind die wahrscheinlichen Grenzen für u im ersten und zweiten Falle 60 ± 21,29 resp. 10 ± 21,33.]
[Diesen Bestimmungen liegt die Voraussetzung unter, daß die Zahl der beobachteten Fälle hinreichend groß sei, um die Annahme zu gestatten, der beobachtete Unterschied u sei nicht rein zufällig, sondern durch die Verschiedenheit der unbekannten W. x und 1 x bedingt, und zwar wird, wie bereits angegeben, vorausgesetzt, daß die wahrscheinlichsten Werte von x , 1 x und u eben die beobachteten Werte µ' : m , µ,: m und µ¢- µ, seien.]
[Es liegt aber kein zwingender Grund vor, gerade diese Werte als die wahrscheinlichsten Werte vorauszusetzen. Denn vor Anstellung der Beobachtungen besaß jede Hypothese über die wahrscheinlichsten Werte von x und u die nämliche W., und mit Rücksicht auf die gemachten Beobachtungen kann eine dieser Hypothesen vor der anderen nur durch größere W. ausgezeichnet sein, nicht aber eine Gewißheit für sich beanspruchen. Es ist somit noch der Grad der W. zu bestimmen, den die Hypothese, die beobachteten Werte seien die wahrscheinlichsten, im Vergleiche zu anderen Hypothesen, die andere Werte als die wahrscheinlichsten einführen, besitzt. Hierzu dient das Prinzip, das ENCKE in der Abhandlung über die Methode der kleinsten Quadrate 11 ) in folgender Form gibt, wobei zu beachten, daß die Abweichungen beobachteter Werte von den wahrscheinlichsten Werten als Fehler bezeichnet werden.]
["Die W. zweier, vor den gemachten Beobachtungen gleich wahrscheinlichen und einander ausschließenden Hypothesen verhalten sich direkt wie die W. der aus ihnen hervorgehenden Fehler oder Fehlersysteme".]
[Zum Vergleiche soll die Hypothese dienen, daß die wahrscheinlichsten Werte von x und 1 x einander gleich, somit gleich ½ seien, wonach als wahrscheinlichste Differenz u = 0 zu erwarten ist. Es besitzt alsdann die tatsächlich beobachtete Differenz u die W.:
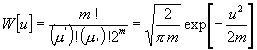 .
(42)
.
(42)
Auf Grund der bisherigen Hypothese, daß die wahrscheinlichen Werte von x und 1 - x resp. µ' : m = p und µ,: m = q seien, ergibt sich dagegen für das beobachtete u der Maximalwert der W., nämlich:
![]() .
(43)
.
(43)
Es verhält sich somit die W., daß das beobachtete u rein zufällig sei, d. h. bei Gleichheit von x und 1 x sich ergeben habe, zu der W., daß das beobachtete u den wahrscheinlichsten Differenzwert der beiderseitigen Anzahlen µ' und µ,darstelle, wie
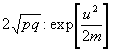 oder wie
oder wie 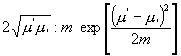 ; (44)
; (44)
und will man wetten, so müssen die Einsätze
das angegebene Verhältnis aufweisen.]
Setzt man nun einerseits voraus, der beobachtete Unterschied u = ± (µ' - µ,) sei rein zufällig, so besteht nach dem G. G. die W. Ww , daß dieser Wert nicht erreicht, und die W. 1 - Ww , daß er erreicht oder überschritten wird. Setzt man andererseits voraus, jener Unterschied sei nicht zufällig, sondern seiner Natur nach gleich u oder größer als u , so ist die W., daß er erreicht oder überschritten wird gleich 1 zu setzen. Es überbietet somit die W., der beobachtete Wert u sei seiner Natur nach gleich oder größer als u , die W., er sei bloß zufällig, um Ww , so daß die überwiegende Wahrscheinlichkeit Wwfür das Fehlen reiner Zufälligkeit der Wahrscheinlichkeit 1 - Ww für das Bestehen reiner Zufälligkeit gegenübersteht, und in diesem Verhältnisse wird alsdann gegen und für reine Zufälligkeit gewettet.]