![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
§ 97. Wenn schon oben Merkmale zur Unterscheidung der wesentlichen von der unwesentlichen Asymmetrie gegeben sind, ist doch zu gestehen, daß sie keinen absoluten Charakter haben. Auch kann man in der Tat nie absolut versichern, daß eine wesentliche Asymmetrie vorliegt, sondern nur, daß eine überwiegende Wahrscheinlichkeit für dieselbe besteht, eine um so mehr überwiegende, je mehr die oben angegebenen Unterscheidungsmerkmale von der zufälligen bestehen und zusammentreffen.
Um doch ein etwas bestimmteres Wahrscheinlichkeitsurteil zu fällen, ist es nützlich, zu wissen, welchen Unterschied man nach W. und im Durchschnitte schon bei wesentlicher Symmetrie nach bloßer Zufälligkeit zu finden erwarten kann.
Unter wahrscheinlicher Differenz verstehe ich diejenige, die in einer großen, streng genommen unendlichen Zahl von Fällen eben so oft unterschritten (nicht erreicht), als überschritten wird; unter mittlerer oder durchschnittlicher die, die man erhält, wenn man die bei oft wiederholten Versuchen mit gegebenem m erhaltenen Werte von u ohne Rücksicht auf das Vorzeichen addiert und mit der Zahl n der vorgenommenen Wiederholungen dividiert. In der Tat, hat man den einen oder anderen beider Werte für den Fall wesentlicher Symmetrie allgemein bestimmt, so wird man jeden, bei einer gegebenen Mittelbestimmung erhaltenen Wert von u damit vergleichen können. Überwiegt er jene Werte in starkem Verhältnisse, so wird man es sehr unwahrscheinlich zu finden haben, daß er bei Symmetrie erreicht werden konnte, weil die Unwahrscheinlichkeit davon mit der Größe dieses Übersteigens wächst, hiergegen eine wesentliche Asymmetrie vom Vorzeichen des u sehr wahrscheinlich halten dürfen. Bleibt er erheblich unter diesen Werten, so hat man mit großer W. auf Symmetrie oder geringe Asymmetrie von zweifelhaftem Vorzeichen zu schließen. Ja, man kann noch genauere Schlüsse ziehen. Die Theorie lehrt, und die Erfahrung bestätigt es, daß die Wahrscheinlichkeitsverhältnisse, welche nach G. G. für die Beobachtungsfehler im Sinne des bekannten, tabellarisch darstellbaren Integrals bestehen, sich bei wesentlicher Symmetrie auf die u in der Art übertragen lassen, daß das Übersteigen des mittleren oder wahrscheinlichen u bis zu gegebenen Grenzen gleicher W. unterliegt wie das Übersteigen des einfach mittleren oder wahrscheinlichen Beobachtungsfehlers.
Dies wird ausführlicher und genauer in den beiden folgenden Kapiteln theoretisch erwiesen, empirisch bewährt und die Anwendung davon gezeigt werden. Hier beschränke ich mich, vorgreiflich folgende Hauptbestimmungen daraus zu entlehnen, welche geeignet sind, den allgemeinsten Anhalt zu geben.
§. 98. Man hat dabei zwei Fälle zu unterscheiden, den eigentlich nur idealen Fall, daß die Werte D vom wahren A gerechnet werden, wie es aus einer unendlichen Zahl von Einzelwerten, also im absoluten Normalfalle zu erlangen sein würde, und den Fall der Wirklichkeit, wo sie von dem in gewisser Weise unrichtigen A gerechnet werden, wie es aus einer endlichen Zahl von Werten zu erlangen ist. Erstenfalls ist gleichgültig, welchem Gesetze der Verteilung die einzelnen Werte nach Maß und Zahl gehorchen, nicht die Größe, nur die Zahl derselben bei gleicher W. der + und - kommt in Betracht, und man kann den bekannten Sack mit einer gleichen Anzahl weißer und schwarzer Kugeln statt + und - als Anhalt zur Berechnung nehmen. Letztenfalls muß für die theoretische Berechnung des mittleren und wahrscheinlichen u ein bestimmtes Gesetz der Verteilung zu Grunde gelegt werden, weil sich hiernach die durchschnittlich und wahrscheinlich zu erwartende Abweichung des falschen vom wahren A richtet, und diese wieder auf die Größe des durchschnittlichen und wahrscheinlichen u von Einfluß ist. Wir legen demgemäß zweitenfalls für die Verteilung das G. G. zufälliger Abweichungen vom Beobachtungsmittel unter, welches durch das bekannte Integral dargestellt wird, da diese Verteilung als normal für den idealen Fall eines wesentlich symmetrischen K.-G. gelten kann.
Sei nun U das mittlere, V das wahrscheinliche u in dem soeben (§ 97) angegebenen Sinne unter Voraussetzung des ersten Falles, U und V unter Voraussetzung des zweiten Falles 1), so hat man, bis zu sehr kleinem m merklich zutreffend folgende Normalbestimmungen:
![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
log 0,48097 = 0,68212 - 1 , log 0,40659 = 0,60916 - 1 .
l ) V und V haben sonach hier eine andere
Bedeutung als die in § 10 festgesetzte.
§ 99. Hierzu folgende Bemerkungen. Sämtliche vier Formeln sind prinzipiell nur als approximative für größere m hergeleitet, und bei dieser Herleitung die mit ± behafteten Korrektionen 0,5 und 1,5 der Werte U und U (die füglich gegen größeres m verschwindet) nicht mit gefunden. Aber es findet sich empirisch, daß durch Anbringung derselben die betreffenden Formeln bis zu viel kleineren m – ja fast bis zu den kleinsten – herab merklich zutreffend werden als ohne sie.
Ein Erfolg der Korrektion ± 0,5 für U ist, daß der Wert desselben für jedes ungerade und das nächst größere gerade m gleich groß ist, und ein Erfolg der Korrektion ± 1,5 für U , daß der Wert für jedes ungerade und das um 3 Einheiten größere gerade m gleich groß ist. Durch Rückgang auf ganz genaue Formeln für U, welche aber bei größerem m zu umständlich in der Anwendung werden, läßt sich beweisen, daß der erste Erfolg normalerweise von dem kleinsten bis zu dem größten m streng und allgemein gültig ist; was den zweiten anlangt, so kann ich dasselbe nicht mit gleicher Sicherheit, sondern nur nach den in Kap. XVI folgenden empirischen Ergebnissen behaupten, welche diesen Erfolg so nahe, als man es nach der Unsicherheit solcher Ergebnisse erwarten kann, zeigen; auch ist die theoretische Herleitung der gegebenen Formeln für U und V nicht ganz so sicher als für U und V , und da doch gerade von jenen allein für unsere jetzige Untersuchung eine praktische Anwendung zu machen ist, indes die für U und V in anderen Untersuchungen größere Wichtigkeit gewinnen, so ist diesbezüglich auf die nach einer sehr eigentümlichen, sehr mühsamen Methode von mir erlangten, empirischen Bewährungsresultate für U und V in § 115 zu verweisen.
Es wird nützlich sein zu bemerken, daß die vorigen Formeln auch für den Fall Anwendung finden können, wenn man statt des m einer einzelnen Serie das summatorische åm mehrerer, bezüglich verschiedener Mittel erhaltener Serien, sei es mit gleichem oder verschiedenem m vor sich hat, indem sich dann dies åm für m in vorigen Formeln substituiert; nur muß dabei die Bedingung erfüllt sein, daß die Zufälligkeiten, welche in den einzelnen Serien auf die Größe des u Einfluß haben, als ebenso unabhängig von einander angesehen werden können, und mithin bei Zusammenrechnung der verschiedenen m entsprechend zur Kompensation tendieren, als wenn man das m derselben Serie vergrößert.
§ 100. Noch möchten einige theoretische Bedenken zu heben sein, die sich bei Betrachtung der vorigen Formeln leicht aufdrängen könnten.
Nach der bei vorigen Formeln vorausgesetzten gleichen Wahrscheinlichkeit der D ' und D, hatte man im Sacke mit unendlich vielen weißen und schwarzen Kugeln, welche uns die D ' und D,vertreten können eine gleiche Anzahl beider anzunehmen; und wenn die ganze unendliche Anzahl gezogen würde, das m des Zuges also unendlich wäre, so sollte hiernach der Unterschied u Null sein und zwar bei jeder Wiederholung eines solchen Zuges Null sein, also auch der mittlere und wahrscheinliche Unterschied Null sein, wogegen die Formeln einen, mit m ins Unbestimmte wachsenden und bei m = ¥ unendlichen Wert von U , V , U , V finden lassen.
Von anderer Seite jedoch leuchtet ein, daß mit wachsendem m auch der Spielraum eines möglichen zufälligen Unterschiedes zwischen µ' und µ,sich vergrößert, und insofern allerdings ein Wachstum des mittleren und wahrscheinlichen Unterschiedes mit m erwartet werden kann, wovon keine Grenze abzusehen ist, hiernach bei unendlichem m in der Tat ein unendlicher Unterschied erwartet werden kann.
Diese scheinbare Antinomie hebt sich
dadurch daß, wenn schon der mittlere und wahrscheinliche Unterschied
bei unendlichem m den Formeln gemäß an sich selbst unendlich
groß wird, er doch als mit ![]() proportional, als Größe zweiter Ordnung, gegen m sowohl
als µ' und µ,,
die selbst mit m gleicher Ordnung sind, verschwindet, so daß
man aus diesem mathematischen Gesichtspunkte das größtmögliche
µ' , was sich ziehen läßt, immer noch gleich µ,,
oder µ' : µ,der
Einheit gleich setzen kann, wie es als Bedingung der Symmetrie festzuhalten
ist, wenn schon µ¢ von µ,sich
um eine gegen beide verschwindende Größe unterscheidet.
proportional, als Größe zweiter Ordnung, gegen m sowohl
als µ' und µ,,
die selbst mit m gleicher Ordnung sind, verschwindet, so daß
man aus diesem mathematischen Gesichtspunkte das größtmögliche
µ' , was sich ziehen läßt, immer noch gleich µ,,
oder µ' : µ,der
Einheit gleich setzen kann, wie es als Bedingung der Symmetrie festzuhalten
ist, wenn schon µ¢ von µ,sich
um eine gegen beide verschwindende Größe unterscheidet.
Auch kann man vielleicht die Sache so fassen: Da eine Unendlichkeit mit einer Unendlichkeit multipliziert gedacht werden kann, was wieder eine Unendlichkeit gibt, so folgt daraus, daß man einfach eine unendliche Zahl Kugeln zieht, nicht, daß man die ganze Zahl zieht, und es könnte immerhin in der absoluten Unendlichkeit die Zahl der weißen und schwarzen Kugeln gleich sein, ohne daß bei m = ¥ diese Gleichheit einträte, sofern das ¥ nicht die absolute Unendlichkeit bedeutete.
Jedenfalls kann man der Erfahrung nicht anders als durch obige Gestalt der Formeln entsprechen, und rechtfertigt sich hierdurch dieselbe gegen jedes Bedenken der Theorie, was aus vorigem Gesichtspunkte übrig bleiben könnte.
Zweitens kann man aufstellen, daß, da mit wachsendem m der Unterschied zwischen dem wahren und falschen A sich mehr und mehr verkleinert und bei unendlichem m verschwindend klein wird doch nach obigen Formeln das vom falschen A gerechnete U zu dem vom wahren A gerechneten U ein bei größerem m merklich konstantes Verhältnis hat, dessen genauer Grenzwert für unendliches m statt 1 vielmehr
![]() (5)
(5)
ist.
Dies aber hat folgenden Grund: Die Zahl von Abweichungen, welche zwischen dem wahren und dem falschen Mittel liegen, und wovon der Unterschied zwischen U und U abhängt, nimmt freilich mit der Annäherung des falschen an das wahre Mittel ab, aber mit der Größe des m zu; und insofern die Annäherung beider Mittel durch die Größe des m bedingt wird, kompensiert sich dies so, daß jenes konstante Verhältnis bei wachsendem m herauskommt; und selbst bei unendlicher Annäherung beider Mittel kann vermöge Unendlichkeit des m noch eine unendliche Menge unendlich kleiner Abweichungen zwischen beiden mathematisch liegend gedacht werden. Auch in dieser Hinsicht ist übrigens die Erfahrung entscheidend. Nach den in § 115 angeführten, mit einander vergleichbaren Werten von U und U findet man für m = 10; 50; 100 der Reihe noch den Wert U : U gleich 0,554; 0,558; 0,608, was von dem theoretischen Verhältnisse und von der Konstanz nur in den Grenzen der zu erwartenden Unsicherheit abweicht, die natürlich für das Verhältnis zweier Werte erheblich größer als für die Einzelwerte ist.
Drittens kann der folgende Umstand
auffallen. Je nachdem man Abweichungen vom wahren oder falschen Mittel
rechnet, fällt die Summe derselben verschieden aus, und zwar durchschnittlich
um so kleiner bei Rechnung vom falschen Mittel gegen die Rechnung vom wahren
Mittel, je kleiner m und je falscher mithin das Mittel ist. Aber
der Unterschied ist schon bei mäßigem m fast verschwindend,
indem, wie ich in einer besonderen Abhandlung2)
theoretisch und empirisch gezeigt, die falsche zur wahren Summe sich durchschnittlich
wie ![]() zu
zu ![]() verhält,
welches Verhältnis mit wachsendem m sich der Einheit rasch
nähert. Hiergegen erscheint auffällig, daß der mittlere
Unterschied zwischen der Zahl der positiven und negativen Abweichungen
so beträchtlich verschieden ist, als sich nach obigem Grenzverhältnis
U : U =
0,6028 ergibt.
verhält,
welches Verhältnis mit wachsendem m sich der Einheit rasch
nähert. Hiergegen erscheint auffällig, daß der mittlere
Unterschied zwischen der Zahl der positiven und negativen Abweichungen
so beträchtlich verschieden ist, als sich nach obigem Grenzverhältnis
U : U =
0,6028 ergibt.
2 ) ["Über die Korrektionen bezüglich der Genauigkeitsbestimmung
der Beobachtungen" etc. in den Berichten der Kgl. Sächs. Gesellschaft
der Wissenschaften. 1861.]
Dies läßt sich wie folgt verständlich machen. Wenn die Abweichungen, die man in Wirklichkeit erhält, vom wahren Mittel gerechnet werden könnten, würde bei endlichem m nicht nur die Zahl, sondern auch die Summe derselben nach beiden Seiten nach Zufall ungleich sein. Nun geschieht die Bestimmung des falschen Mittels so, daß man die Summen der D nach beiden Seiten künstlich gleich macht, da dies ja die Bedingung des arithmetischen Mittels ist, und man hätte hiernach zu erwarten, daß mit dem Summenunterschiede auch der Zahlenunterschied bei Rechnung von falschem Mittel ganz verschwände, wenn beide Unterschiede proportional gingen. Dies ist nun nicht der Fall; aber jedenfalls sieht man ein, daß das Verschwinden des Summenunterschiedes beim Übergange vom wahren zum falschen Mittel recht wohl mit einer so bedeutenden Reduktion des Zahlenunterschiedes zusammenhängen kann, wie sie sich im Verhältnisse U : U herausstellt.
Was die wesentliche Asymmetrie anlangt, so nimmt sie an dieser Reduktion nur geringen Anteil. Wie oben (Kap. XIII) bemerkt, kann sich zwar weder wesentliche, noch unwesentliche Asymmetrie bei gar zu kleinem m recht entwickeln; indem aber die Abweichung des falschen vom wahren Mittel durchschnittlich ebenso oft im Sinne als wider den Sinn der wesentlichen Asymmetrie geschieht, findet bei großem m eine Kompensation des Einflusses hiervon für die wesentliche Asymmetrie statt.
§101. [Zusatz. Um schließlich noch die Modifikationen, welche die obigen Formeln für den Fall der wesentlichen Asymmetrie erleiden, anzugeben und zugleich die Triftigkeit des im vorigen Kapitel gegebenen Schemas der Mischung von wesentlicher und unwesentlicher Asymmetrie zu erweisen, ist zu beachten, daß bei wesentlich asymmetrischen K.-G. nicht vom arithmetischen Mittel, sondern vom dichtesten Werte prinzipiell auszugehen ist. Bezüglich des letzteren Wertes sind dann die Wahrscheinlichkeiten positiver und negativer Abweichungen nicht gleich, sondern, in Übereinstimmung mit der theoretischen Bestimmung des dichtesten Wertes, im Verhältnisse der beiderseitigen einfachen mittleren Abweichungen e' und e, anzunehmen. Denn die Proportion e' : e,= m' : m,definiert den dichtesten Wert, so daß die Gesamtzahl der Exemplare sich im Verhältnisse e' : e, auf beide Seiten des dichtesten Wertes verteilt, und mithin eben dies Verhältnis die Wahrscheinlichkeiten p und q = 1- p für positive und negative Abweichungen bestimmt. Es sei demgemäß für einen K.-G. mit gegebenem e' und e, bez. des dichtesten Wertes 3):
![]() ;
; ![]() (6)
(6)
Dann ist zunächst die wahrscheinlichste Differenz zwischen positiven und negativen Abweichungen für ein beliebiges m gleich:
![]()
![]() (8)
(8)
(p - q)m ± 0,6745 ×![]() ,
(10)
,
(10)
d. h. es ist 1 gegen 1 zu wetten, daß ein beobachtetes
u größer als (p - q)m - 0,6745![]() und kleiner als (p - q)m + 0,6745
und kleiner als (p - q)m + 0,6745![]() sei.]
sei.]
3) [Eine eingehendere Diskussion lehrt, daß bei schwacher
Asymmetrie die eine arithmetische Behandlung des K.-G. gestattet, p
und q nur um Größen von der Ordnung 1:![]() ,
wo m die Gesamtzahl der Exemplare des K.-G. ist, von ½ verschieden
sind.]
,
wo m die Gesamtzahl der Exemplare des K.-G. ist, von ½ verschieden
sind.]
[Diese Bestimmung der wahrscheinlichen
Grenzen läßt zugleich die Mischungsverhältnisse der wesentlichen
und unwesentlichen Asymmetrie erkennen, wenn im Einklange mit den Aufstellungen
des vorhergehenden Kapitels unter wesentlicher Asymmetrie der wahrscheinlichste,
von Null verschiedene Differenzwert u , unter unwesentlicher Asymmetrie
die wahrscheinliche Schwankung um diesen wahrscheinlichsten Wert verstanden
wird. Sie zeigt, daß man in Formel (3) des angegebenen Kapitels x1
= (p - q)m; y1 = 0,6745![]() setzen kann, und daß man sodann in Formel (2), wo p = q
= ½ anzunehmen ist, y1 =
0,6745
setzen kann, und daß man sodann in Formel (2), wo p = q
= ½ anzunehmen ist, y1 =
0,6745 ![]() zu setzen hat.]
zu setzen hat.]
[Man gelangt zu den angegebenen Bestimmungen des wahrscheinlichsten u , sowie der mittleren und wahrscheinlichen Schwankung um diesen Wert, wenn man die Wahrscheinlichkeit, daß unter m Abweichungen m' positive und m,, negative sich finden, daß mithin u = m' - m,, gleich:
![]() (11)
(11)
setzt und hieraus unter Voraussetzung eines großen Wertes von m den Näherungswert:
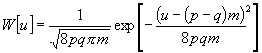 (12)
(12)
ableitet]