![]() ; (1)
; (1)
§ 87. [Da der dichteste Wert als Ausgangswert des für K.-G. in Anspruch zu nehmenden Verteilungsgesetzes eine fundamentale Stellung in der Kollektivmaßlehre einnimmt, so ist eine Erörterung seiner mathematischen Bedeutung und seiner, auf letztere zu gründenden rechnerischen Bestimmung notwendig. Hierbei ist es wesentlich, den als Di bezeichneten empirisch dichtesten Wert, den die Tafel hergibt, von dem als Dpbezeichneten theoretisch wahrscheinlichsten Wert, den das Verteilungsgesetz verlangt, zu scheiden und jeden gesondert zu behandeln.]
[Die Existenz von Di gründet sich darauf, daß die z der Tafel, die für einen K.-G. die Anzahl der Exemplare von der Größe a angeben, nicht durchweg konstant sind, sondern steigen und fallen. So lange nun bei roher Bestimmung die z direkt als den beigeschriebenen a zugehörig aufgefaßt und demgemäß die zwischen die gemessenen a der Tafel fallenden a-Werte als überhaupt nicht vorkommend angesehen werden, kann nur das mit dem größten z behaftete a selbst als dichtester Wert beansprucht werden; und es gibt alsdann kein Mittel, für den Fall, daß mehrere aufeinander folgende a das nämliche Maximal-z besitzen, den Zweifel, welches a nun in Wirklichkeit den dichtesten Wert darstelle, zu heben 1). Wird aber berücksichtigt, daß die Intervalle zwischen den gemessenen a nur der relativ geringen Anzahl der gemessenen Exemplare und der Ungenauigkeit der Messung ihr Dasein verdanken, während die unbegrenzte Gesamtheit der Exemplare des K.-G. sich ohne Unterbrechung auf alle, zwischen den Extremen liegende a verteilt, so hat man in den gegebenen Tafelwerten nur die Unterlage zu suchen, auf der ein funktioneller Zusammenhang zwischen den z und den a sich aufbaut. Ist derselbe hergestellt, so ergibt sich der dichteste Wert in einfacher Weise als Maximum der konstruierten Funktion.]
1) [Das Vorkommen von zwei einander gleichen, durch Zwischenwerte getrennten Maximal-z ist nicht zu berücksichtigen, da dies das Auftreten von zwei verschiedenen dichtesten Werten bedingen und so eine Mi-schung disparater K.-G., auf welche die Verteilungsgesetze keine direkte Anwendung finden, anzeigen würde.]
[Bei der Herstellung dieses funktionellen Zusammenhanges ist nun darauf zu achten, daß was schon durch die Ungenauigkeit der Messung und durch die daraus folgende Existenz der primären Intervalle bedingt ist die z der Tafel nicht als Einzelwerte der gesuchten Funktion, sondern als Summenwerte; die auf die zugehörigen Intervalle zu beziehen, mithin als Integralwerte, genommen für die Grenzen der Intervalle, zu gelten haben. Im übrigen sind die Prinzipien der Interpolationsrechnung in Anwendung zu bringen, was darauf hinauskommt, die Anzahl der Exemplare von der Größe a , die allgemein mit z bezeichnet werde, innerhalb eines bestimmten Bereiches als eine ganze rationale Funktion von a vorauszuset-zen und dann mittelst der gegebenen z der Tafel ihre Koeffizienten so zu bestimmen, daß die Summen der z , d. i, ihre Integrale zwischen den Grenzen der in Betracht gezogenen Intervalle, mit den gegebenen z der Tafel für eben dieselben Intervalle übereinstimmen; dabei ist die Anzahl der zu berücksichtigenden, aufeinanderfolgenden Intervalle von dem Grade der vorausgesetzten Funktion oder der Anzahl der zu bestimmenden Koeffizienten abhängig, und es wächst mit dem Steigen jener Anzahl zugleich der Grad der erreichten Genauigkeit.]
[Wird also vorausgesetzt, daß für den Bereich eines Wertes a , der in dem Intervall mit der Mitte a0 und mit einem z gleich z0 liege, z entweder konstant sei oder durch eine lineare Funktion von a oder durch eine solche vom zweiten Grade dargestellt werde, so ist im ersten Falle nur das z0des Intervalles selbst, im zweiten Falle das z eines der beiden benachbarten Intervalle, im dritten Falle das z der beiden Nachbarintervalle zu benutzen, um die Konstanten zu bestimmen. Man findet so, wenn das z des nach dem oberen Extrem zu gelegenen Intervalles mit z1 , das in entgegengesetzter Richtung liegende mit z-1bezeichnet und die in Erstreckung der ganzen Tafel sich behauptende Intervallgröße nach früherer Festsetzung i genannt wird, im ersten Falle:
![]() ; (1)
; (1)
im zweiten Falle:
![]() oder =
oder = ![]() ; (2)
; (2)
im dritten Falle:
![]() ; (3)
; (3)
Formeln, deren Gültigkeitsbereich in jedem Falle über das Intervall mit den Grenzen a0 - ½i und a0 + ½i sich erstreckt.]
[Will man nun auf Grund der so konstruierten funktionellen Abhängigkeit das dichteste a des Intervalles bestimmen, so erweist sich bloß die Formel (3) hierzu brauchbar; denn (1) liefert durchweg konstante, (2) ständig wachsende oder ständig abnehmende Werte. Aus (3) aber ergibt sich der Maximalwert oder dichteste Wert:
![]() , (4)
, (4)
sofern nur 2z0 - z1 - z-1 > 0 . Ist letzterer Wert kleiner als Null, so stellt a ein Minimum dar, ist aber 2z0 - z1 - z-1 = 0 , so wird (3) linear und zur Bestimmung eines Maximums unbrauchbar. Soll überdies, wie erforderlich, das Maximum innerhalb des untersuchten Intervalles liegen, so muß sowohl z1als auch z-1 , jedes für sich, kleiner als z0 sein.]
[Statt auf die Mitte a0kann sich die Bestimmung des dichtesten Wertes auch auf die Grenzen des Intervalles: g1= a0 - ½i und g2 = a0 + ½i beziehen. Man findet, wenn a - g1 = x gesetzt wird:
![]() ; (5)
; (5)
![]()
woraus die einfache Proportion:
[Die Bestimmung von Dierledigt sich mithin mittelst obiger Formeln, indem zunächst das Intervall mit dem Maximal-z , d. i. der roh bestimmte dichteste Wert, aufgesucht, und dann die Lage von Diinnerhalb dieses Intervalles durch den Ansatz der Proportion (6) oder aus den Gleichungen (5) oder (4) berechnet wird. Existiert nur ein Maximal-z , so ist die erreichte Genauigkeit hinreichend, und die Beiziehung schärferer Interpolationsformeln unter Berücksichtigung der z von vier oder mehr benachbarten Intervallen im allgemeinen nicht nötig. Ja man gewinnt selbst auch dann noch eine brauchbare Bestimmung, wenn zwei benachbarte Maximal-z die rohe Bestimmung des dichtesten Wertes im Ungewissen lassen. Es wird nämlich, wenn z0 = z-1 , x = 0, und wenn z0 = z1, x = i , so daß stets die gemeinsame Grenze der beiden, mit dem Maximal-z behafteten Intervalle als Di in Anspruch zu nehmen ist.]
§ 88. [Auf diesem Wege wurden die Werte Di der verschiedenen Reduktionsstufen und Reduktionslagen des VIII. Kap. berechnet. Nicht anders wird es in den späteren Kapiteln gehalten werden. Es kann indessen erwünscht sein, für den Fall, daß zwei benachbarte Maximal-z auftreten, eine schärfere Formel zur Verfügung zu haben. Ja es wäre eine solche unumgänglich, wenn was allerdings kaum zu erwarten ist und eintretenden Falles durch Änderung der Reduktionslage vermieden werden kann drei succedierende Maximal-z das Versagen der obigen Formeln bedingen würden. Dann ist noch ein weiteres Intervall zu den bisher berücksichtigten hinzuzunehmen, um z als eine Funktion dritten Grades bestimmen zu können. Es sei dies das auf das Intervall mit z = z1 folgende Intervall mit z = z2 . Setzt man nun wie oben a = g1 + x oder = g2 - (i - x), wo g1 und g2 die untere und obere Grenze des Intervalles mit der Mitte a0und z = z0sind, so ergibt sich:
![]() . (8)
. (8)
Man findet ferner:
![]() , wenn z2 = z1
= z0 ;
, wenn z2 = z1
= z0 ;
![]() , wenn z-1 = z1
= z0 (9)
, wenn z-1 = z1
= z0 (9)
wonach die Lage von Di wechselt, je nachdem man das auf die drei Maximal-z folgende oder das vorhergehende Intervall berücksichtigt. Dieser Unsicherheit kann nur durch Beiziehen der beiden Nachbarintervalle begegnet werden.]
[Geschieht dies, indem man z0 = z1 = z-1annimmt und außer dem folgenden Intervall mit z = z2 noch das vorangehende Intervall mit z = z-2 berücksichtigt, so erhält man zur Bestimmung des Maximums, für x = a - g1 , die Gleichung:
a + 2bx + 3gx² + 4dx³ = 0 ;
12i²a= - z0 + z-2 ; 8i³b = z-2 z2; 6i4g = z0 z-2; (10)
24i5d= - 2z0 + z2 + z-2 ;
mit der Bedingung:
§ 89. [Während so die Existenz von Di unabhängig von dem Bestehen eines Verteilungsgesetzes ist, und seine Bestimmung in sukzessiver Annäherung durch Interpolation erreicht werden kann, wird die Existenz von Dp gerade durch das vorausgesetzte Verteilungsgesetz, unseren Falles durch das zweiseitige G. G., gefordert, und seine Berechnung aus den gegebenen Tafelwerten ist auf Grund seiner mathematisch formulierten Eigenschaften vorzunehmen. Es würde zwar, wenn die unvermeidlichen, unausgeglichenen Zufälligkeiten ein genaues Zutreffen des Verteilungsgesetzes nicht hindern würden, der dichteste Wert von vorn herein die Eigenschaften von Dpbesitzen, mithin Di= Dp sein; und es wäre alsdann kein Anlaß vorhanden, neben Dinoch Dpzu berechnen, wenn nicht auch in diesem Falle die scharf formulierten Eigenschaften von Dpeine größere Sicherheit als die Annäherungen des Interpolalionsverfahrens böten. Insofern aber der Gang der Tafelwerte niemals völlig den Forderungen des Gesetzes entspricht, weichen Di und Dp auseinander; und es muß unabhängig von Di auch Dp bestimmt werden, um sowohl in dem Unterschiede ihrer Lage einen Maßstab für das Zutreffen des Verteilungsgesetzes zu gewinnen, als auch in Dpeinen geeigneteren Augangswert wie in Di zur Anwendung jenes Gesetzes zu erhalten.]
[Es wird nun Dp, in solidarischem Zusammenhange mit dem zweiseitigen G. G., durch die Eigenschaft definiert, daß die Anzahlen der unteren und oberen Abweichungen bezüglich desselben sich verhalten wie die Mittelwerte der unteren und oberen Abweichungen, oder daß:
[Zu diesem Zwecke setze man eine Verteilungstafel mit äquidistanten a voraus, deren z das eine Mal durchweg konstant, das andere Mal durchweg das nämliche Vielfache der zugehörigen a darstellen.]
[Im ersteren Falle sind die z gleichmäßig auf die ganze Tafel zu verteilen; es ist mithin, zwischen den Grenzen a = b und a = c :
z = a ,
wo a eine Konstante bedeutet; und für ein beliebiges a findet man:
m, = a(a - b) ; m' = a (c - a) ,
[Im zweiten Falle ergibt sich durch Interpolation die stetige Verteilung:
![]() ;
;![]() ;
;
![]() ;
; ![]() ;
;
so daß als Lösungen der Gleichung:
[Infolge dieses Vorkommens kann es wünschenswert erscheinen, ein Kriterium für das Vorhandensein von Dp zu besitzen. Ein solches bietet sich in einfacher Weise durch folgende Erwägung. Ist für den Beginn der Tafel nachweisbar e,:m, > e' : m' , für das Ende e,:m,< e' : m,so muß für einen mittleren Wert e,: m, = e' : m' sein, da die Quotienten e,:m, und e' :m' infolge der stetigen Verteilung der z auf die einzelnen Intervalle sich mit der Lage des Wertes, auf den sie sich beziehen, stetig ändern. Nun ist aber, wenn za das z von E,, zw dasjenige von E' darstellt und die untere Grenze des Intervalles von E, mit b , die obere Grenze des Intervalles von E' mit c bezeichnet wird, für den Anfang der Tafel:
![]() ;
; ![]() ;
;
für das Ende der Tafel:
![]() ;
; ![]() .
.
Es existiert daher jedenfalls ein Wert Dpinnerhalb der Tafel, wenn:
![]() ;
; ![]() ist.]
(12)
ist.]
(12)
§ 90. [Zur Berechnung von Dpkann zunächst nur die Proportion (11) dienen, da sie diesen Wert definiert. Es lassen sich jedoch auf Grund jener Proportion folgende Eigenschaften des Wertes Dpnachweisen, die in gleicher Weise zu einer Berechnung benutzt werden können:
![]() , (15)
, (15)
wo u = m' - m,. Durch Addition und Subtraktion von (14) und (15) gewinnt man ferner:
![]()
![]() (16)
(16)
Der Beweis von (13) wird erbracht, indem durch Substitution der Werte
![]() ;
; ![]() (17)
(17)
in die aus der Proportion (11) sich ergebende Gleichung e' m,= e,m¢ mittelst einfacher Rechnung die Gleichung:
![]() (18)
(18)
hergeleitet und in derselben
![]() ;
; ![]()
gesetzt wird. In der Tat folgt aus der so resultierenden Gleichung:
![]() (19)
(19)
durch Division mit m die Formel (13). Ist aber diese Formel gewonnen, so folgt aus ihr, wenn åa,:m, und åa¢ : m' aus (17) durch Dp und e,resp. e' ausgedrückt werden, unmittelbar die Gleichung (14).]
§ 91. [Zur rechnerischen Bestimmung von Dp bietet nun die Gleichung (13) den bequemsten Ansatz. Hierzu ist jedoch eine Kenntnis des Intervalles, in das Dp fällt, erforderlich, da die Eigenschaften des gesuchten Wertes auf die Abweichungszahlen und Abweichungssummen sich gründen und nicht eine absolute Bestimmung, wie sie für A möglich ist, gestatten. Es muß somit, wo eine solche Kenntnis, die z. B. durch vorgängige Berechnung von Di erworben werden kann, fehlt, versuchsweise der Ansatz für irgend ein Intervall gemacht und, wenn nicht zufällig das richtige Intervall getroffen wurde, für ein anderes Intervall wiederholt werden, wobei indessen das Ergebnis der zuerst geführten, fehlschlagenden Rechnung die Wahl des Intervalles bei der Wiederholung des Versuches zu beeinflussen hat. Bietet die Tafel keine großen Abnormitäten, so wird es sich bei diesen Versuchen nur um die Wahl zwischen benachbarten Intervallen handeln.]
[Hat man demgemäß ein bestimmtes Intervall, dessen Mitte a0 , dessen untere Grenze g1 und dessen z gleich z0 sei, als Eingriffsintervall gewählt und für dasselbe v, n, V,N berechnet, so ist bei roher Bestimmung in Übereinstimmung mit (13):
![]() ; (20a)
; (20a)
oder:
![]() ; (20b)
; (20b)
je nachdem Dp kleiner oder größer als a0 . Es ist somit die erstere Formel zutreffend, wenn a0 - Dp < ½i , die letztere, wenn Dp - a0 < ½i sich ergibt.
![]() (21)
(21)
![]() ;
; ![]() ;
;
so erhält man folgende Gleichung für x = Dp - g1 ;
![]() ;
;
2 ) [Wollte
man die einfacher scheinende, jedoch ungenauere Formel (6) des Kap. IX,
nämlich Y = a0z0x
: I, benutzen, so würde an Stelle von (22) eine Gleichung dritten
Grades für x resultieren; es hätte somit der Verlust an
Genauigkeit überdies eine Einbuße an rechnerischer Bequemlichkeit
zur Folge.]
[Da jedoch diese Bestimmungsweise keineswegs bequem ist, soll Dp zu irgend einem in dem nämlichen Intervall liegenden Hauptwerte H in Beziehung gesetzt werden, um auf Grund der besonderen Eigenschaften des jeweils gewählten H einfachere Gleichungen zu gewinnen.]
[Zu diesem Zwecke mögen die Anzahlen und die Summen der unterhalb und oberhalb H gelegenen a durch m", m" , å a", å a" bezeichnet, ferner Dp - H = x' und die zwischen Dpund H liegenden a ihrer Anzahl nach gleich y' , ihrer Summe nach gleich Y' gesetzt werden, so daß:
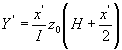 ;
; ![]() .
.
Man gewinnt dann aus dem Ansatze:
![]() (23)
(23)
für x' = Dp - H die Gleichung:
a¢x¢² - b¢ x¢ + g¢ = 0 ;
![]() ;
;
![]() ; (24)
; (24)
![]() ;
;
die für H = g1in (22) übergeht. Aus derselben muß sich ein x' ergeben, das entweder positiv und kleiner als g2- H (wo g2die obere Grenze des Eingriffsintervalles ist), oder negativ und seinem absoluten Werte nach kleiner als H - g1ist.]
[Diese Gleichung führt nun, wenn entweder das arithmetische Mittel A oder der Zentralwert C oder der Scheidewert R in das Intervall von Dpfällt und als H gewählt wird, zu folgenden Bestimmungen :
![]() ;
(25)
;
(25)
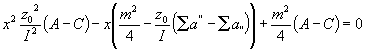 ; (26)
; (26)wo åa" und åa" auf C sich beziehen.
![]()
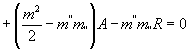 ; (27)
; (27)
[Der Anwendungsbereich dieser Bestimmungsweisen wird noch erweitert, wenn man für den Fall, daß Dpund der Hauptwert, auf den die Rechnung Bezug nimmt, in benachbarte Intervalle fallen, eine Verschiebung des Eingriffsintervalles vornimmt oder, mit anderen Worten, das Eingriffsintervall aus aneinanderstoßenden Teilen zweier Nachbarintervalle zusammensetzt. Das z0dieses zusammengesetzten Intervalles setzt sich dann aus den proportional bestimmten z seiner Teile zusammen, während die bez. des Hauptwertes geltenden Bestimmungen erhalten bleiben.]
§ 92. [Von diesen Formeln wird (26) im allgemeinen vorzuziehen sein. Denn (27) bezieht sich auf einen wenig interessierenden Hauptwert, dessen genaue Berechnung selbst schon nach Kap. X (19b) die Auflösung einer Gleichung zweiten Grades erfordert; während (25) dadurch im Nachteil steht, dasß A dem Lagengesetze gemäß von Dp durch C getrennt ist und somit, weniger häufig als C mit Dpim nämlichen Intervalle liegen wird. Es ist ferner nicht als Nachteil zu empfinden, daß die Gleichung (26) die Kenntnis der beiden Werte A und C erheischt, da man neben Dp stets auch A und C berechnen wird.]
[Es ist darum angezeigt, die auf die Kenntnis von C und A zu gründende Berechnung von Dpnach (26) auf eine möglichst einfache Form zu bringen.]
[Zu diesem Zwecke dividiere man (26) durch ¼ m²x und schreibe die Gleichung wie folgt:
![]() (28)
(28)
Setzt man nun:
so erhält man:
wodurch eine Kettenbruchdarstellung für x gegeben wird, die rasch konvergiert, da 2z0(C - A) : (Im) für unsere Tafeln kleine Werte darstellt.]
[Der Gang der Rechnung ist mithin der Art einzurichten, daß auf Grund von
![]() ;
;
![]() ;
;
etc.
![]() gleich
gleich ![]() .]
.]
[Aus der Gleichung (26) folgt überdies, daß von den empirisch bestimmten Hauptwerten A , C und Dp bei den für unsere Tafeln geltenden Größenverhältnissen das Lagengesetz von vornherein erfüllt wird. Bringt man nämlich jene Gleichung in die Form:
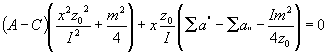 ,
,
![]() ,
,
daß A C und x , d. i. Dp C , weder gleichzeitig positiv, noch gleichzeitig negativ sein können. Es ist daher, da die angegebene Bedingung in der Tat von den Verteilungstafeln erfüllt wird,
wie das Lagengesetz es verlangt.]