![]() (1)
(1)
§ 76. Außer den im ganzen von mir bevorzugten drei Hauptwerten, dem arithmetischen Mittel A , dem Zentralwert C und dem dichtesten Wert D werden folgends noch drei nebensächlich von mir berücksichtigt werden, die ich als Scheidewert R , schwersten Wert T und Abweichungsschwerwert F aufführe.
Übersichtlich nach ihren Hauptunterschieden zusammengestellt, sind es folgende.
Scheidewert R , der Wert a , bezüglich dessen åa' = å a,= ½åa , mithin die Summe der größeren Werte gleich der Summe der kleineren und mithin jeder von beiden gleich der halben Gesamtsumme der a ist.
Arithmetisches Mittel A , der Wert a , bezüglich dessen åQ ' = åQ,, d. h. die Summe der positiven Abweichungen gleich der Summe der negativen ist; und bez. dessen åQ2ein Minimum ist.
Zentralwert C , der Wert a , bezüglich dessen m' = m,, d.h. die Zahl der positiven Abweichungen gleich der Zahl der negativen Abweichungen, und åQ ein Minimum ist.
Dichtester Wert D , der Wert a , bezüglich dessen sich die Abweichungszahlen beider Seiten m, : m' wie die mittleren Fehler derselben e,: e' verhalten, und die Maßzahl z ein Maximum ist.
Schwerster a-Wert T , der Wert a , dessen Maßprodukt za ein Maximum ist.
Abweichungsschwerwert F , der Wert a , bezüglich dessen zQein Maximum ist.
Ich werde jedoch diese Werte nicht in der vorigen Reihenfolge, sondern nach der Folge A , C , D , R , T , F behandeln.
Abgesehen von A sind die vorigen Werte wie die Werte des vorigen Kapitels einer rohen und scharfen Bestimmung fähig, indes bei A sich eine solche nicht unterscheiden läßt. Dieselbe kleine Verteilungstabelle wird hier wie dort zur Erläuterung der Ableitung dienen, und die dabei gebrauchten Bezeichnungen werden in dem, § 9 und 10 angegebenen Sinne zu verstehen sein. Bez. A gehen auch hier m,, m' , in µ,, µ' , und Q,,Q' in D,, D ' über.
§ 77. Arithmetischer Mittelwert A .
Der arithmetische Mittelwert einer Reihe von Werten a vereinigt folgende drei Eigenschaften in sich:
![]() (1)
(1)
Die vorigen Eigenschaften des A hängen so solidarisch zusammen, daß mit der einen zugleich die anderen gegeben sind, und er nach jeder derselben mit identischem Resultate abgeleitet werden kann, nur daß die Ableitung nach der ersten Eigenschaft die praktischste bleibt. Auch sind sie unabhängig von einem bestimmten Verteilungsgesetze der a und gelten über die Kollektivmaßlehre hinaus nicht bloß für eine als unendlich angenommene ideale, sondern auch jede endliche Reihe von a in willkürlicher Verteilung.åD2 = åD ' ² + åD,2= Minimum (3)
Der Zusammenhang des zweiten und dritten Satzes mit dem durch die Definition gegebenen ersten findet sich so.
Zweiter Satz. Jede positive Abweichung von A ist a' - A , jede negative nach absolutem Werte A - a,, hiernach entwickelt:
åD¢ = (a¢ A) + (a¢¢ A) +×××××× (4)
mithin, wenn µ' die Zahl der positiven, µ,die der negativen Abweichungen ist,åD,= (A a,) + (A a") + ×××××
åD¢ = åa¢ - µ¢ A
oder, weil åa ¢ + åa,= åa und µ¢ + µ,= m ,åD,= µ,A - åa,åD¢ - åD ,= åa¢ + åa,- (µ¢ + µ,) A (5)
åD¢ - åD,= åa m A , (6)
und weil A = åa
:
m
åD¢ - åD, = åa - åa = 0 (7)
Dritter Satz. Sei der Wert,
bez. dessen åD2
ein Minimum ist, zunächst als unbekannt = x gesetzt, so haben
wir:
Zwar sollte, sofern wir die negativen Abweichungen nach absolutem Werte als positiv nehmen, jede negative Abweichung statt a,- x u.s.w. vielmehr x - a, u.s.w. gesetzt werden; aber (a,- x)2 ist gleich (x - a,)2,was gestattet, den vorigen Wert von åD ² in angegebener Weise zu entwickeln. Nun erhalten wir den Minimumwert von åD2 durch Setzen des Differentials seines Ausdruckes bez. x gleich Null; dies gibt:åD ² = (a ¢ - x)² + (a¢¢- x)² + ×××× + (a,- x)² + (a"- x)² + ××××× (8)
mithin durch Summierung aller a und - x2[(a ¢ - x) + (a¢¢ - x) + ×××× + (a,- x) + (a"- x) + ××××× ] dx = 0 (9)
å a mx = 0 ,
. (10)
§ 78. Wenn schon der arithmetische
Mittelwert für die Kollektivmaßlehre nicht ein gleich überwiegendes
Interesse in Anspruch nehmen kann als für die physikalische und astronomische
Maßlehre, so gewährt ihm doch die Verbindung seiner drei Haupteigenschaften
auch für jene ein an sich mathematisches Interesse, was um so mehr
dadurch wächst, daß durch ihn eine Beziehung zwischen beiden
Lehren hergestellt wird. Gegen D steht er noch insbesondere durch
die größere Leichtigkeit und Einfachheit seiner genauen Bestimmung
im Vorteil; von C wird er darin zwar noch übertroffen, aber
daß in die Gleichheitsbestimmung seiner zweiten Eigenschaft mit der
Zahl zugleich die Größe der Abweichungen eingeht, gibt ihm ein
gewichtigeres Interesse als dem C . Auch läßt sich Folgendes
bemerken. Wenn man eine beliebige Reihe von a nach der zufälligen
Ordnung, wie sie in der Urliste enthalten sind, in eine gegebene Zahl Fraktionen
aus gleichviel a geteilt hat und aus jeder derselben das A besonders
bestimmt, so stimmt das arithmetische Mittel dieser A mit dem allgemeinen
Mittel der ganzen Reihe von a überein. Verfährt man aber
entsprechend mit der Bestimmung von C , so stimmt weder der Zentralwert,
noch Mittelwert der verschiedenen spezialen C allgemein gesprochen
mit dem aus der Totalität der a gewonnenen C überein.
Verfährt man entsprechend mit dem D , so stimmt zwar das D
, aber nicht der Mittelwert der spezialen D mit dem D der
Totalität der a überein.
Endlich knüpft sich an die Bestimmung von A folgender praktische Vorteil. Hat man das A eines K.-G. aus einer Verteilungstafel mit nicht zu kleinem m bestimmt, so wird man nicht nur die Gesamtgröße "Gr." des Gegenstandes für diese Tafel durch Multiplikation des A mit dem m , sondern auch nach Wahrscheinlichkeit die Gesamtgröße des Gegenstandes für jedes größere oder kleinere m durch Multiplikation jenes erst bestimmten A mit dem neuen m erhalten, nur mit einem um so größeren wahrscheinlichen Fehler dabei, je kleiner das m ist, und je weiter das m , auf das man schließt, von demselben abweicht. Umgekehrt wird man auf die Zahl von Exemplaren m , welche dazu gehört, eine gegebene Gesamtgröße Gr. zu geben, nach Wahrscheinlichkeit schließen können, indem man setzt m = Gr. : A ; da ja åa = mA = Gr. , mithin m = Gr. : A .
Diese Sätze können z. B. von Nutzen sein, wenn man den Raum bestimmen will, der eine gegebene Anzahl Menschen von zufällig wechselnder Größe faßt. Weder der Zentralwert, noch der dichteste Wert lassen eine entsprechende Verwendung zu.
§ 79. Es kann sein, daß man aus den A verschiedener K.-G. oder auch den besonders bestimmten A verschiedener Abteilungen desselben K.-G. ein gemeinsames Mittel ziehen will, und hat, wenn diese A aus verschiedenen m erhalten sind, zu unterscheiden, ob das definitive Mittel ohne oder mit Rücksicht auf die Verschiedenheit der m gezogen werden soll. Seien A1, A2 , A3 ... besondere Mittel, respektiv aus m1, m2, m3 ... Maßen gezogen. Ohne Rücksicht auf die Verschiedenheit der m wird das Mittel der betreffenden A sein:
![]() , (11)
, (11)
wo N die Anzahl der A ; mit Rücksicht auf die Verschiedenheit der m aber wird es sein:
![]() (12)
(12)
und mit dem Mittel übereinkommen, welches man erhält, wenn man die Gesamtsumme aller a mit der Gesamtsumme aller m dividiert.
Ersteres Mittel heiße das singuläre, letzteres das summarische. Je nach der Natur der Aufgabe kann die eine oder andere Art der Mittelziehung vorzuziehen sein. Gesetzt das Mittel aus der Körperlänge der Chinesen, Neger, Malaien, Amerikaner und Europäer kaukasischer Rasse soll bestimmt werden; aber von den Europäern liegen dazu 1000 Maße, von jeder der anderen Rassen nur 10 20 Maße vor; so würde die zweite, die summarische Art der Mittelziehung unzulässig sein; denn, wie leicht zu erachten, würde die mittlere Körperlänge dieser verschiedenen Rassen wegen des unverhältnismäßig überwiegenden Gewichtes, was die Europäer durch ihr großes m erhalten, fast ganz mit dem der Europäer übereinkommen, und überhaupt das definitive Mittel vorwiegend, durch das Spezialmittel mit dem größten m bestimmt werden, was der Natur der Aufgabe widerspricht. Hier ist nur die erste, die singuläre Art der Mittelziehung brauchbar; und daß nicht alle m dieselbe Größe haben, vermindert bloß die Sicherheit der Bestimmung gegen den Fall, daß die Gesamtheit der m sich gleich zwischen alle A verteilt. Überhaupt werden disparate Gegenstände (vgl. § 14) mehr Anlaß zur ersten als zweiten Mittelbestimmung geben; wogegen die Spezial-A aus verschiedenen Abteilungen eines einstimmigen Gegenstandes nach dem Prinzip der zweiten Mittelbestimmung zu kombinieren sind.
Es kann auch sein, daß man. statt aus verschiedenen A ein arithmetisches Mittel aus verschiedenen C oder D zu ziehen hat, und es gilt dann dafür die entsprechende Unterscheidung zwischen singulärem und summarischem Mittel, und gelten dieselben Gesichtspunkte der Bevorzugung des einen oder anderen.
§ 80. Zentralwert C .
Den drei Haupteigenschaften des arithmetischen Mittels A gegenüber vereinigt der Zentralwert C folgende drei Haupteigenschaften:
1. Die durch seine Definition gegebene Eigenschaft, ebensoviel größere a' über sich als kleiner a,unter sich zu haben.
2. Die Eigenschaft, gleich viel positive und negative Abweichungen von sich abhängig zu haben, so daß m' = m, = ½m .
3. Die Eigenschaft, daß die Summe der positiven und negativen Abweichungen von ihm nach absolutem Werte kleiner als von jedem anderen Werte, mithin bez. desselben åQ ein Minimum ist.
Auch diese Eigenschaften sind unter einander solidarisch und gelten für jede beliebige Reihe von a , rücksichtslos auf ein besonderes Verteilungsgesetz, entsprechend wie es von den drei Haupteigenschaften des A gilt.
Die Folgerung der zweiten Eigenschaft aus der ersten ist selbstverständlich und bedarf keiner Erläuterung.Der Zusammenhang der dritten damit aber folgert sich so.
Sei der Wert, von dem die dritte Eigenschaft gilt, zunächst als unbekannt = x gesetzt, so ist die Summe der Abweichungen bezüglich x nach absolutem Werte so anzusetzen:
m¢ = m,, (15)
was dem Begriffe des Zentralwertes entspricht.
Ich habe diese Eigenschaft des Zentralwertes zuerst in einer Abhandlung 1) über denselben bewiesen und durch Verallgemeinerung des Weges, welcher dazu führt, allgemeinere Folgerungen gezogen, auf die ich jedoch hier keinen Anlaß habe einzugehen.
1) [Über den Ausgangswert der kleinsten Abweichungssumme, dessen Bestimmung, Verwendung und Verallgemeinerung; Abhandlungen der math.-phys. Klasse der Kgl. Sächs. Gesellsch. d. Wissensch. XI. Band; 1878. S. l - 76.]
§ 81. Man kann dem Zentralwert folgende Bedeutung für die Kollektivmaßlehre beilegen.
Dächte man sich alle Exemplare eines K.-G. in eine große Urne getan, wofür man die Welt selbst ansehen kann, und nach Zufall ein Exemplar herausgezogen, so würde die Wahrscheinlichkeit gleich stehen, ein größeres und ein kleineres Exemplar als C herauszuziehen, und bei sehr vielen Zügen würde wirklich diese gleiche Wahrscheinlichkeit sich bewahren, wogegen bezüglich größerer Werte als C die Wahrscheinlichkeit des Herausziehens eines kleineren Gegenstandes, bezüglich kleinerer Werte als C die Wahrscheinlichkeit des Herausziehens eines größeren Exemplares überwiegt. Hiernach kann man C in demselben Sinne den wahrscheinlichen Wert eines K.-G. nennen, wie man den wahrscheinlichen Fehler eines Beobachtungsmittels so nennt, insofern die Wahrscheinlichkeit seiner Überschreitung und Unterschreitung gleich steht.
Bei der gemeinüblichen Weise, die Verteilungstafelm von K. G., namentlich Rekrutenmaßtafeln, so aufzustellen, daß von den Exemplaren, die unter und über eine gewisse Größengrenze gehen, nur die Zahl, nicht die Größensumme angegeben wird, fällt die Möglichkeit weg, ein genaues arithmetisches Mittel zu ziehen; und dann kann anstatt desselben der Zentralwert, welcher sich eben nach der bloßen Zahl bestimmen läßt, diesen, Vergleiche z. B. zwischen verschiedenen Jahrgängen und Örtlichkeiten, woher die Maße stammen, zu ziehen, ein Verfahren, was mir bei Bearbeitung langjähriger belgischer Rekrutenmaße aus den verschiedenen Provinzen Belgiens gedient hat, den Gang und Parallelismus diese Maße durch Zeit und Raum zu konstatieren.
§ 82. Die Herleitung des C aus einer Reihe von Werten a , die ihrer Größe nach geordnet sind, hat prinzipiell dadurch zu geschehen, daß man von jedem Ende der Reihe nach der Mitte zu gleichviel Werte abzählt und den Wert oder Zwischenwert zwischen zwei Werten als C nimmt, in dem beide Zählungen zusammentreffen, sofern hiermit dem Begriffe des C , nach beiden Seiten gleichviel Abweichungen und mithin gleichviel abweichende Werte über sich und unter sich zu haben, offenbar genügt ist. Es sind aber dabei zwei Fälle zu unterscheiden, erstens, wo das a , auf das man bei dieser doppelten Abzählung kommt, oder die zwei a , zwischen welchen das Resultat der Abzählung eintrifft, einfach sind, oder wo sie, wie im allgemeinen bei unseren Verteilungstafeln der Fall, mit einem z > 1 behaftet sind.
Fassen wir zunächst den ersten einfacher scheinenden Fall ins Auge. Für den ersten Anblick nun erscheint obige Regel hierbei darauf hinauszulaufen, daß man, wenn die Zahl der Werte m ist, ½m Werte, sei es von der einen oder anderen Seite her abzählt, und den ½m-ten Wert als C nimmt. Inzwischen überzeugt man sich leicht, daß diese Abzählung, je nachdem sie von der einen oder anderen Seite her geschieht, zu einem verschiedenen Werte fuhrt. Denn sei z. B. folgende Reihe von vier Werten:
Nehmen wir nun aber den zweiten, uns eigentlich allein interessierenden Fall, der bei unseren Verteilungstafeln stattfindet, daß die Zählung von beiden Seiten her in ein a eintrifft oder zwischen zwei a eintrifft, die mit einem z > 1 behaftet sind, so würden wir nach roher Bestimmung, indem wir diese z ganz auf die betreffenden a selbst fallend denken, auch das C erstenfalls mit jenem a selbst zusammenfallend oder zweitenfalls zwischen jene zwei a fallend und bei mangelndem bestimmten Anhalte als Mittel zwischen beiden zu nehmen haben. Und so hätte in unserer Beispielstabelle (§ 68) 11 als Zentralwert zu gelten, indem, wenn wir voriger Regel folgend ½ × 81 = 40½ von beiden Seiten abzählen, diese innerhalb des dem a = 11 zugeschriebenen z = 30 eintreffen.
Aber um eine schärfere Bestimmung zu erhalten, haben wir zu berücksichtigen, daß die z = 30 Exemplare sich durch das ganze Intervall von 10 bis 12 verteilen, und gelangen mit Rücksicht hierauf unter Zuziehung einer Interpolation dieses als I genommenen Intervalles zu einem übereinstimmenden C durch Abzählen von beiden Seiten her nicht von ½(m + 1), sondern von ½m Exemplaren, wie von vorn herein am natürlichsten erschien. In der Tat, um von oben herab (nach Lage der Tabelle) zum 40-sten (d. i. ½m-ten) Werte zu gelangen, haben wir zu berücksichtigen, (was sich unmittelbar in der Spalte der S,ablesen läßt) daß bis zu Ende des vorhergehenden Intervalles, mithin bis zu Anfang des I 18 Exemplare reichen; fehlen also zur Erfüllung der 40 noch 22 Exemplare, die ins Intervall I übergreifen. Nun schließen wir: wie sich diese ins Intervall übergreifenden 22 zur Totalzahl 30 des I verhalten, so der zum Anfang des I , d. i. zu 10 noch zuzufügende Wert x , sog. Eingriff in I , zur Größe von I , d. i. zu 2, mithin:
woraus sich der Zuwachs x zur ersten Grenze 10 wie oben = 1,467 bestimmt, was zu C = 11,467 zurückführt.30 (2 - x) = 16 ,
Da nun die zweite Bestimmungsweise nach ½m von unten herauf zu demselben Resultate führt als die erste, diese aber einfacher ist, so können wir uns zur Bestimmung von C bei dieser begnügen, und erhalten zur Bestimmung von C folgende Formel 2):
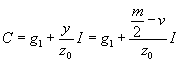 ,
(16)
,
(16)
wobei g1 wie früher den Anfangswert oder die erste Grenze des zu interpolierenden Intervalles, z0 das z dieses Intervalles, y den Zahleneingriff in dasselbe, d. h. die Zahl bedeutet, um welche die Vorzahl v noch vermehrt werden muß, um ½m zu gehen.
2 ) [Sollte an Stelle
der einfachen Interpolation die schärfere, unter Benutzung 2ter Differenzen,
treten, so müßte x = C - g1durch
Auflösen der Gleichung (16) des Kap. IX statt wie oben durch Auflösen
der Gleichung (13) ebendesselben Kapitels gewonnen werden.]
§ 83. Dichtester Wert D.
Definieren wir den dichtesten Wert zunächst kurz als den, der unter einer Reihe von a am häufigsten vorkommt, oder auf den das größte z fällt, so kann ein solcher Wert nicht wie die beiden vorigen Hauptwerte aus jeder beliebigen Reihe von a abgeleitet werden und hat überhaupt nur für die Kollektivmaßlehre eine in Betracht kommende, für sie aber sehr wichtige Bedeutung 3). In der Tat, stellen wir z. B. willkürlich folgende Reihe von fünf a auf:
3) Sollte freilich die bis jetzt nicht
beanstandete Annahme, daß die Beobachtungsfehler bei einwurfsfreien
Beobachtun-gen eine symmetrische W. bez. des arithmetischen Beobachtungsmittels
haben, irrig sein, so würde sich die große Wichtigkeit des D
auch auf die physikalische und astronomische Maßlehre erstrecken.
[Hierüber vergl. Kap. XXVIII.]
Daß bei symmetrischer W. der Abweichungen bez. A der dichteste Wert D wesentlich mit A und C zusammenfällt, ist mehrfach erwähnt; nach der Verallgemeinerung des G. G. für die asymmetrische W. der K.-G. aber weicht er allgemein gesprochen davon ab und besitzt dann keine von den drei Grundeigenschaften sei es des A noch des C ; hingegen die in § 33 aufgezählten Eigenschaften, wovon die wichtigsten solidarisch zusammenhängenden die sind: 1) daß er eben der dichteste im angegebenen Sinne ist, 2) daß das Proportionsgesetz, und 3) daß das zweispaltige G. G. bezüglich desselben besteht, wovon dann weiter abhängt, daß, um ein einfaches Verteilungsgesetz für Kollektivabweichungen zu gewinnen, die Abweichungen vielmehr von ihm, als von A oder C abhängig gemacht werden müssen. Man kann noch hinzufügen, daß D den wahrscheinlichsten Wert eines K.-G. aus folgendem Gesichtspunkte darstellt.
Greift man aus der Gesamtheit der a eines K.-G. ein Exemplar nach Zufall heraus, so wird der Wert D wahrscheinlicher als jeder andere getroffen werden, und die ihm nahen a mit einer, der seinigen nahe gleich kommenden, doch verschiedenenW., je nachdem sie auf die eine oder andere Seite von D fallen.
Hiernach überbietet die Wichtigkeit des D für K.-G. aus mehr als einem Gesichtspunkte die jedes anderen Hauptwertes, ohne jedoch damit zu hindern, daß diese nach den Eigenschaften, welche er nicht mit ihnen teilt, beachtenswert bleiben und zur vollständigen Charakteristik eines K.-G. gehören; auch steht er insofern im Nachteile gegen alle anderen, daß seine möglichst genaue Darstellung umständlich ist und eine Rechenarbeit fordert, deren es für die anderen nicht bedarf. Hierauf wäre nun näher einzugehen; aber ich verspare lieber die ziemlich umständlichen Erörterungen über seine Ableitung überhaupt auf ein besonderes Kapitel, um noch die folgenden drei Hauptwerte zu besprechen.
§ 84. Scheidewert R.
Der Wert, der eine gleiche Summe von a über sich als unter sich hat, und welcher also die Scheidegrenze zwischen den ihrer Größe nach geordneten kleineren und größeren a zu bilden hat, wenn durch Summierung der kleineren a dieselbe Gesamtgröße erzeugt werden soll, als durch Summierung der größeren a .
[Er liegt oberhalb C . Denn die Anzahl der oberhalb und unterhalb C gelegenen a ist beidesfalls, dem Begriffe des C gemäß, gleich ½m ; es ist daher:
![]() ,
,
so daß eine Gleichheit der unteren mit der oberen Summe nur für einen Wert, der größer als C ist, erreicht werden kann. Er liegt somit zugleich oberhalb A oder oberhalb D ; je nachdem A oder D kleiner als C ist, wogegen er möglicherweise unterhalb des einen oder des anderen dieser beiden Hauptwerte liegen kann, wenn der eine oder der andere größer als C ist. Um jedoch seine Lage zunächst mit Rücksicht auf das in der Regel als bereits bekannt vorauszusetzende A zu bestimmen, werde angenommen, daß R oberhalb A liege.]
Seien nun åa,, åa' die Summen unterhalb und oberhalb R , å a" und åa" die Summen unterhalb und oberhalb A , so zähle man s = ½ (åa" - å a") nach oben, d. i. nach den größeren Werten zu von A ab, um zu R zu gelangen.
Beweis. Nach Anschauung des
Linienschemas
¾¾¾¾¾¾¾¾|¾¾¾¾¾¾|¾¾¾¾¾¾¾¾
A R
ist die untere Summe der a bez. R gleich der unteren Summe bez. A plus der Summe zwischen A und R , welche sheiße, d. i.
also, da
åa" = µ¢ A + åD ' ,
![]() (18)
(18)
Diese Bestimmungsweisen gelten rücksichtslos auf ein besonderes Verteilungsgesetz, nur daß eine rohe und scharfe Bestimmung dabei in gewohnter Weise unterschieden werden kann. [Sie behalten ihre Geltung auch für den Fall, daß A oberhalb R liegt; swird jedoch alsdann negativ und ist daher, seinem absoluten Werte nach genommen, nach unten d. i. nach den kleineren Werten zu von A abzuzählen, um zu R zu gelangen.]
In unserem Erläuterungsbeispiel ist nach früherer Bestimmung A = 11,4; åa"= 369; åa" = 543, mithin unser jetziges ? = 87; diese Summe haben wir von 11,4 an aufwärts, d. i. nach den größeren a zu, zu zählen, um zu R zu gelangen und dazu das Intervall 10 12 mit za = 330 zu interpolieren, was dazu führt, 2 × 87 : 330 = 0,527 zu 11,4 zu fügen; gibt R = 11,927. [Setzt man jedoch wie früher (§ 72) å'a" = 362,7 ; å' a" = 549,3 , mithin s = 93,3 , so ist konsequenterweise die Differenz R A = x aus der Gleichung: 93,3 = (11,4 + ½x) ×15x mit dem Werte 0,533 zu finden; gibt mit obigem Werte wesentlich übereinstimmend R = 11,933.]
[Statt nun, wie hier geschehen, R in Abhängigkeit von A zu bestimmen, kann es ganz ebenso in Abhängigkeit von C oder von D gefunden werden; dann sind natürlich åa", å a" und entsprechend die Abweichungszahlen und Abweichungssumme bez. C oder D statt bez. A zu nehmen. Man erhält so beim Ausgange von C die Bestimmung: s = ½åQ (bez. C); beim Ausgange von D dagegen: s = ½(m' m,) D + ½ å¶ . Überdies kann R auch direkt, ohne Anlehnung an einen vorbestimmten anderen Hauptwert gefunden werden. Es geschieht dies, indem man durch Addieren der a von beiden Enden der Verteilungstafel das Intervall aufsucht, in welches R zu liegen kommt, und dann in diesem Eingriffsintervall die Eingriffssumme Y der Art bestimmt, daß die Vorsumme vermehrt um die Eingriffssumme gleich der halben Gesamtsumme der a ist. Dies führt, unter Benutzung der (§ 69) definierten Bezeichnungen, zu der Formel:
![]() (19a)
(19a)
oder zu
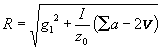 ,
(19b)
,
(19b)
je nachdem, im Einklange mit den § 72 getroffenen Bestimmungen, das Eingriffsmaß x , d. i. der Wert, um welchen R die untere Grenze g1 des Intervalles I überragt, nach der Proportion
x : I = Y : a0z0
oder genauer nach der Gleichung:
![]()
berechnet und zu g1 hinzugefügt wird.]
[Schließlich verdient noch erwähnt
zu werden, daß die Lage von R in anderer Weise als diejenige
von A , C und D von den a der Verteilungstafel abhängt.
Vermehrt man nämlich jedes a um einen und denselben Betrag,
so wird auch A , C und D um den nämlichen Betrag größer,
so daß die Lage innerhalb der Tafel erhalten bleibt; dagegen bewirkt
die angegebene Vermehrung eine Annäherung des R an C
der Art, daß bei unbegrenzter Vermehrung R mit C zusammenfällt.
Dies folgt unmittelbar daraus, daß die zwischen C und R
gelegene
Summe der a , d. i. s, beständig
gleich ½åQ (bez.
C) ist
und sich somit bei größer werdenden a auf ein immer kleiner
werdendes Intervall verteilt.]
§ 85. Der schwerste Wert T .
Jeder Wert a einer zu unseren Untersuchungen tauglichen Verteilungstafel gibt, allgemein gesprochen, je nach seiner Größe und dem z , wie oft er vorkommt, ein verschiedenes Produkt za ,und man kann nun nach dem a fragen, für welches dieses Produkt ein Maximum ist. Zunächst läßt sich daran denken, daß es mit dem dichtesten Werte zusammenfalle. Aber bei diesem kommt es bloß auf die Größe des z , nicht des za an. Es gibt Werte a , die größer sind als D , und obwohl sie seltener vorkommen als D , gibt ihnen doch bis zu gewissen Grenzen die Größe des a betreffs des za , was sie liefern, einen Vorteil.
In jedem Falle kann T bloß nach positiver Seite von D abliegen, weil beim Herabgehen der Werte a unter D sowohl a als z abnehmen. Nach roher Bestimmung würde in unserer Beispielstabelle T mit D zugleich auf a = 11 fallen, sofern sich hierfür das Maximal-za = 330 findet. Nach scharfer Bestimmung aber fallen beide aus einander, und hat man dazu, wenn das zweiseitige G. G. als zutreffend vorausgesetzt wird, nach unten folgendem Beweise überhaupt folgende Formel zu benutzen:
![]() . (20)
. (20)
Aus unserer Beispielstabelle § 68 findet sich nach dem im nächsten Kapitel auseinander zu setzenden Proportionsverfahren
[Dies findet sich nun aber nicht bestätigt; denn das za des Intervalles 11,1 13,1 ist gleich 296, während das za des Intervalles 10 12 gleich 330 ist. Dadurch wird jedoch nicht die Unrichtigkeit der obigen theoretischen Bestimmungsweise von T nachgewiesen, sondern nur nahe gelegt, daß die theoretisch geforderte Lage des schwersten Wertes nicht mit seiner, in der Tafel empirisch dargebotenen Lage genau übereinstimmt, was übrigens von vornherein nicht anders zu erwarten ist. Daß dies auch bei den Tafeln empirisch gegebener K.-G. nicht wesentlich anders ist, erhellt aus folgendem Beispiel.]
Die Verteilungstafel für den vertikalen Schädelumfang mit i = 5 mm (§ 58) gibt nach Bestimmung des D mittelst des Proportionsverfahrens:
Da die za der betreffenden Intervalle
in der Verteilungstafel nicht unmittelbar gegeben sind, weil diese Intervalle
selbst mit ihren
za
nicht darin gegeben sind, vielmehr das Intervall
des schwersten Wertes, ebenso wie das des dichtesten Wertes, zwischen zwei
Intervalle der gegebenen Tafel übergreift, so muß man interpolationsmäßig
berechnen, welchen Anteil zum gesuchten za jedes beider Intervalle
liefert, und durch Summierung dieser Anteile sowohl das za des Intervalles,
was für D , als was für T einzustellen hat, finden,
was ich hier nicht detaillieren will 4).
Hiernach fand ich für obiges Beispiel das za des dichtesten
Wertes 26631, das des T
gleich 26656, also, wie zu erwarten, das
letztere sehr wenig, aber, wie zu verlangen, doch etwas größer
als das erstere. [Aber trotzdem ist das theoretisch aus (20) bestimmte
T von dem empirisch aus der Tafel zu entnehmenden verschieden; denn
für a = 413 ergibt sich der noch größere Wert za
= 26845.]
4) [In dem vorliegenden
Falle vereinfacht sich infolge des für a = 408 und a = 413
gemeinsamen z = 65 diese Rechnung, und findet man das za für
D resp. T
gleich 65. D resp. 65. T.]
setzen, diesen Wert zur Erlangung einer Maximumgleichung in Bezug auf ¶ differenzieren und das Differential gleich Null setzen, wobei wir einfachheitshalber die Strichelchen oben an z , a , ¶, e weglassen, die eigentlich anzubringen sind, um die Lage dieser Werte oberhalb D zu bezeichnen.za = z(D +¶ ) (22)
![]() , (23)
, (23)
![]() , (24)
, (24)
worin h = 1 : e![]() .
Bei dem normaler Weise vorauszusetzenden großen m aber kann
j¶
auch durch z : m'
ausgedrückt
werden, mithin
.
Bei dem normaler Weise vorauszusetzenden großen m aber kann
j¶
auch durch z : m'
ausgedrückt
werden, mithin
![]() , (25)
, (25)
woraus folgt:
![]() (26)
(26)
und, weil ![]()
![]() ,
(27)
,
(27)
also:
![]() ,
(28)
,
(28)
worin z als gemeinsamer Faktor wegfällt, und
man mit Umkehrung der Vorzeichen und Rücksicht, daß h
= 1 : e ![]() ,
folgende quadratische Gleichung erhält:
,
folgende quadratische Gleichung erhält:
2¶ ² + 2D¶- pe² = 0, (29)
aus der sich ¶ bestimmen läßt.
Dies gibt zunächst:
![]() ,
(30a)
,
(30a)
wovon bloß das obere Vorzeichen brauchbar ist; oder:
![]() (30b)
(30b)
und:
![]() (31)
(31)
§ 86. Abweichungsschwerwert F .
Man kann noch von einem charakteristischen Abweichungswerte sprechen, welcher dem schwersten a-Werte analog ist und analog zu berechnen ist, hiernach der schwerste Abweichungswert heißen kann. Dort fragte man, auf welches a fällt das größte za , hier fragt man, auf welches Q fällt das größte zQ , und sofern bei Ausgang von einem gegebenen Hauptwerte H mit Q zugleich a = H ± Q gegeben ist, auf welches a fällt das größte zQ , ein Wert, der keineswegs mit dem schwersten a-Werte zusammenfällt. Inzwischen schlägt die Analogie in folgenden Punkten fehl. Das Maximum von za ist unabhängig von dem Hauptwerte, den man etwa bevorzugen will, da dieser ja an den faktischen Werten der a und darauf bezogenen z nichts ändert, nur daß eine einfache Berechnung des größten za bloß unter Ausgang von D nach unserem allgemeinen Verteilungsgesetze möglich ist. Hiergegen hängt der Wert zQ mit von dem Hauptwerte ab, von dem an man die Abweichungen rechnen will, da die Werte Q selbst ihrer Größe nach davon abhängen. Es bleibt sich aber mit der Berechnung des schwersten a-Wertes gleich, daß sie auch bei dem schwersten Q -Wert nur im Ausgange von D unter Zugrundelegung unseres allgemeinen Verteilungsgesetzes geschehen, und das Zutreffen des Resultates durch mangelnde Erfüllung der Requisiten gestört werden kann. Endlich hält die Analogie insofern nicht Stich, als es normaler Weise nur ein Maximum von za' in jeder Verteilungstafel geben kann; wogegen es für jede Seite des gewählten Hauptwertes ein besonderes Maximum von zQ resp. von z'Q ' und z,Q,kurz F' und F, gibt, was eben bei Ausgang von D einer ganz entsprechenden Berechnung unterliegt.
Zur Erläuterung nehmen wir die reduzierte Tabelle für den Vertikalumfang des Schädels (§ 58) mit E, = 368 ; i = 5 , wofür nach § 61:
| a, | ¶, | z, | z,¶ , |
| 383 | 26,7 | 17 | 454 |
| 388 | 21,7 | 24 | 521 |
| 393 | 16,7 | 36 | 601 |
| 398 | 11,7 | 41 | 480 |
| 403 | 6,7 | 59 | 395 |
| 405,5 D | 0 4,2 | 55 | 115 |
| a' | ¶' | z¢ | z'¶ ' |
| D 410,5 | 0 0,8 | 10 | 4 |
| 413 | 3,3 | 65 | 214 |
| 418 | 8,3 | 51 | 423 |
| 423 | 13,3 | 40 | 532 |
| 428 | 18,3 | 17 | 311 |
Man sieht hier, daß ¶ und z insofern einen umgekehrten Gang nehmen, als ¶ mit Annäherung seiner a an D auf jeder Seite abnimmt, z wächst; umgekehrt bei Entfernung der a von D . Sollten nun z und ¶ hierbei ein umgekehrtes Verhältnis befolgen, so würde z¶ durch die ganze Reihe der Werte konstant bleiben, was aber keineswegs der Fall ist, wie man sich aus der letzten Spalte überzeugen kann, wonach für die a,-Seite ein Maximum von z,¶ ,, kurz F,, bei ¶,= 16,7 und a,= D - ¶,= 393 ; und auf der a'-Seite ein Maximum von z'¶ ' , kurz F' , bei ¶¢= 13,3 und a' = D + ¶' = 423 stattfindet. [Die nämlichen Werte markieren auch bei scharfer Bestimmung mittelst einfacher Interpolation die Maxima der z¶.]
Wie man nun sieht, stimmt der so empirisch
bestimmte Maximumwert von z,¶
,=F, sehr nahe mit dem oben
angegebenen Werte e,![]() =
14,9 und der empirisch gefundene Maximumwert von z'¶
' = F' auf der a'-Seite sehr nahe mit dem oben angegebenen Werte
e'
=
14,9 und der empirisch gefundene Maximumwert von z'¶
' = F' auf der a'-Seite sehr nahe mit dem oben angegebenen Werte
e'![]() =
13,0 ; und in der Tat ist das Resultat der nachher zu begründenden
Rechnung auf Grund der Gültigkeit unseres Verteilungsgesetzes, daß
=
13,0 ; und in der Tat ist das Resultat der nachher zu begründenden
Rechnung auf Grund der Gültigkeit unseres Verteilungsgesetzes, daß
![]() ;
; ![]() (32)
(32)
[Bestimmt man aber interpolationsmäßig die den Werten ¶,=14,9 und ¶' = 13,0 zugehörigen z,¶, und z'¶' mit Rücksicht, daß i = 5, so findet, man z,¶ ,= 563 ; z¢¶ ' = 529, deren Vergleich mit den wirklichen Maximalwerten der Tafel den Grad der Übereinstimmung zwischen den theoretisch geforderten und empirisch dargebotenen Werten erkennen läßt.]
[Beweis. Setzt man auf Grund des als gültig vorauszusetzenden zweispaltigen G. G.:
![]() , (33)
, (33)
wo h' = 1 : e'![]() ,
so ist zur Erlangung der Maximumgleichung für z' ¶
' der Wert:
,
so ist zur Erlangung der Maximumgleichung für z' ¶
' der Wert:
![]() (34)
(34)
in Bezug auf ¶' zu differenzieren und das Differential gleich Null zu setzen. Man erhält so:
![]() , (35)
, (35)
also, da der Koeffizient von ( 1 - 2h'² ¶ '² ) seiner Natur nach nicht verschwinden kann,
![]() oder
oder ![]() .
(36)
.
(36)
In gleicher Weise folgt für die unteren Abweichungen:
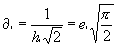 .
(37)
.
(37)
Es sind nun aber e'![]() und
e,
und
e,![]() die beiderseitigen mittleren quadratischen Abweichungen, so daß die
theoretische Bedeutung der Abweichungsschwerwerte F' und F,
bezüglich
D
eben
darin besteht, die quadratische mittlere Abweichung der oberen und der
unteren Werte darzustellen.]
die beiderseitigen mittleren quadratischen Abweichungen, so daß die
theoretische Bedeutung der Abweichungsschwerwerte F' und F,
bezüglich
D
eben
darin besteht, die quadratische mittlere Abweichung der oberen und der
unteren Werte darzustellen.]