§ 47. [In den vorhergehenden Kapiteln wurden die Hauptpunkte der Untersuchung vorgreiflich dargelegt. Jetzt gilt es, die Untersuchung tatsächlich zu führen. Da dieselbe nicht auf hypothetischen Annahmen fußt; sondern völlig auf die Erfahrung sich gründet, so kann sie nur von den empirisch gegebenen K.-G. selbst ausgehen. Die letzteren sind aber in ihrer usprünglichen Form weder zur Ableitung, noch zur Bewährung der theoretisch gültigen Gesetze geeignet. Es muß daher vor allem ihre rechnerische Behandlung gelehrt werden. Dieselbe befaßt sich einesteils mit der Herstellung einer zur Untersuchung tauglichen Darstellungsform durch Aufstellung primärer und reduzierter Verteilungstafeln (Kap. VII und VIII); anderenteils gibt sie Regeln zur Berechnung der Hauptwerte und Abweichungsfunktionen, in welchen die charakteristischen Merkmale und Eigenschaften der K.-G. sich darbieten (Kap. IX - XI). Hierbei wird einfachheitshalber bloß von der arithmetischen Behandlung der K.-G. die Rede sein; denn die logarithmische Behandlung, mit welcher erst die volle Allgemeinheit der Untersuchungsmethode erreicht wird, stimmt mit der arithmetischen der Hauptsache nach überein, indem nur die Logarithmen der Maße an Stelle der Maße selbst treten.]
[Ist nun hiermit eine geeignete Unterlage für die theoretische Untersuchung gewonnen, so bietet sich zunächst die Aufgabe dar, die Asymmetrie der K.-G. zu erörtern und Kriterien zur Unterscheidung wesentlicher und unwesentlicher Asymmetrie aufzustellen (Kap. XII - XVI). Dann aber sind die bei wesentlicher Symmetrie und wesentlicher Asymmetrie gültigen Veteilungsgesetze zu entwickeln (Kap. XVII - XX). Dabei wird der in der Regel stattfindende Fall geringer verhältnismäßiger Schwankung der Einzelwerte um die Hauptwerte vorausgesetzt.]
[Diesem Hauptteile der Untersuchung schließt sich die Besprechung der Modifikationen an, die durch den Übergang zum logarithmischen Verteilungsgesetz bedingt werden. Eine logarithmische Behandlung erfordern in erster Linie die K.-G. mit starker verhältnismäßiger Schwankung, aber auch die Verhältnisse zwischen den verschiedenen Dimensionen der K.-G. bedürfen einer solchen (Kap. XXI und XXII). Anhangsweise werden schließlich die Abhängigkeitsverhältnisse der K.-G. erörtert (Kap. XXIII).]
§ 48. [Will man einen K.-G. in Untersuchung nehmen, so sind zunächst die einzelnen Exemplare desselben in der zufälligen, räumlichen oder zeitlichen Ordnung, in der sie sich darbieten, zu messen und die mit a zu bezeichnenden Maße in einer Urliste zu verzeichnen. Hierbei ist darauf zu achten, daß die in Kap.IV angegebenen Requisiten erfüllt werden, also insbesondere eine genügende Anzahl von Maßen unter Ausschluß von Abnormitäten zusammengebracht wird.]
[Eine solche Urliste ist, wie bereits (§ 3) bemerkt wurde, zur rechnerischen Behandlung noch nicht geeignet. Sie ist jedoch in anderer Hinsicht wertvoll, da sie die Feststellung ermöglicht, ob die Exemplare der K.-G. unabhängig von einander variieren oder in einem Abhängigkeitsverhältnisse stehen. Diesbezüglich wurden in § 20 Regeln angegeben, die in Kap. XXIII eine weitere Ausführung erhalten werden. Im Interesse der rechnerischen Behandlung aber muß man die Maße ihrer Größe nach ordnen und hiermit aus der Urliste eine Verteilungstafel herstellen. Sie wird zur Unterscheidung von der reduzierten Tafel, deren Herstellung und Behandlung im nächsten Kapitel gelehrt wird, primäre Verteilungstafel genannt. In derselben bilden die Maße a eine von den kleineren zu den größeren Werten fortschreitende Kolumne, die jedes a nur einmal enthält, während eine beigegebene Kolumne die zugehörigen Anzahlen z aufführt, die angeben, wie oft jedes einzelne a vorkommt.]
[Diese primäre Tafel bildet nun den Ausgangspunkt der ganzen Untersuchung. Sie ist jedoch meist noch mit starken Unregelmäßigkeiten behaftet und besitzt gewöhnlich eine solche Ausdehnung, daß ihre Mitteilung einen zu großen Raum beanspruchen würde. Man wird darum beiden Nachteilen durch Vornahme von Reduktionen zu begegnen suchen und dann im allgemeinen auf die Vorführung der Tafel in ihrer reduzierten Form sich beschränken. Hier handelt es sich aber darum, die Beschaffenheit der primären Tafeln kennen zu lernen und einen Einblick in die möglicherweise auftretenden Besonderheiten zu gewinnen; es sollen deshalb von vier, als Beispiele dienenden K.-G. die primären Tafeln vorgeführt werden.]
§ 49. [Die beiden ersten Tafeln
I und II geben die Maße für den Vertikal- und Horizontalumfang
von 450 europäischen Männerschädeln. Dabei ist zu bemerken,
daß die hier und im folgenden durchweg festgehaltene Bezeichnung
"Vertikalumfang" genauer durch "Länge des Scheitelbogens" zu ersetzen
wäre, indem nicht der totale Umfang, sondern nur der über Stirn,
Scheitel und Hinterhaupt bis zum Vorderrande des Markloches sich erstreckende
Bogen, mithin der um die Schädelbasis verminderte Vertikalumfang in
der Tabelle angegeben wird. Wie bereits im III. Kapitel bemerkt, wurden
die Maße von Prof. WELCKER zur Verfügung gestellt, der ein reichhaltiges,
gleichmäßig behandeltes Material unter Festhalten eines und
desselben Messungsverfahrens gesammelt hat.1)
Die Maßeinheit ist das Millimeter. Zur
Messung diente ein Bandmaß. Die Maße selbst beziehen sich nach
WELCKER’s Angabe auf "normale" männliche Schädel. Schädel
mit Nahtabnormitäten, selbst Stirnnahtschädel wurden ausgeschlossen.]
1) [Vergl. H. WELCKER, Wachstum und Bau
des menschlichen Schädels, Leipzig 1862; ferner: Die Kapazität
und die drei Hauptdurchmesser der Schädelkapsel bei den verschiedenen
Nationen; Archiv für Anthropologie, Bd. XVI].
[Tafel III enthält die Rekrutenmaße von 2047 zwanzigjährigen Leipziger Studenten aus den 20 Jahrgängen 1843 - 1862. Von der Urliste dieser Maße ist zu bemerken, daß sie durch eine in ihrer Herstellungsweise beim Aushebungsgeschäfte begründete, reine Zufälligkeit in der Folge der Maßgrößen ausgezeichnet ist, weshalb dieselbe in Kap. XX zur Bewährung der Extremgesetze verwendet wird. Die Maßeinheit ist der sächsische Zoll = 23,6 mm; es wurden jedoch nicht nur die ganzen, sondern auch halbe und viertel Zoll gemessen.]
[In Tafel IV sind die Maße für das oberste Glied (Internodium) von 217 sechsgliedrigen Roggenhalmen verzeichnet. Genauere Angaben über die Gewinnung dieses Materiales finden sich im zweiten Teile, Kap. XXV. Mit dem eben dort beschriebenen Messungsverfahren hängt es zusammen, daß als Maßeinheit das halbe Zentimeter auftritt.]
§ 50. [Die vier Tafeln lauten der Reihe nach:2)]
Tafel I. 450 europ. Männerschädel; Vertikalumfang.
E = 1 mm; m = åz = 450; A1 = 408,5.
| a | z | a | z | a | z | ||
| 368 |
1
|
400 |
13
|
425 |
8
|
||
| 371 |
2
|
401 |
12
|
426 |
7
|
||
| 376 |
1
|
402 |
13
|
427 |
3
|
||
| 378 |
1
|
403 |
6
|
428 |
4
|
||
| 379 |
1
|
404 |
10
|
430 |
3
|
||
| 380 |
2
|
405 |
18
|
431 |
3
|
||
| 381 |
1
|
406 |
8
|
432 |
2
|
||
| 382 |
2
|
407 |
8
|
433 |
5
|
||
| 383 |
3
|
408 |
16
|
434 |
5
|
||
| 384 |
3
|
409 |
13
|
435 |
4
|
||
| 385 |
8
|
410 |
20
|
438 |
1
|
||
| 386 |
2
|
411 |
9
|
440 |
3
|
||
| 387 |
6
|
412 |
15
|
442 |
1
|
||
| 388 |
4
|
413 |
8
|
443 |
1
|
||
| 389 |
5
|
414 |
12
|
447 |
1
|
||
| 390 |
7
|
415 |
21
|
448 |
1
|
||
| 391 |
7
|
416 |
6
|
||||
| 392 |
7
|
417 |
5
|
||||
| 393 |
2
|
418 |
16
|
||||
| 394 |
8
|
419 |
9
|
||||
| 395 |
12
|
420 |
15
|
||||
| 396 |
4
|
421 |
8
|
||||
| 397 |
7
|
422 |
7
|
||||
| 398 |
14
|
423 |
5
|
||||
| 399 |
3
|
424 |
12
|
2) [Da weder die Urlisten, noch die primären Tafeln der hier behandelten K.-G. sich vorfanden (vergl. Anmerkung zu Kap. III), so mußten die obigen Tafeln rekonstruiert werden. Tafel I und III konnten aus den fünf resp. vier Reduktionslagen, die im folgenden Kapitel (§ 64 und 65) verzeichnet sind, wieder hergestellt werden, für Tafel II und IV lagen die entsprechenden Bearbeitungen nicht in hinreichender Vollständigkeit vor. Indessen fanden sich für Tafel IV die Logarithmen der a-Werte. Die Werte der Tafel II dagegen wurden aus den von Prof. WELCKER mir übermittelten Maßen von 500 europäischen Männerschädeln gewonnen. Dabei mußten aber 63 Maße nach ihrer wahrscheinlichen Zugehörigkeit zu den entsprechenden Vertikalmaßen ergänzt werden, da nur so eine Übereinstimmung mit der reduzierten Tafel des folgenden Kapitels (§ 58) erzielt werden konnte. Die hierdurch möglicherweise bedingten, geringfügigen Abweichungen beeinträchtigen jedoch das Bild der Tafel nicht, die überdies im folgenden nicht wesentlich in Betracht kommt.]
Tafel II. 450 europ. Männerschädel; Horizontalumfang.
E = 1 mm; m = åz, = 450; A1 = 522,2.
| a | z | a | z | a | z | ||
| 481 |
1
|
510 |
13
|
535 |
10
|
||
| 484 |
2
|
511 |
12
|
536 |
11
|
||
| 485 |
2
|
512 |
14
|
537 |
5
|
||
| 486 |
1
|
513 |
7
|
538 |
8
|
||
| 488 |
1
|
514 |
6
|
539 |
9
|
||
| 489 |
2
|
515 |
13
|
540 |
14
|
||
| 490 |
2
|
516 |
11
|
541 |
6
|
||
| 491 |
1
|
517 |
7
|
542 |
3
|
||
| 492 |
1
|
518 |
9
|
543 |
4
|
||
| 493 |
2
|
519 |
10
|
544 |
3
|
||
| 494 |
4
|
520 |
15
|
545 |
4
|
||
| 495 |
5
|
521 |
6
|
546 |
3
|
||
| 496 |
1
|
522 |
8
|
547 |
2
|
||
| 497 |
4
|
523 |
14
|
548 |
2
|
||
| 498 |
1
|
524 |
17
|
549 |
3
|
||
| 499 |
2
|
525 |
2 1
|
550 |
6
|
||
| 500 |
8
|
526 |
9
|
552 |
1
|
||
| 501 |
4
|
527 |
8
|
553 |
1
|
||
| 502 |
3
|
528 |
7
|
554 |
4
|
||
| 503 |
6
|
529 |
8
|
555 |
2
|
||
| 504 |
9
|
530 |
13
|
558 |
1
|
||
| 505 |
8
|
531 |
5
|
561 |
1
|
||
| 506 |
4
|
532 |
6
|
567 |
2
|
||
| 507 |
3
|
533 |
7
|
576 |
1
|
||
| 508 |
6
|
534 |
8
|
||||
| 509 |
7
|
Tafel III. Studentenrekrutenmaße.
E = 1 Zoll,
m
= å z = 2047; A1
= 71,77.
| a | z | a | z | a | z | ||
| 60,00 |
1
|
70,00 |
70
|
76,00 |
24
|
||
| 64,00 |
2
|
70,25 |
65
|
76,25 |
17
|
||
| 64,75 |
4
|
70,50 |
71
|
76,50 |
9
|
||
| 65,00 |
6
|
70,75 |
61
|
76,75 |
7
|
||
| 65,25 |
3
|
71,00 |
78
|
77,00 |
14
|
||
| 65,50 |
5
|
71,25 |
75
|
77,25 |
9
|
||
| 65,75 |
5
|
71,50 |
81
|
77,50 |
7
|
||
| 66,00 |
8
|
71,75 |
89
|
77,75 |
3
|
||
| 66,25 |
6
|
72,00 |
79
|
78,00 |
3
|
||
| 66,50 |
9
|
72,25 |
81
|
78,25 |
2
|
||
| 66,75 |
19
|
72,50 |
82
|
78,50 |
3
|
||
| 67,00 |
7
|
72,75 |
63
|
79,00 |
1
|
||
| 67,25 |
11
|
73,00 |
79
|
79,50 |
2
|
||
| 67,50 |
25
|
73,25 |
79
|
80,00 |
1
|
||
| 67,75 |
15
|
73,50 |
68
|
80,75 |
1
|
||
| 68,00 |
35
|
73,75 |
56
|
82,50 |
1
|
||
| 68,25 |
27
|
74,00 |
64
|
||||
| 68,50 |
37
|
74,25 |
42
|
||||
| 68,75 |
34
|
74,50 |
55
|
||||
| 69,00 |
43
|
74,75 |
33
|
||||
| 69,25 |
48
|
75,00 |
43
|
||||
| 69,50 |
57
|
75,25 |
26
|
||||
| 69,75 |
54
|
75,50 |
25
|
||||
| 75,75 |
17
|
Tafel IV. Das oberste Glied von 217 sechsgliederigen Roggenhalmen.
E = 0,5 cm; m = å z = 217; A1= 86,54.
| a | z | a | z | a | z | a | z | a | z | ||||
| 42,9 | 1 | 75,6 | 1 | 85,4 | 1 | 91,7 | 1 | 99,0 | 2 | ||||
| 49,7 | 1 | 75,8 | 2 | 85,5 | 1 | 91,9 | 2 | 99,2 | 1 | ||||
| 52,8 | 1 | 76,1 | 1 | 85,7 | 1 | 92,0 | 2 | 99,3 | 1 | ||||
| 55,6 | 1 | 76,2 | 2 | 85,8 | 1 | 92,3 | 1 | 99,4 | 1 | ||||
| 57,6 | 1 | 76,4 | 2 | 85,9 | 1 | 92,8 | 1 | 99,5 | 1 | ||||
| 58,9 | 1 | 76,7 | 1 | 86,0 | 2 | 93,0 | 2 | 100,3 | 1 | ||||
| 59,0 | 1 | 77,0 | 1 | 86,2 | 1 | 93,1 | 1 | 100,5 | 1 | ||||
| 61,4 | 1 | 77,2 | 1 | 86,3 | 1 | 93,3 | 1 | 100,8 | 1 | ||||
| 61,9 | 1 | 77,5 | 1 | 86,8 | 2 | 93,4 | 1 | 100;9 | 1 | ||||
| 62,2 | 1 | 77,6 | 1 | 86,9 | 1 | 93,5 | 2 | 101,0 | 1 | ||||
| 62,3 | 1 | 77,7 | 1 | 87,0 | 3 | 93,7 | 1 | 101,1 | 1 | ||||
| 63,0 | 1 | 77,9 | 1 | 87,1 | 2 | 94,4 | 1 | 101,3 | 1 | ||||
| 64,1 | 1 | 78,0 | 1 | 87,4 | 2 | 94,6 | 2 | 101,5 | 1 | ||||
| 64,3 | 1 | 78,1 | 2 | 87,5 | 1 | 94,7 | 1 | 101,9 | 1 | ||||
| 65,5 | 1 | 78,4 | 1 | 87,8 | 1 | 95,7 | 1 | 102,2 | 1 | ||||
| 67,4 | 1 | 78,8 | 1 | 87,9 | 2 | 95,8 | 2 | 102,3 | 1 | ||||
| 67,7 | 1 | 79,0 | 1 | 88,0 | 2 | 95,9 | 1 | 102,7 | 1 | ||||
| 67,8 | 1 | 79,4 | 1 | 88,3 | 1 | 96,0 | 1 | 102,8 | 1 | ||||
| 68,1 | 1 | 80,0 | 2 | 88,6 | 1 | 96,1 | 1 | 103,3 | 1 | ||||
| 68,3 | 1 | 80,4 | 1 | 88,8 | 1 | 96,2 | 1 | 103,4 | 1 | ||||
| 68,9 | 1 | 80,7 | 1 | 88,9 | 2 | 96,3 | 1 | 104,0 | 1 | ||||
| 69,6 | 1 | 80,9 | 2 | 89,2 | 2 | 96,5 | 1 | 104,2 | 1 | ||||
| 69,9 | 1 | 81,3 | 1 | 89,3 | 2 | 96,8 | 1 | 104,4 | 1 | ||||
| 70,5 | 1 | 81,9 | 1 | 89,4 | 1 | 96,9 | 1 | 105,3 | 1 | ||||
| 71,4 | 1 | 82,0 | 2 | 89,7 | 2 | 97,0 | 1 | 105,5 | 1 | ||||
| 72,0 | 2 | 82,1 | 2 | 89,9 | 2 | 97,1 | 1 | 105,6 | 1 | ||||
| 72,1 | 1 | 82,3 | 3 | 90,0 | 1 | 97,5 | 2 | 105,8 | 1 | ||||
| 72,5 | 1 | 82,4 | 1 | 90,2 | 3 | 97,6 | 1 | 106,0 | 1 | ||||
| 72,9 | 1 | 82,8 | 1 | 90,4 | 1 | 97,7 | 1 | 106,2 | 1 | ||||
| 73,7 | 1 | 83,0 | 1 | 90,5 | 1 | 97,8 | 1 | 106,3 | 1 | ||||
| 73,9 | 1 | 83,1 | 1 | 90,6 | 1 | 97,9 | 1 | 108,0 | 1 | ||||
| 74,1 | 1 | 83,4 | 1 | 90,7 | 3 | 98,0 | 1 | 110,0 | 1 | ||||
| 74,8 | 2 | 83,7 | 4 | 91,2 | 1 | 98,2 | 1 | 111,2 | 1 | ||||
| 75,1 | 2 | 83,9 | 2 | 91,3 | 1 | 98,6 | 1 | 112,0 | 1 | ||||
| 75,2 | 1 | 84,6 | 1 | 91,4 | 1 | 98.8 | 1 | 112,2 | 1 |
§ 51. [Ein vergleichender Blick auf diese Tafeln zeigt ebenso bezüglich des Ganges der z wie bezüglich der Aneinanderreihung der a eine wesentliche Verschiedenheit der drei ersten Tafeln von der letzten. Die ersteren besitzen nämlich einen mittleren Hauptbestand, dessen z gegen die Tafelmitte zu im allgemeinen wachsen, und dessen a , von einzelnen Unterbrechungen gegen die Enden zu abgesehen, eine aquidistante Reihe bilden. So erstrecken sich in I. die äquidistanten a in ununterbrochener Folge von 378 bis 428 und von 430 bis 435, während gleichzeitig die z , allerdings mit ständig wiederkehrenden Schwankungen, erst wachsen und dann wieder abnehmen. In II. geht die Reihe der äquidistanten a von 488 bis 550 und setzt sich, nach Unterbrechung durch das fehlende a = 551, von 552 bis 555 fort, während wiederum die z einen ähnlichen Gang zeigen. Tafel III. schließlich zeichnet sich bei entsprechendem Verhalten der z zwischen den Grenzen 64,75 und 78,50 durch eine ungestörte Äquidistanz der a aus. Diesem Hauptbestande schließt sich in jeder der drei Tafeln zu Anfang und zu Ende eine verhältnismäßig geringe Anzahl von a-Werten an, deren Distanzen regellos wechseln, und deren z überwiegend gleich 1 sind: sie stellen Endabteilungen mit zerstreuten a dar. In der vierten Tafel dagegen schreiten die a durchweg in unregelmäßigen Intervallen vor, und es läßt sich nur bemerken, daß die kleineren Intervalle häufiger in der Mitte als an den Enden sich finden; zugleich ist die überwiegende Mehrzahl der z gleich 1. Man kann somit Tafeln, die einen Hauptbestand äquidistanter a neben Endabteilungen mit zerstreuten a besitzen, und solche, deren a durch die ganze Tafel durch unregelmäßig sich zerstreuen, unterscheiden. Als Repräsentanten des ersten Typus haben die Tafeln I. bis III. zu gelten; den zweiten Typus stellt die Tafel IV. dar. Beide Typen sind wesentlich von einander verschieden; denn es wird sich zeigen, daß Tafeln vom zweiten Typus einer viel weiter gehenden Reduktion bedürfen als solche vom ersten, falls ihre Behandlung Erfolg haben soll.]
[Bei der Abgrenzung des Hauptbestandes einer Tafel ist nun aber zu berücksichtigen, daß er sich nicht in scharfer Bestimmtheit von den Endabteilungen loslöst. Man könnte zwar jeder Unbestimmtheit durch Aufstellen der Kegel begegnen, daß der Hauptbestand sich genau so weit erstrecken solle, als die Aquidistanz der a reicht. Es ist jedoch von vornherein klar, daß so keine wesentliche Bestimmung getroffen würde. Denn vielfach kann der Fall eintreten, daß selbst gegen die Mitte der Tafel zu die Äquidistanz durch ein fehlendes a gestört wird; noch häufiger wird von der Mitte aus gegen Anfang oder gegen Ende auf ein fehlendes a nochmals eine Reihe äquidistanter a folgen, wie dies tatsächlich für I und II infolge des Fehlens von a = 429 resp. a = 551 zutrifft. In solchen Fällen würde der Hauptbestand bei Festhalten der obigen Regel entweder übermäßig beschränkt oder völlig in Frage gestellt. Andererseits ist es auch möglich, daß die a zwar lückenlos verlaufen, der Gang der z aber ihre Ausschließung vom Hauptbestande als wünschenswert erscheinen läßt. Es muß daher die Bestimmung des Hauptbestandes innerhalb eines gewissen Spielraumes der Willkür überlassen bleiben, da eine Regel nur insoweit sich aufstellen läßt, daß die Äquidistanz der a -Werte nicht erheblichen Störungen unterworfen und bezüglich der z , wenigstens im ganzen, ein Wachstum gegen die Mitte zu erkennbar sein soll. So kann man denn als Grenzen des Hauptbestandes für I 378 und 435, für II 488 und 555, für III 64,75 und 78,50 festsetzen, mit der Bemerkung jedoch, daß diese Grenzen sehr wohl eine Verschiebung gestatten.]
[Übrigens kann die Äquidistanz der a wenigstens formal auch im Falle fehlender a hergestellt werden, wenn die fehlenden a , mit einem z = 0 versehen, in die Tafel aufgenommen werden. Es soll dies als Einschieben leerer a bezeichnet werden. Beispielsweise wird der Hauptbestand von I und II in dieser Weise durchweg äquidistant, wenn in I 429, in II 551 mit einem z = 0 eingeschoben wird.]
Was ferner den Gang der z im Hauptbestande der Tafeln I – III betrifft, so wurde bereits bemerkt, daß die Zunahme gegen die Mitte zu ständigen Schwankungen unterworfen ist. Nun ist allerdings ein ununterbrochenes Wachsen und Wiederabnehmen schon wegen der nie fehlenden unausgeglichenen Zufälligkeiten gar nicht zu erwarten. Sollte aber hierin allein die Ursache liegen, so bliebe die unverkennbar hervortretende Periodizität in dem Schwanken der z unerklärlich. Es muß daher noch eine andere Ursache zu Grunde liegen. Dieselbe erhellt aus folgenden Bemerkungen.]
[Im Hauptbestande von I treten im ganzen 18 relative Maxima, 17 dazwischen liegende Minima auf; 8 Maxima fallen auf solche a , die ganze oder halbe Zentimeter darstellen, während kein einziges Minimum einem solchen a zugehört. Von den 17 Maxima des Hauptbestandes von II fallen 10, von den 16 Minima keines auf a der bezeichneten Art. Dies zeigt zur Genüge, daß bei der Messung der Schädel mittelst des Bandmaßes, wobei offenbar die Millimeter durch Schätzung gewonnen wurden, ganze und halbe Zentimeter bevorzugt wurden; denn anderenfalls müßten sich der Wahrscheinlichkeit gemäß die Maxima und Minima gleichmäßig auf die Unterabteilungen des Zentimeters verteilen. In der ungleichförmigen Schätzung, d.h. in der Bevorzugung der ganzen und halben Abteilungen des benutzten Maßstabes, findet man somit die Quelle der periodisch wiederkehrenden Unregelmäßigkeiten im Gange der z. Dies bestätigt sich an der Tafel III. Von den 19 Maxima ihres Hauptbestandes fallen 9 auf ganze, 7 auf halbe Zoll; von den 18 Minima gesellen sich nur 2 ganzzolligen Werten zu, während die übrigen ¼ - oder ¾-zolligen Werten zugehören.]
[Man wird sich daher bei der Bearbeitung der Verteilungstafeln vor den Fehlern wegen ungleichförmiger Schätzung zu hüten haben und auf ihre Beseitigung durch eine angemessene Reduktion bedacht sein müssen. Dies führt dazu, die Tafeln, der Periode der ungleichförmigen Schätzung entsprechend, in Hauptabteilungen zu gliedern. Dieselben müssen beispielsweise in den Tafeln I und II von 5 zu 5 mm, in der Tafel III nach halben Zoll oder besser nach ganzen Zoll fortschreiten. Im allgemeinen wird man diese Hauptabteilungen mit dem Hauptbestande der Tafel beginnen lassen. Man kann es dann vorteilhaft finden, den Hauptbestand so zu umgrenzen, daß er gerade eine volle Anzahl von Hauptabteilungen faßt. Dann müssen z. B. in Tafel I drei Werte von dem wie oben definierten Bestande abgeschnitten und etwa die Werte 380 und 434 als Grenzen gewählt werden, zwischen welchen 11 Hauptabteilungen Platz finden, wie in der Tafel selbst angedeutet wurde.]
§ 52. [Schließlich sind noch folgende, für jede Verteilungstafel in ihrem ganzen Umfange gültige Punkte zu erwähnen. Jeder Messung sind Grenzen der Genauigkeit gestellt, so daß die a niemals kontinuierlich sich aneinanderreihen können, sondern durch ein Intervall, dessen Größe von dem Genauigkeitsgrade der Messung abhängt, getrennt verlaufen müssen. Dieses Intervall soll das primäre Intervall heißen und mit i bezeichnet werden. Es ist für die Erstreckung der ganzen Tafel konstant, da es ja nur durch den Maßstab, nicht durch die Größe der gemessenen Gegenstände bedingt wird.]
[In seiner Existenz hat man den Grund dafür zu suchen, daß ein äquidistanter Hauptbestand in den Verteilungstafeln überhaupt möglich ist. Denn das Intervall des Hauptbestandes ist eben nichts anderes als jenes primäre i , das nicht unterschritten werden kann, sondern nur um so deutlicher hervortritt, je größer die Anzahl der gemessenen Exemplare des K.-G. – das m der Tafel – wird. Das primäre i ist aber natürlich auch für Tafeln ohne Hauptbestand aus den a-Werten direkt zu ersehen. Für Tafel IV z. B. ist es gleich dem zehnten Teile von E , d. i. = 0,05 cm.]
[Die wesentliche Bedeutung des Vorhandenseins eines primären Intervalles besteht nun aber darin, daß es die Zugehörigkeit der z zu den a , welchen jene in den Tafeln beigeschrieben werden, in das richtige Licht setzt. Man erkennt nämlich, daß die a bloß als Vertreter der primären Intervalle aufzufassen sind, deren Mitten sie darstellen; es sind darum auch die z nicht als den a , sondern als den durch die a bezeichneten, primären Intervallen zugehörig aufzufassen und innerhalb der letzteren gleichmäßig verteilt zu denken, da es an jedem Anhalte für eine anders gestaltete, gesetzmäßige Verteilung fehlt. Insofern so das primäre Intervall das a umschließt oder umkreist, soll es das Umkreisintervall des a genannt werden. Seine beiderseitigen Grenzen sind a - ½ i und a + ½ i ; dieselben schließen sich durch die ganze Tafel durch unmittelbar aneinander, so daß die erste Grenze eines beliebigen Intervalles mit der zweiten des vorhergehenden zusammenfällt.]
[Die a- und z-Werte sind somit mittelst des zugehörenden Umkreisintervalles aneinander gebunden. Soll diese Verbindung gelöst und das a für sich allein betrachtet und aufgefaßt werden, so soll es als nacktes a bezeichnet werden.]
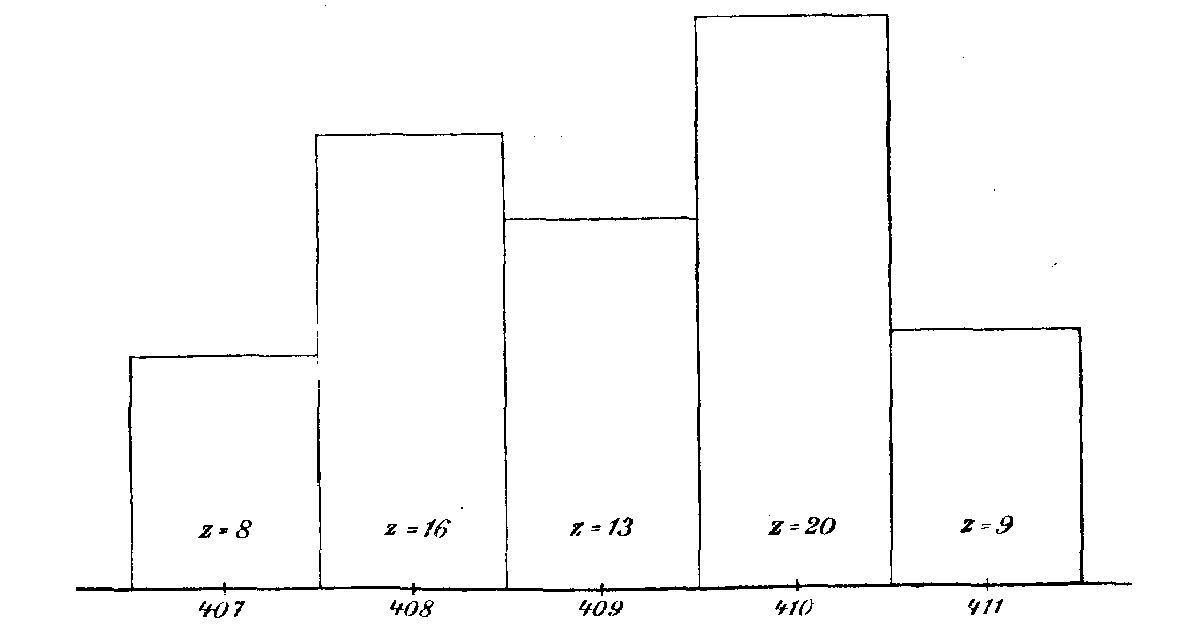
[Die soeben erläuterte Zugehörigkeit der z zu den a gestattet nun auch eine zutreffende geometrische Darstellung der Verteilungstafeln. Es sind nämlich die a in einer Abszissenlinie aufzutragen und durch Markieren der Werte a - ½ i und a + ½ i die Umkreisintervalle derselben beizufügen; sodann sind auf den letzteren Rechtecke zu errichten, deren Inhalte die den a der Tafel beigeschriebenen z repräsentieren müssen; hierbei kann natürlich sowohl der Abmessung der a , als auch der Konstruktion der Rechtecke ein beliebiger Maßstab zu Grunde gelegt werden, da es nur gilt, ein Bild von den Verhältnissen der Tafelwerte zu gewinnen.]
[Man erhält so z. B. folgende Darstellung des mittleren Teiles von Tafel I:]
