Vorliegendes Werk ist schon seit vielen Jahren von mir angelegt, Material dazu gesammelt und in der Ausarbeitung desselben vorgegangen, diese aber vielfach durch andere Arbeiten unterbrochen, längere Zeit ganz beiseite gelegt und somit der Abschluß des Werkes bisher verzögert worden. Ihn länger zu verzögern, möchte bei meinem Alter nicht rätlich sein, wenn das Werk überhaupt erscheinen soll; auch glaube ich wohl, daß es sich nach wiederholtem Zurückkommen darauf endlich getrauen darf, zu erscheinen, zwar nicht als ein vollkommenes Werk, aber als Unterlage für einen weiteren Ausbau der hier behandelten Lehre. Bestimmter spricht sich das folgende Einleitungskapitel über die Aufgabe der Lehre aus; und so mögen hier nur noch folgende allgemeine Bemerkungen darüber Platz finden.
Mit dem neuen Namen, unter dem die Lehre hier auftritt, gebe ich sie doch nicht als eine ganz neue Lehre; nur daß der bisherige Stand ihrer Entwicklung das Bedürfnis noch nicht nahe legte, sie überhaupt unter einem besonderen Namen für sich aufzustellen. Überall spezialisiert sich ja die Wissenschaft im Wege ihrer wachsenden Entwicklung und verlangt demgemäß trennende Bezeichnungen ihrer verschiedenen Gebiete. Nun dürfte das Allgemeinste, Interessanteste, Verdienstlichste, was von unserer Lehre bisher vorlag, in quetelet's "Lettres sur la théorie des probabilités" (1846) und seiner "Physique sociale." (1869) zu finden sein, und wenn man will, kann man in ihm ebenso den Vater der Kollektivmaßlehre, wie in E. H. weber den der Psychophysik sehen; doch wird man sich aus dem Verfolg dieses Werkes überzeugen können, wieviel Anlaß doch war, nicht nur wesentlich erweiternd, sondern auch berichtigend über ihn hinauszugehen.
In dieser Beziehung mache ich von einer Seite als Hauptfrucht, von anderer als Hauptwur-zel der ganzen folgenden Untersuchung die sich gegenseits kontrollierende mathematische Begründung und empirische Bewährung einer Verallgemeinerung des GAUSS'schen Gesetzes zufälliger Abweichungen geltend, wodurch die Beschränkung desselben auf symmetrische Wahrscheinlichkeit und verhältnismäßige Kleinheit der beiderseitigen Abweichungen vom arithmetischen Mittel gehoben wird, und bisher unbekannte gesetzliche Beziehungen auftreten, deren wichtigste man § 33 zusammengestellt findet. In der Tat ist in dieser Verallgemeinerung der allgemeinste Regulator aller in der Kollektivmaßlehre zur Sprache kommenden Verhältnisse ebenso gegeben, als im einfachen GAUSS'schen Gesetze der Regulator aller physikalischen und astronomischen Genauigkeitsbestimmungen, und dürfte sich selbst noch fragen, ob nicht prinzipiell auch hier auf das allgemeinere Gesetz zu rekurrieren wäre, worüber man die Bemerkungen in § 8 nicht unberücksichtigt lassen möge.
Insofern die Kollektivmaßlehre auf einer Verbindung von Beobachtung- und Rechnung in gegenseitiger Beziehung beruht, darf sie sich zu den exakten Lehren rechnen. Die Lehren, die auf eine solche Bezeichnung Anspruch haben, lassen aber überhaupt einen sehr verschiedenen Grad der Sicherheit ihrer Resultate zu. Obenan stehen Mechanik, Astronomie, Physik; die Physiologie steht wegen der Schwierigkeiten, welche die Komplikation und Variabilität ihrer Objekte entgegenstellen, weit dahinter zurück; noch weiter, wegen noch größerer Schwierigkeiten in dieser Hinsicht, die Psychophysik. Die Kollektivmaßlehre teilt Schwierigkeiten dieser Art, ohne gleichen prinzipiellen Schwierigkeiten zu unterliegen als die Psychophysik, überbietet diese an praktischem Interesse, indes sie ihr an philosophischem Interesse weit nachsteht. Doch fehlt es auch der Kollektivmaßlehre nicht ganz an einem solchen, sofern die darein eingehende Unterordnung des Zufalls unter allgemeinere Gesetze hier in einem Gebiete und in einer Weise zur Geltung kommt, welche bisher der Betrachtung nicht unterlegen haben.
In betreff der Form und Weite so mancher Ausführungen wird zu berücksichtigen sein, daß das Werk nicht sowohl für Fachmathematiker bestimmt ist, denen die hier in Rücksicht kommenden fundamentalen Punkte schon geläufig sind, als für solche, denen es um Kenntnisnahme und Anwendung der Lehre zu tun ist, ohne daß sie schon im Besitz solcher Vorkenntnisse sind.
Hiernächst möchte ich zur Förderung unserer Lehre noch einen Wunsch an Rechner vom Fach richten. In den bekannten Tabellen, welche das GAUSS'sche Wahrscheinlichkeitsintegral der zufälligen Abweichungen vom Mittel (Beobachtungsfehler) gewöhnlich als
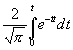
ausgedrückt darstellen, ist das Argument t bloß bis auf zwei Dezimalen ausgeführt, was für den beschränkten Gebrauch, den Physiker und Astronomen davon zu machen haben, unter Zuziehung einer Interpolation mit ersten und zweiten Differenzen ausreicht; aber für den weit ausgedehnteren Gebrauch, der in der Kollektivmaßlehre davon zu machen ist, auf dasselbe herauskommt, als wenn man für die vielen Rechnungen, die mittelst Logarithmen zu führen sind, das Zahlenargument, wozu die Logarithmen gehören, bloß auf zwei oder drei Ziffern reduzieren und Zwischenbestimmungen nur der Interpolation anheimgeben wollte. Also wäre erwünscht, wenn im Interesse unserer Lehre, was übrigens von der psychophysischen Methode der richtigen und falschen Fälle geteilt wird, Tabellen vorlägen, worin t mindestens auf vier Dezimalen ausgeführt ist 1), um Interpolationen teils zu ersparen, teils zu erleichtern, und jedenfalls habe ich selbst solche Tabellen bei Ausführung dieser Arbeit schmerzlich vermißt. Natürlich würde die Ausdehnung der Tabellen damit wachsen, aber der Vorteil schien mir in stärkerem Verhältnisse damit zu wachsen. Und sollte es denn kein astronomisches oder statistisches Institut geben, was über mechanische Rechenkräfte zu verfügen hat, das sich der Sache annähme! Auch ließe sich wohl eine Preisaufgabe darauf stellen.
1 ) Eine Ausführung dieser Tabelle
auf drei Dezimalen von t, mit Beschränkung des Integralwertes
auf vier resp. fünf Dezimalen, findet man im Anhang § 183.