V.

Die Schnelligkeit des Lernens von Silbenreihen
als Funktion der Länge derselben.

§ 19. Versuche der späteren Periode.

    Es ist hinreichend bekannt, dass die Einprägung von Vorstellungsreihen, die zu einer bestimmten späteren Zeit reproduziert werden sollen, um so schwieriger ist, je länger die Reihen sind. Das heißt, diese Einprägung erfordert nicht nur absolut genommen mehr Zeit bei größerer Länge der Reihen, weil eben jede Wiederholung länger dauert, sondern sie beansprucht auch verhältnismäßig mehr Zeit, weil eine wachsende Anzahl von Wiederholungen nötig wird. Sechs Verse eines Gedichtes kosten, um gelernt zu werden, nicht nur dreimal soviel Zeit wie zwei, sondern erheblich mehr.
    Ich habe dieses Abhängigkeitsverhältnis, welches sich natürlich auch bei der ebenmöglichen Reproduktion sinnloser Silbenreihen geltend macht, nicht eigens untersucht, aber beiläufig dafür einige Zahlen gewonnen, die, ohne besonders interessante Beziehungen darzubieten, immerhin der Mitteilung wert sind.
    Die in Betracht gezogenen Reihen umfaßten (bei den Versuchen der Jahre 1883/84) je 12, 16, 24 oder 36 Silben, und zwar waren hierbei je 9, 6, 3 oder 2 Reihen jedesmal zu einem Versuch zusammengefaßt.
    Für die Anzahl von Wiederholungen, welche in diesen Fällen nötig waren, um die Reihen bis zur ersten fehlerfreien Reproduktion (diese mitgerechnet) zu lernen, fanden sich folgende Zahlen:
 

x Reihen
zu je y Silben
erforderten zusammen durchschnittlich z Wiederholungen
Wahrscheinlicher Fehler der Durchschnittswerte
Zahl der Versuche
x =
y =
z =
9
12
158
± 3,4
7
6
16
186
± 0,9
42
3
24
134
± 2,9
7
2
36
112
± 4
7

    Um die Anzahl der Wiederholungen vergleichbarer zu machen, muß man sie, sozusagen, auf einen Generalnenner bringen und jedesmal durch die Zahl der Reihen dividieren. Man erfährt so, wieviel Wiederholungen verhältnismäßig nötig waren, um einzelne Reihen gerade auswendig zu lernen, die sich nur durch die Zahl der Silben von einander unterschieden und jedesmal mit soviel anderen derselben Art zusammengenommen waren, dass die Dauer des ganzen Versuchs 15–30 Minuten betrug1).

1) Man könnte einwenden, dass durch diese Division auf die Durchschnittswerte für das Lernen der einzelnen Reihen zurückgegriffen und dass damit das Resultat des vierten Abschnittes außer Acht gelassen würde. Denn nach diesem durften zur Ermittelung von Abhängigkeitsbeziehungen zwar die Mittelwerte aus den für Reihengruppen aber nicht aus den für einzelne Reihen erhaltenen Zahlen verwandt werden. Allein es wird gar nicht behauptet, dass die oben durch Division zu gewinnenden Zahlen richtige Durchschnittswerte für die den einzelnen Reihen zukommenden Zahlen bildeten, d. h. dass letztere sich gemäß dem Fehlergesetz um sie gruppieren. Sondern die Zahlen sind als Durchschnittszahlen für Reihengruppen zu betrachten, bei denen nur zur besseren Vergleichung mit anderen ein Umstand, der der Natur der Sache nach nicht überall derselbe sein konnte, durch Division ausgeglichen ist. Der ihre Sicherheit messende wahrscheinliche Fehler ist nicht aus den Zahlen für die Einzelreihen, sondern aus denen für die Reihengruppen berechnet.     Außerdem aber kann man den Zahlen nach der Seite der abnehmenden Silben einen Abschluß geben. Man kann fragen: wie groß ist diejenige Zahl von Silben, welche unmittelbar nach einmaligem Durchlesen derselben gerade noch fehlerlos hergesagt werden kann? Für mich beträgt diese Anzahl ziemlich genau 7 Silben. Es gelingt zwar auch oft, 8 Silben wiederzugeben, aber nur zu Anfang der betreffenden Versuche und im ganzen in der großen Minorität der Fälle. Bei 6 Silben andererseits kommt sozusagen nie ein Fehler vor; bei ihnen ist also ein aufmerksames einmaliges Durchlesen schon zuviel Energieentfaltung für eine unmittelbar darauf folgende Reproduktion.
    Fügt man also dieses letztere Größenpaar hinzu, vollzieht die eben geforderte Division und bringt endlich die Wiederholung, die in dem letzten fehlerfreien Hersagen besteht, also nicht mehr auf das Lernen verwandt wurde, in Abzug, so ergibt sich folgende Tabelle.
 
Anzahl der Silben einer Reihe Anzahl der bis zum ersten fehlerfreien Hersagen (excl.) erforderlichen Wiederholungen Wahrscheinlicher Fehler
7
1
12
16,6
± 1,1
16
30
± 0,4
24
44
± 1,7
26
55
± 2,8

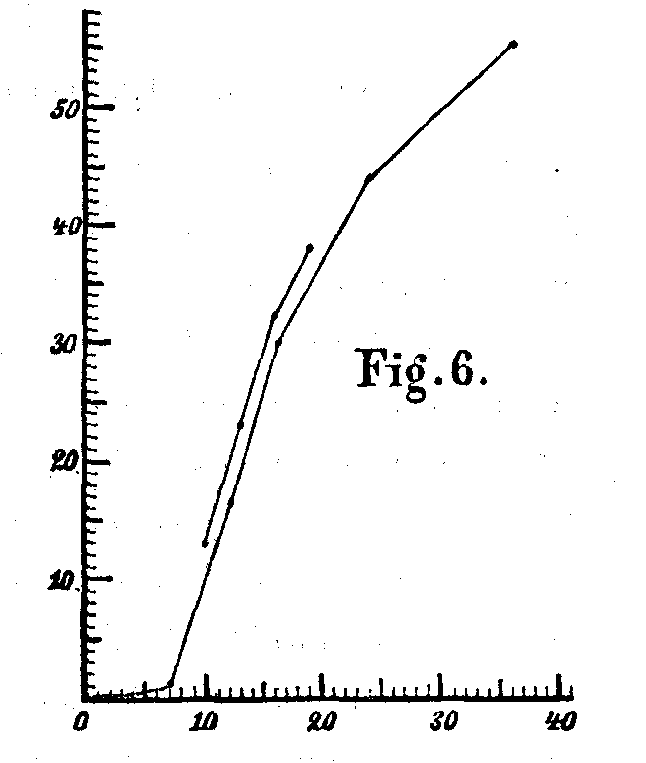
    Den regelmäßigen Gang dieser – für die geringe Zahl der Versuche ziemlich sicheren – Zahlen veranschaulicht die größere der nebenstehenden beiden Kurven. Wie sie zeigt, wuchs in den untersuchten Fällen die Anzahl der Wiederholungen, die für das Lernen von Reihen mit zunehmend größerer Silbenzahl nötig waren, außerordentlich schnell mit der Zunahme der Silben. Namentlich zuerst ist der Anstieg der Kurve ein sehr steiler, weiterhin scheint er sich allmählich zu verflachen. Zur Bewältigung des Fünffachen von derjenigen Silbenzahl, die gerade noch nach einmaligem Durchlesen (d. h. etwa nach 3 Sekunden) reproduziert werden konnte, waren über 50 Wiederholungen notwendig, welche die ununterbrochene und anstrengende Arbeit einer Viertelstunde in Anspruch nahmen.

    Die Kurve hat ihren natürlichen Ausgangspunkt im Nullpunkt der Koordinaten. Das kurze Anfangsstückchen bis zu dem Punkt x = 7, y = l kann man so deuten: um Reihen von 6, 5, 4 u. s. w. Silben auswendig hersagen zu können, ist natürlich immer ein einmaliges Durchlesen derselben erforderlich, aber dasselbe braucht (für mich) nicht, wie bei 7 Silben, mit möglichst gespannter Aufmerksamkeit zu geschehen, sondern kann immer flüchtiger sein, um je weniger Silben es sich handelt.

§ 20. Versuche der früheren Periode.

    Selbstverständlich haben die mitgeteilten – an einem einzigen Individuum gewonnenen Zahlen – auch nur für dieses eine Individuum Bedeutung. Es fragt sich, ob sie nun auch wenigstens für dieses Individuum von genereller Bedeutung sind, also bei Wiederholung der Versuche zu anderen Zeiten in annähernd ähnlicher Größe und Gruppierung wieder erwartet werden dürfen oder nicht.
    Eine Reihe von Versuchsresultaten der älteren Periode gibt die erwünschte Möglichkeit einer Kontrolle in dieser Richtung. Dieselben sind wiederum beiläufig gewonnen (also unbeeinflußt durch Erwartungen und Voraussetzungen), und zwar aus Versuchen, die unter etwas anderen Umständen angestellt sind als die eben mitgeteilten. Die Tageszeit war eine frühere, außerdem wurde das Lernen fortgesetzt, bis die einzelne Reihe zwei Mal hintereinander ohne Fehler hergesagt werden konnte. Ein Versuch umfaßte
        15 Reihen von je 10 Silben
oder   8 "          "     "   13 "
"         6 "          "    "    16 "
"         4 "          "    "    19 "
    Es sind also wiederum 4 verschiedene Reihenlängen in Betracht gezogen, dieselben liegen aber auf einer viel kürzeren Strecke zusammengedrängt.
    Da die Wiederholungen – auf die es hier ankommt – in der älteren Periode überhaupt nicht gezählt wurden, so mußte ihre Anzahl aus den Zeiten berechnet werden. Dazu ist die oben (§ 15) mitgeteilte Tabelle, nach entsprechender Interpolation, benutzt worden. Werden die gefundenen Zahlen gleich auf je eine Reihe reduziert und dabei die beiden Wiederholungen, welche das Hersagen ausmachen, wie oben, abgezogen, so ergibt sich:
 

Anzahl der Silben einer Reihe
Anzahl der bis zu zweimaligem fehlerfreien Hersagen (excl.) erforderlichen Wiederholungen
Wahrscheinlicher Fehler2)
Anzahl der Versuche
10
13
± l
16
13
23
± 0,5
92
16
32
± 1,2
6
19
38
± 2
11
2) Die wahrscheinlichen Fehler beruhen ebenfalls auf Umrechnung und haben nur einen ungefähr orientierenden Wert.     Die kleinere Kurve der obigen Fig. 6 veranschaulicht graphisch die Lage dieser Zahlen. Wie man sieht, war für gleichlange Reihen die Anzahl der für das Auswendiglernen nötigen Wiederholungen in der älteren Zeit überall etwas größer als in der späteren. Eben wegen seiner Gleichförmigkeit wird dieses Verhalten in der Verschiedenheit der Versuchsumstände, in den Ungenauigkeiten der Umrechnung, vielleicht auch in der gesteigerten Übung der späteren Periode seinen Grund haben. Immerhin fallen die älteren Zahlen sehr annähernd in die Gegend der jüngeren, und – was die Hauptsache ist – die beiden sie darstellenden Kurven schmiegen sich, auf der allerdings kurzen Strecke ihres gemeinsamen Verlaufs, so vollkommen aneinander an, wie man es für Versuche, die durch ca. 31/2 Jahre voneinander getrennt sind und ganz sicher keiner Trübung durch irgend welche Erwartung unterlagen (§ 14), nur immer wünschen kann. Man wird also mit erheblicher Wahrscheinlichkeit behaupten dürfen, dass das durch jene Kurven dargestellte Abhängigkeitsverhältnis zwar nur individuell ist, aber für das eine Individuum, an dem es gefunden wurde, über größere Zeiten hinweg konstant bleibt und deshalb für dieses charakteristische Bedeutung besitzt.

§ 21. Steigerung der Schnelligkeit des Lernens bei sinnvollem Material.

    Um auf die Gleichförmigkeiten und Verschiedenheiten zwischen sinnlosem und sinnvollem Material aufmerksam zu werden, habe ich gelegentlich, wie schon erwähnt, Lernversuche mit Byrons Don Juan (mit dem englischen Original) angestellt. Dieselben gehören insofern nicht eigentlich hierher, als ich bei ihnen die Länge des jedesmal zusammengefaßten Quantums nicht variiert habe, sondern immer nur einzelne Stanzen auswendig lernte. Indes die Angabe der hierzu erforderlich gewesenen Anzahl von Wiederholungen ist durch ihren Kontrast mit den eben mitgeteilten Zahlen auch an und für sich interessant.
    In Betracht kommen nur 7 Versuche (1884), deren jeder 6 Stanzen umfaßte. Wurden diese, jede für sich, bis zur erstmöglichen Reproduktion gelernt, so waren für alle 6 zusammen durchschnittlich 52 Wiederholungen (wm = ± 0,6) nötig. Für jede Stanze ergibt das knapp 9, oder, nach Abzug der Wiederholung für das Hersagen, knapp 8 Wiederholungen3). Erwägt man, dass jede Stanze 80 Silben umfaßt, (die allerdings durchschnittlich etwas weniger als 3 Buchstaben zählen dürften), so gewinnt man durch Vergleichung der jetzt gefundenen Zahl von Wiederholungen mit den obigen einen wenigstens ungefähren numerischen Ausdruck für die außerordentliche Begünstigung, welche der Einprägung von Reihen durch die vereinigten Bande des Sinnes, des Rhythmus, des Reims und der Zugehörigkeit zu einer einzigen Sprache zu Teil wird. Denkt man sich unsere obige Kurve in der Krümmung, die sie einzuschlagen scheint, noch eine Strecke fortgeführt, so muß man voraussetzen, dass ich sinnlose Reihen von 70–80 Silben nach 70–80maliger Wiederholung auswendig hersagen könnte. Waren die Silben durch die eben erwähnten Fäden äußerlich und innerlich aneinander gekettet, so reduzierte sich also dieses Erfordernis für mich auf etwa 1/10 seines Betrages.

3) Zur richtigen Würdigung der Zahlen und zum richtigen Anschluß an etwaige eigene Beobachtungen wolle man das im § 12 Gesagte beachten. Die Stanzen wurden, der Gleichförmigkeit des Verfahrens halber, immer von Anfang bis zu Ende durchgelesen; schwierigere Stellen wurden also nicht etwa besonders gelernt und dann eingefügt. Geschah das letztere, so fielen die Zeiten erheblich geringer aus; von der Anzahl von Wiederholungen kann man dann nicht mehr sprechen. Natürlich geschah das Lesen zwar möglichst mit gleichförmiger Schnelligkeit, aber nicht in dem langsamen und mechanisch geregelten Tempo, welches für die Silbenreihen festgesetzt war. Die Regelung der Geschwindigkeit war der freien Schätzung überlassen; einmaliges Durchlesen einer Stanze erforderte 20–23 Sekunden.